Origin FFT优化秘籍：5大参数调整技巧，提升频谱分析至极致


参考资源链接：[Origin软件快速傅里叶变换(FFT)实操教程](https://wenku.csdn.net/doc/f4sz0rt6pp?spm=1055.2635.3001.10343)
# 1. 频谱分析与FFT的理论基础

频谱分析是研究信号频率成分的科学方法，在许多电子和通信系统中扮演着关键角色。快速傅里叶变换（FFT）是实现频谱分析的一种高效算法，它基于离散傅里叶变换（DFT）原理，通过减少计算量来提升运算速度。本章节将对FFT的理论基础进行浅显易懂的介绍，奠定理解后续章节中更深层次内容的基础。

## 2.1 离散傅里叶变换（DFT）概述

### 2.1.1 DFT的基本定义和数学模型

离散傅里叶变换是一种将时域中的离散信号转换为频域的方法。给定一个N点的复数序列 \(x[n]\)，DFT定义为：

\[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j2\pi nk/N} \]

其中 \(X[k]\) 是复数频域表示，\(j\) 是虚数单位，\(e\) 是自然对数的底，\(k\) 是频率索引（\(k = 0, 1, \ldots, N-1\)）。

### 2.1.2 DFT的核心运算过程

DFT的核心是通过复数的加权和来计算频谱。这一过程涉及了大量的复数乘法和加法运算，对于长序列来说计算量很大。具体而言，每次计算一个频率分量需要 \(N\) 次复数乘法和 \(N-1\) 次复数加法，整个DFT需要 \(N^2\) 次这样的操作。

## 2.2 快速傅里叶变换（FFT）的出现

### 2.2.1 Cooley-Tukey算法的诞生与发展

为了提高DFT的运算效率，Cooley和Tukey在1965年提出了快速傅里叶变换FFT算法。这个算法采用分治策略，将长序列分解为短序列，然后递归地应用DFT。FFT的发展大大降低了频谱分析的计算复杂度，使得实时处理信号变得可能。

### 2.2.2 FFT算法的提速原理

FFT算法的核心提速原理在于它减少了复数乘法的次数。Cooley-Tukey算法利用了对称性和周期性，将 \(N\) 点DFT拆分成两个 \(\frac{N}{2}\) 点DFT，再通过“蝴蝶”运算逐步合并结果。在理想情况下，一个 \(N\) 点的FFT的复杂度可以降低到 \(\frac{N}{2}\log_2N\) 次复数乘法。

## 2.3 FFT与其他频谱分析方法的比较

### 2.3.1 FFT相对于DFT的优势

相较于DFT，FFT显著减少了必要的计算次数，从而降低了执行时间和资源消耗。举例来说，对于1024点序列，FFT相比于DFT能减少约100倍的计算量。

### 2.3.2 FFT与STFT、WT的对比分析

快速傅里叶变换是频谱分析中应用最广泛的算法之一，但它并不是唯一的算法。短时傅里叶变换（STFT）和小波变换（WT）是另外两种分析时间-频率特性的方法。FFT由于其计算高效性，在实时性要求较高的应用场景中更受欢迎，而STFT和WT提供了对信号时频特征更为精细的分析，但计算开销也相对较大。

通过本章的介绍，我们理解了FFT的基础理论以及它与其它频谱分析方法的比较，为后续章节深入探讨FFT的工作原理和优化技巧打下了坚实的基础。

# 2. FFT算法的工作原理

### 2.1 离散傅里叶变换（DFT）概述

#### 2.1.1 DFT的基本定义和数学模型

离散傅里叶变换（Discrete Fourier Transform，DFT）是将一个离散信号从时域转换到频域的数学工具。它在数字信号处理中扮演着核心角色，是分析信号频率成分不可或缺的方法。DFT可以看作是对连续傅里叶变换（Continuous Fourier Transform，CFT）的一种离散化近似。对于一个长度为N的复数序列\(x[n]\)，其DFT定义如下：

\[X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j \frac{2\pi}{N} nk}\]

其中，\(X[k]\)是复数序列\(x[n]\)的频域表示，\(j\)是虚数单位，\(e\)是自然对数的底数，而\(k\)是频率索引，范围是\(0\)到\(N-1\)。

在实际应用中，DFT的计算量与\(N^2\)成正比，这使得对于较大序列的DFT运算非常耗时。因此，快速傅里叶变换（FFT）应运而生，它将DFT的计算复杂度降低到了\(Nlog_2N\)。

#### 2.1.2 DFT的核心运算过程

DFT的核心运算过程可以视为一系列的加权求和，这些权重是复数指数函数的值。在复平面上，这相当于将序列中的每个点旋转特定的角度后叠加。为了更直观地理解DFT的工作原理，我们可以将其分解为以下几个步骤：

1. 首先确定\(x[n]\)序列的长度N。
2. 对于每一个频率索引\(k\)，计算复指数\(e^{-j \frac{2\pi}{N} nk}\)的值。
3. 将复指数与原序列\(x[n]\)相乘，得到一个临时序列。
4. 对临时序列求和，得到\(X[k]\)的第\(k\)个元素。

重复上述步骤，直到完成所有频率索引\(k\)的计算，得到完整的\(X[k]\)序列。

### 2.2 快速傅里叶变换（FFT）的出现

#### 2.2.1 Cooley-Tukey算法的诞生与发展

快速傅里叶变换（FFT）算法的诞生极大地推动了数字信号处理技术的发展。最著名的FFT算法之一是Cooley-Tukey算法，由J.W. Cooley和J.W. Tukey在1965年提出。该算法基于一个重要的发现：当DFT的序列长度\(N\)是2的幂时，DFT可以被高效地分解成更小的DFT。

Cooley-Tukey算法的核心思想是将一个大DFT分解为若干个较小DFT的组合。具体来说，Cooley-Tukey FFT算法通过蝶形运算实现了分治策略，该策略将\(N\)点的DFT分为两个\(N/2\)点的DFT，然后进行必要的乘法运算以得到最终结果。这一过程可以递归地应用到每个较小的DFT上，直至分解成最简单的情况。

#### 2.2.2 FFT算法的提速原理

Cooley-Tukey FFT算法之所以能够提速，关键在于它减少了重复计算的次数，并且通过蝶形运算实现了数据的高效重用。这里，蝶形运算指的是一个对复数对进行的运算，该复数对由相邻的两个复数构成，并且需要进行一次复数加法和一次复数减法。

在FFT算法中，通过合理的数据排列，可以保证每个中间结果能够被多次利用，避免了重复计算。举例来说，计算一个\(N=8\)的DFT，传统方法需要进行\(8^2=64\)次复数乘法和\(8^2-1=63\)次加法，而通过FFT算法，计算次数可以减少到\(8log_2(8)=24\)次复数乘法和\(24+8=32\)次复数加法。

### 2.3 FFT与其他频谱分析方法的比较

#### 2.3.1 FFT相对于DFT的优势

FFT算法相比DFT的主要优势在于其计算效率。具体来说，FFT算法的速度提升主要体现在以下几个方面：

1. **计算复杂度的降低**：FFT算法将DFT的计算复杂度从\(N^2\)降低到\(Nlog_2N\)，这意味着当\(N\)较大时，FFT的速度会有显著提升。
2. **优化后的存储需求**：由于FFT算法通常采用原地计算（in-place computation），这减少了对额外存储空间的需求。
3. **适合硬件实现**：由于其高效性和规整性，FFT算法特别适合使用专用硬件实现，从而进一步提升处理速度。

#### 2.3.2 FFT与STFT、WT的对比分析

除了FFT之外，短时傅里叶变换（Short-Time Fourier Transform，STFT）和小波变换（Wavelet Transform，WT）也是频谱分析中常用的工具。

STFT通过将信号分割成较短的片段，并对每个片段单独进行傅里叶变换，从而获得信号在不同时间点的频率信息。STFT适用于分析具有时间-频率局部性的信号，但它在时频分辨率之间存在权衡。

WT是另一种时频分析工具，它通过在不同尺度上分析信号，能够提供比STFT更高的时频分辨率。小波变换尤其适用于分析那些突发或者非平稳的信号，但其计算复杂度比FFT更高。

在实际应用中，FFT因其计算效率和实现简单的优势被广泛采用，尤其是在需要实时处理的场合。而STFT和WT则适用于对信号特性有更精细分析要求的场景。

# 3. FFT优化参数调整技巧

在频谱分析中，对快速傅里叶变换（FFT）的参数进行优化是至关重要的。合理的参数调整可以提高分析的准确性与效率，同时避免不必要的计算负荷。本章将深入探讨窗函数的选择、零填充的应用以及分辨率与重叠率权衡等优化技巧。

### 3.1 窗函数的选择与应用

在进行FFT分析时，选择合适的窗函数是提升频谱分析结果质量的关键步骤之一。窗函数的目的是减少由于截断信号导致的频谱泄露（spectral leakage），从而更准确地表示信号的频率特性。

#### 3.1.1 常见窗函数的特性和应用场景

- **矩形窗（Rectangular Window）**：也称为矩形窗或直接窗，是最简单的窗函数。它适用于信号已经预先进行过截断处理或者在信号的开始和结束处没有突变的场景。矩形窗的主瓣宽度最窄，但旁瓣（side lobe）水平最高，因此可能导致较严重的频谱泄露。

- **汉宁窗（Hanning Window）**：相比于矩形窗，汉宁窗可以有效降低旁瓣水平，减少频谱泄露，但代价是主瓣宽度的增加。它适用于一般信号的频谱分析，特别是在对频谱泄露有严格要求的场合。

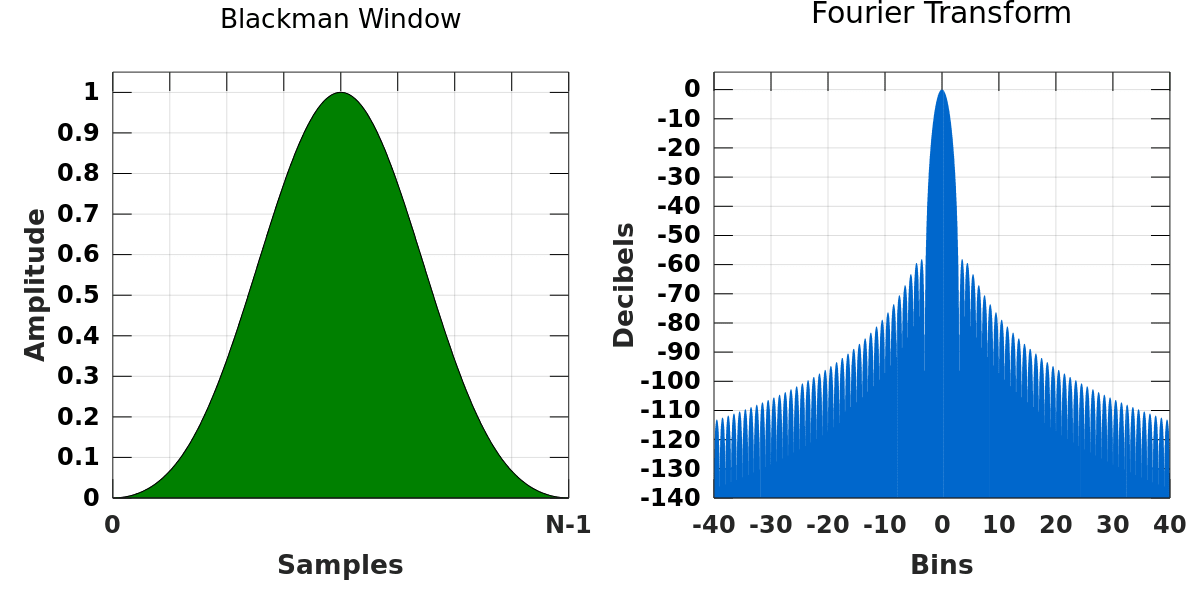
- **布莱克曼窗（Blackman Window）**：此窗函数进一步降低了旁瓣水平，提供了更平滑的主瓣，但主瓣宽度更宽。适用于要求极低频谱泄露的分析，如高精度频率分析。

- **凯泽窗（Kaiser Window）**：凯泽窗是一种参数化的窗函数，可以根据不同的旁瓣抑制要求调整参数。在提供灵活旁瓣水平的同时，保持相对较好的主瓣特性。适用于对分析精度有特定要求的场合。

#### 3.1.2 窗函数对频谱分析结果的影响

选择合适的窗函数可以显著改善FFT结果的质量。例如，使用汉宁窗替代矩形窗进行FFT，能够有效降低频谱泄露，提高频率分量的可分辨性。

**代码示例：使用Python实现不同窗函数的FFT分析**

import numpy as np
from scipy.fft import fft, fftfreq
import matplotlib.pyplot as plt

# 生成测试信号
fs = 1000  # 采样频率
t = np.arange(0, 1, 1/fs)  # 时间向量
f = 5  # 信号频率
signal = np.sin(2 * np.pi * f * t)

# 应用不同的窗函数
windows = ['boxcar', 'hann', 'blackman', 'kaiser']
fig, axs = plt.subplots(len(windows), 1, figsize=(8, 12))
for i, window in enumerate(windows):
    win = getattr(np, window)(len(signal))  # 获取窗函数
    yf = fft(signal * win)  # 应用窗函数并进行FFT
    xf = fftfreq(len(signal), 1/fs)  # 频率向量
    axs[i].plot(xf, np.abs(yf))
    axs[i].set_title(f'Window Function: {window.title()}')

plt.show()

以上代码首先生成一个简单的正弦波信号，然后分别应用四种不同的窗函数进行FFT处理，并绘制其幅度谱。通过对比可以看出不同的窗函数对频谱分析结果的影响。

### 3.2 零填充（Zero-padding）的影响

在FFT的上下文中，零填充指的是在信号序列的末尾添加零值，以扩展信号的长度。这在很多情况下是优化FFT分析的一个重要步骤。

#### 3.2.1 零填充的基本概念

零填充可以增加信号的采样点数，这直接影响FFT分析的频率分辨率。频率分辨率是信号中能够分辨的最小频率差异，其计算公式为：`Fs / N`，其中`Fs`是采样频率，`N`是信号的总点数（包括零填充的零点）。因此，零填充使得频率分辨率