【Python数据结构与图形算法】：数据如何在图形中流动

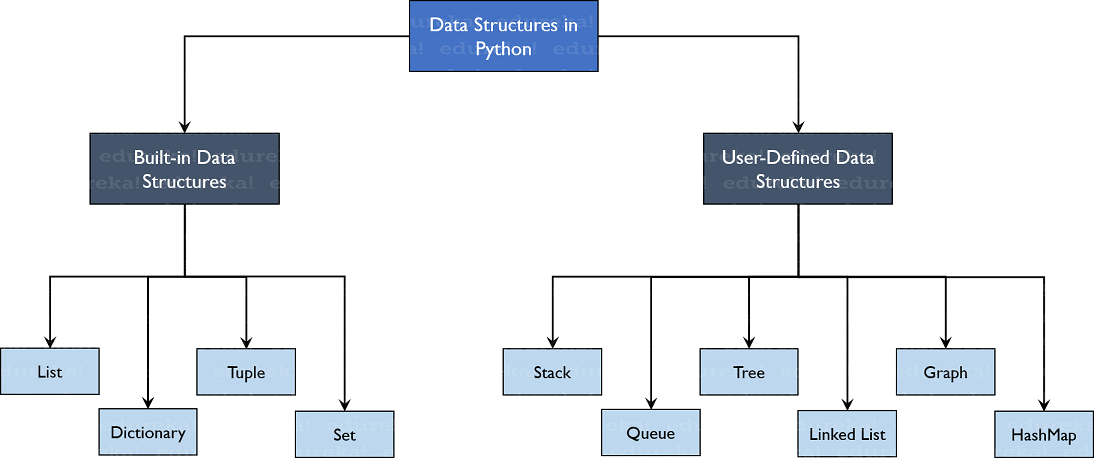
# 1. 数据结构与图形算法概述

在信息技术飞速发展的今天，数据结构和图形算法成为了计算机科学领域的重要基石。数据结构提供了组织和存储数据的多样化方式，是实现高效算法的关键。而图形算法作为数据结构的一种表现形式，广泛应用于社交网络分析、推荐系统、搜索引擎优化等诸多场景。本章节将为读者提供对数据结构与图形算法的基本理解，并探讨二者之间的紧密联系，为后续章节的深入分析打下坚实的基础。

# 2. 基础数据结构及其在图形中的应用

## 2.1 链表和图的遍历

### 2.1.1 链表的实现与基本操作

链表是一种常见的数据结构，它由一系列节点组成，每个节点包含数据本身以及指向下一个节点的指针。在图形算法中，链表常用于表示图的边和顶点信息。以下是链表的基本实现和操作。

首先，我们定义一个节点类（Node）和一个链表类（LinkedList）：

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedList:
    def __init__(self):
        self.head = None

    def append(self, data):
        if not self.head:
            self.head = Node(data)
        else:
            current = self.head
            while current.next:
                current = current.next
            current.next = Node(data)
    def print_list(self):
        current = self.head
        while current:
            print(current.data, end=" -> ")
            current = current.next
        print("None")

在上述代码中，我们首先定义了一个节点类`Node`，它有两个属性：`data`和`next`。`data`存储节点的数据，`next`存储指向下一个节点的指针。然后我们定义了一个链表类`LinkedList`，它有一个属性`head`，表示链表的头节点。

`LinkedList`类中有两个方法：`append`用于在链表的末尾添加新节点，`print_list`用于打印链表中的所有元素直到结束标记`None`。

### 2.1.2 图的深度优先搜索（DFS）

深度优先搜索（DFS）是图遍历算法之一，它从一个节点开始，尽可能深地搜索图的分支。当节点v的所有边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这个过程一直进行到已发现从源节点可达的所有节点为止。

下面是一个图的深度优先搜索实现：

class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.adj = [[] for _ in range(vertices)]

    def add_edge(self, v, w):
        self.adj[v].append(w)

    def DFSUtil(self, v, visited):
        visited[v] = True
        print(v, end=' ')

        for i in self.adj[v]:
            if not visited[i]:
                self.DFSUtil(i, visited)
    def DFS(self, v):
        visited = [False] * self.V
        self.DFSUtil(v, visited)

# 创建一个图实例
g = Graph(4)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
g.add_edge(3, 3)

print("Following is Depth First Traversal (starting from vertex 2)")
g.DFS(2)

在上面的`Graph`类中，我们定义了一个图，其中包含一个顶点数组和一个邻接表`adj`来存储图中的边。`add_edge`函数用于添加边，而`DFS`函数使用深度优先搜索遍历图。

### 2.1.3 图的广度优先搜索（BFS）

广度优先搜索（BFS）是另一种图遍历算法，它从一个节点开始，逐层向外扩展直到所有节点都被访问。算法使用队列数据结构来维护访问过的节点序列。

下面是图的广度优先搜索实现：

from collections import deque

class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.adj = [[] for _ in range(vertices)]

    def add_edge(self, v, w):
        self.adj[v].append(w)

    def BFS(self, s):
        visited = [False] * self.V
        queue = deque()
        visited[s] = True
        queue.append(s)

        while queue:
            s = queue.popleft()
            print(s, end=" ")
            for i in self.adj[s]:
                if not visited[i]:
                    visited[i] = True
                    queue.append(i)

# 创建一个图实例
g = Graph(4)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
g.add_edge(3, 3)

print("Following is Breadth First Traversal (starting from vertex 2)")
g.BFS(2)

在这段代码中，我们使用了Python的`collections.deque`来实现队列功能。`BFS`函数从给定的起始节点开始，使用一个队列来跟踪待访问的节点，并通过一个访问数组`visited`来避免重复访问。

以上就是本章节的第二部分的介绍，我们接下来将深入了解栈和队列在图算法中的运用。

# 3. 高级数据结构与图算法实践

## 3.1 哈希表在图形数据处理中的应用

### 3.1.1 哈希表的原理与实现

哈希表是一种以键值对（key-value pair）为存储形式的数据结构，它通过哈希函数将键映射到存储位置，以实现快速的数据查找、插入和删除操作。哈希表的平均时间复杂度为O(1)，在图形数据处理中应用广泛，尤其是在需要频繁进行查找的场景，如图的搜索、节点映射、以及图数据库的索引机制。

哈希表的实现需要解决哈希冲突的问题，即两个不同的键可能会映射到同一个哈希值。常见的冲突解决方法有链地址法和开放地址法。链地址法通过在每个哈希桶中链接所有冲突的元素形成链表，而开放地址法通过顺序探查或者二次探查来找到下一个空闲的哈希桶。

下面是一个简单的哈希表实现示例，使用链地址法解决哈希冲突：

class HashTable:
    def __init__(self, size):
        self.size = size
        self.table = [[] for _ in range(size)]

    def hash_function(self, key):
        return hash(key) % self.size

    def insert(self, key, value):
        hash_key = self.hash_function(key)
        key_exists = False
        bucket = self.table[hash_key]
        for i, kv in enumerate(bucket):
            k, _ = kv
            if key == k:
                key_exists = True
                break
        if key_exists:
            bucket[i] = ((key, value))
        else:
            bucket.append((key, value))

    def search(self, key):
        hash_key = self.hash_function(key)
        bucket = self.table[hash_key]
        for k, v in bucket:
            if key == k:
                return v
        return None

    def remove(self, key):
        hash_key = self.hash_function(key)
        bucket = self.table[hash_key]
        key_exists = False
        i = 0
        for k, v in bucket:
            if key == k:
                key_exists = True
                break
            i += 1
        if key_exists:
            del bucket[i]

在上述代码中，`HashTable` 类包含一个哈希表，它初始化时会根据指定大小创建一个二维数组作为存储结构。`hash_function` 方法用于计算键的哈希值并进行模运算以获得索引。`insert` 方法用于插入新的键值对，如果键已存在，则更新其值。`search` 方法用于根据键查找对应的值。`remove` 方法用于根据键删除键值对。

哈希表的关键在于哈希函数的设计。一个理想的哈希函数应该尽量减少哈希冲突，均匀分散数据到各个哈希