深入浅出Python图形算法：从树形结构到图论的探索

# 1. 图形算法的基础概念与重要性

图形算法是解决复杂数据关系和网络结构问题的关键技术。在信息技术飞速发展的今天，图形算法的地位愈发重要。它们不仅在计算机科学中占据核心地位，还广泛应用于网络分析、社交网络、路径规划以及生物信息学等领域。

## 1.1 基础概念

图形算法的基础是图论，其核心是图（Graph），一种抽象的数据结构，表示为 G = (V, E)，其中 V 代表顶点（Vertices）集合，E 代表边（Edges）集合。理解图的表示和操作对于掌握图形算法至关重要。

## 1.2 重要性

图形算法的重要性体现在其解决实际问题的能力上。例如，在社交网络分析中，通过图形算法可以识别社群结构、影响力传播路径等；在物流领域，路径规划和最短路径问题直接关系到运营效率和成本控制。

## 1.3 应用场景

除了上述场景，图形算法还广泛应用于网络通信、推荐系统、电子电路设计等众多领域。掌握图形算法不仅能够解决专业领域问题，还能提高数据分析和处理的效率，对于IT行业从业者而言，这是一个极具价值的技能提升方向。

# 2. 树形结构详解及其应用

### 2.1 树形结构的基本理论

树形结构是数据结构中非常重要的一部分，尤其是二叉树。在计算机科学中，树是由一个集合和一个在该集合上定义的偏序关系组成的一个无环图。

#### 2.1.1 树和二叉树的定义

树是n个节点的有限集合，n≥0。若n=0，则空树，无节点；若n>0，则满足以下条件：
1. 有一个特定的节点称为根节点(root)；
2. 其余节点可以分为m（m>0）个互不相交的有限集，每一个集合本身又是一棵树，称为根节点的子树。

二叉树是每个节点最多有两个子树的树结构，通常子树被称作“左子树”和“右子树”。二叉树有五种基本形态：空树、只有一个根节点、只有左子树、只有右子树和既有左子树又有右子树。

#### 2.1.2 树的遍历算法

树的遍历算法包括前序遍历（Pre-order）、中序遍历（In-order）和后序遍历（Post-order）。另外，对于二叉树还有一个层次遍历（Level-order）算法。

前序遍历是先访问根节点，然后遍历左子树，最后遍历右子树；中序遍历则是先遍历左子树，再访问根节点，最后遍历右子树；后序遍历先遍历左子树，接着遍历右子树，最后访问根节点。层次遍历则按照树的层级从上往下、从左到右依次访问每一个节点。

### 2.2 树形结构在算法中的应用

树形结构在计算机算法中有着广泛的应用，它不仅简单直观，而且效率高，易于实现。

#### 2.2.1 堆排序和优先队列

堆是一种特殊的完全二叉树，每个节点的值都大于或等于其子节点的值，这样的堆被称为大顶堆。堆的这种特性非常适合实现优先队列。

堆排序算法是一种基于比较的排序算法，利用堆这种数据结构所设计的一种排序算法。它的基本思想是将待排序的序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点，将它移走后，再对剩余的n-1个元素重新构建大顶堆，使得每次取出堆顶元素都是剩余元素的最大值，如此反复执行，从而得到一个有序序列。

#### 2.2.2 哈夫曼编码和数据压缩

哈夫曼编码是一种广泛应用于数据压缩的编码方法。它基于字符出现的频率来构建最优的前缀编码，频率高的字符使用较短的编码，频率低的字符使用较长的编码。

哈夫曼树是构造哈夫曼编码的基础。构建哈夫曼树的过程中，字符被视为带权路径长度的叶子节点，通过不断地合并权值最小的两个节点生成新的内部节点，直至树中只剩一个节点。这个节点的路径长度代表了该字符的编码长度。

### 2.3 树的优化与扩展

树的优化和扩展往往是为了保持树的平衡或者提高查找、插入和删除操作的效率。

#### 2.3.1 平衡二叉树（AVL树）

AVL树是一种自平衡的二叉搜索树，对于任何一个节点，其左右子树的高度差不能超过1。AVL树的这种特性保证了树的平衡，从而确保了插入、删除、查找等操作的时间复杂度为O(log n)。

#### 2.3.2 红黑树及其性质

红黑树是一种具有自平衡功能的二叉搜索树。它通过五个性质来维持平衡：
1. 每个节点要么是红色，要么是黑色；
2. 根节点是黑色；
3. 每个叶子节点（NIL节点，空节点）是黑色；
4. 如果一个节点是红色的，则它的两个子节点都是黑色的；
5. 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点。

红黑树的这些性质确保了最长路径不会超过最短路径的两倍，因此最坏情况下插入、删除、查找操作的效率也为O(log n)。

在本章节中，我们深入了解了树形结构的基础理论，及其在算法中的各种应用。下一章节，我们将探索图论的基础知识，以及图的表示方法和应用。

# 3. 图论基础与图的表示方法

## 3.1 图论的核心概念

### 3.1.1 图的定义与分类

图论是数学的一个分支，研究的是由对象和这些对象之间的关系所构成的网络结构。在计算机科学中，图广泛用于表示数据之间的关系，如社交网络、网页链接、电路设计等。

图由一组顶点（也称为节点）和连接这些顶点的边组成。图可以是有向的（边具有方向）或无向的（边没有方向）。有向图中，边从一个顶点指向另一个顶点，表示方向性关系；无向图中，边连接两个顶点，表示无方向性关系。

#### 表格：图的分类

| 图类型 | 描述 | 应用场景 |
| --- | --- | --- |
| 无向图 | 边没有方向，表示两个顶点之间有连接 | 社交网络、电路图 |
| 有向图 | 边有方向，表示从一个顶点到另一个顶点的流向 | 网页链接、任务调度 |
| 加权图 | 边具有权重，用于表示成本、距离等 | 最短路径问题、网络设计 |
| 非加权图 | 边不具有权重 | 拓扑排序、图连通性检测 |

### 3.1.2 图的遍历算法（深度优先与广度优先）

图的遍历是图论中一个重要的操作，目的是访问图中的每个顶点恰好一次。遍历算法主要有深度优先搜索（DFS）和广度优先搜索（BFS）两种。

#### 深度优先搜索（DFS）

深度优先搜索遵循的原则是尽可能深地搜索图的分支。当节点v的所有边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这个过程一直进行到已发现从源节点可达的所有节点为止。

**DFS的伪代码：**

DFS(v)
  if v is already visited
    return
  mark v as visited
  for each unvisited neighbor u of v
    DFS(u)

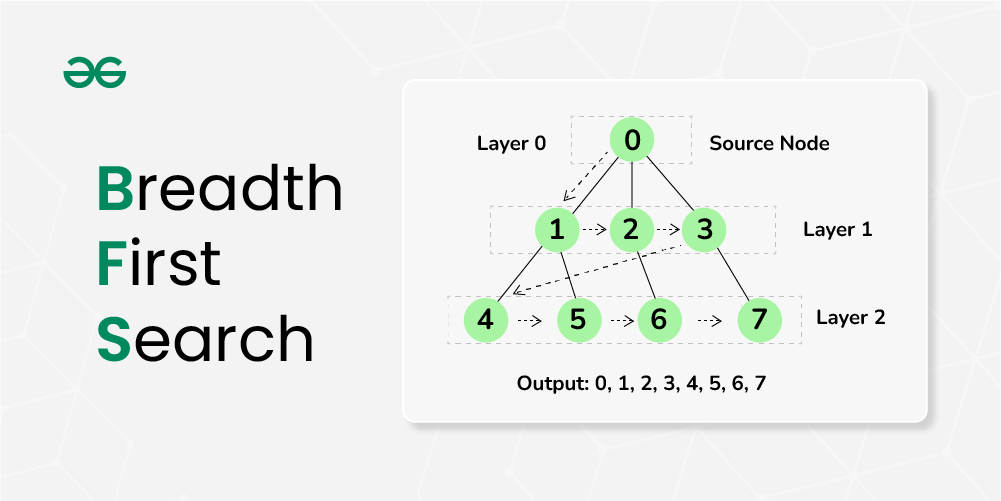
#### 广度优先搜索（BFS）

广度优先搜索从一个节点开始，访问所有邻近的节点，然后再对每个邻近节点进行相同的操作。BFS使用队列数据结构来追踪待访问的节点。

**BFS的伪代码：**

BFS(v)
  create queue Q
  enqueue v to Q
  mark v as visited
  while Q is not empty
    t = Q.front()
    Q.pop()
    for each unvisited neighbor u of t
      mark u as visited
      enqueue u to Q

## 3.2 图的存储结构

### 3.2.1 邻接矩阵与邻接表

图的存储结构决定了图如何在计算机内存中表示，通常有两种主要方法：邻接矩阵和邻接表。

#### 邻接矩阵

邻接矩阵是表示图的一种方式，矩阵的每个元素表示一对顶点之间是否存在边。对于无向图来说，邻接矩阵是对称的；对于有向图，邻接矩阵可能不对称。

**邻接矩阵的特点：**

- 对于无向图：矩阵是对称的，如果顶点i和顶点j之间存在一条边，则matrix[i][j]和matrix[j][i]都为1。
- 对于有向图：如果存在从顶点i到顶点j的一条边，则matrix[i][j]为1。

#### 邻接表

邻接表是另一种表示图的方法，它使用链表来表示图中的所有邻接顶点。每个顶点有一个链表，链表中的元素表示所有与该顶点相邻的顶点。

**邻接表的特点：**

- 对于无向图：每个顶点的链表包含所有与该顶点相邻的顶点。
- 对于有向图：每个顶点的链表包含所有从该顶点出发的边所连接的顶点。

#### 表格：邻接矩阵与邻接表的比较

| 特征 | 邻接矩阵 | 邻接表 |
| --- | --- | --- |
| 空间复杂度 | O(V^2) | O(V + E) |
| 实现复杂度 | 简单 | 较复杂 |
| 邻接点访问速度 | 较慢 | 较快 |
| 存储是否对称 | 有向图不对称，无向图对称 | 都可以 |
| 稀疏图表现 | 浪费空间 | 更高效 |

### 3.2.2 边集数组表示法

边集数组（也称为边列表）是另一种图的表示方法，它使用一个数组来存储图中所有的边。每条边用一对顶点来表示。

**边集数组的特点：**

- 对于无向图和有向图，每条边可以表示为一个包含两个顶点的数组。
- 适合表示稀疏图，因为它只存储边信息，而不是整个矩阵。
- 边集数组通常也包含权重信息（如果图是加权图）。

## 3.3 图算法的实战应用

### 3.3.1 最短路径问题（Dijkstra和Floyd算法）

图论中的最短路径问题指的是在一个带权图中找到两个顶点之间的最短路径。Dijkstra算法用于单源最短路径问题，而Floyd算法用于所有顶点对之间的最短路径问题。

#### Dijkstra算法

Dijkstra算法是一种单源最短路径算法，用于在加权图中找到一个顶点到其他所有顶点的最短路径。算法的核心思想是贪心策略。

**Dijkstra算法的步骤：**

1. 创建两个集合：S和U，S集合包含已经找到最短路径的顶点，U集合包含其他顶点。
2. 初始化最短路径估计值，对于起点v，它到自身的距离为0，到其他所有顶点的距离为无穷大。
3. 当集合U非空时，执行以下操作：
a. 从未处理过的顶点中找到距离集合S最近的顶点u。
b. 将顶点u添加到集合S中。
c. 更新顶点u的所有邻接顶点的最短路径估计值。

def dijkstra(graph, source):
    # 初始化距离表，所有顶点到源点的距离设为无穷大
    dist = {vertex: float('infinity') for vertex in graph}
    # 源点到自己的距离是0
    dist[source] = 0
    # 最短路径树集合
    path = {vertex: None for vertex in graph}
    while dist:
        # 寻找未处理的最小距离顶点
        min_vertex = min(dist, key=dist.get)
        path_to_min_vertex = path[min_vertex]
        # 如果该顶点距离无穷大，则表示图中不存在该顶点到源点的路径
        if dist[min_vertex] == float('infinity'):
            break
        # 将当前顶点从未处理顶点集合中移除，添加到已处理顶点集合
        del dist[min_vertex]
        # 遍历当前顶点的所有邻接顶点
        for neighbor, weight in graph[min_vertex].items():
            if neighbor not in dist:
                continue
            # 更新邻接顶点的距离值和路径
            if dist[min_vertex] + weight < dist[neighbor]:
                dist[neighbor] = dist[min_vertex] + weight
                path[neighbor] = min_vertex
    return dist, path

#### Floyd算法

Fl