Epochs与模型复杂度

# 1. 机器学习中的Epochs概念

在机器学习中，Epochs（或称为"周期"或"轮次"）是指整个训练数据集通过神经网络一次的完整过程。Epochs的数量对模型的训练效果和性能有着直接的影响。理解Epochs的原理是优化训练过程和避免过拟合或欠拟合的关键。

## 1.1 Epochs的基本概念

一个Epochs意味着数据集中的所有样本都已被用于训练一次。在多个Epochs中，每个样本可能被多次用作训练，以帮助网络调整其权重和偏差。随着Epochs数目的增加，模型理论上会越来越接近最优解，但同时也可能逐渐过度拟合训练数据。

## 1.2 Epochs的选择与训练策略

选择合适数量的Epochs是一个关键的决策。太少，模型可能未充分学习；太多，则可能导致过拟合。通常，通过在验证集上的性能监控来决定何时停止训练，这种方法被称为Early Stopping。在实践中，可以使用交叉验证或模型验证曲线来辅助决策。

## 1.3 Epochs与模型泛化能力的关系

Epochs数不仅影响模型在训练集上的表现，也影响其在未见数据上的泛化能力。一个平衡点是在训练数据上表现良好而不过度拟合的状态。适当的Epochs数有助于找到这一平衡点，从而提高模型的整体性能。

// 示例：使用PyTorch设置Epochs
import torch
from torch import nn
from torch.optim import Adam

model = nn.Sequential(...) # 创建模型
loss_function = nn.CrossEntropyLoss()
optimizer = Adam(model.parameters(), lr=0.001)

epochs = 100 # 设置Epochs数量
for epoch in range(epochs):
    # 训练模型...
    # 验证模型...

在接下来的章节中，我们将深入探讨模型复杂度的理论基础，以及它如何与Epochs、过拟合、欠拟合和学习率等因素相互作用。

# 2. 模型复杂度的理论基础

### 2.1 模型复杂度的定义与重要性

#### 2.1.1 模型复杂度的定义

在机器学习和深度学习领域中，模型复杂度是描述模型能够捕捉数据多样性的能力的一个概念。具体来说，它可以被理解为模型对数据进行拟合时的灵活性或者说是模型对问题的复杂性的表示能力。一个复杂度高的模型能够学习到训练数据中更复杂的模式，而复杂度低的模型则只能捕捉到简单的模式。模型复杂度可以是显式地由模型结构决定的，比如网络层数和神经元数量，也可以是隐式地由模型学习的参数决定的。

在数学上，模型复杂度可以用几种不同的方式来量化。其中一种常见的度量是VC维（Vapnik–Chervonenkis dimension），它衡量的是模型可以分类的训练数据点的最大数目。但是，VC维是一个理论概念，在实际应用中并不总是容易计算。

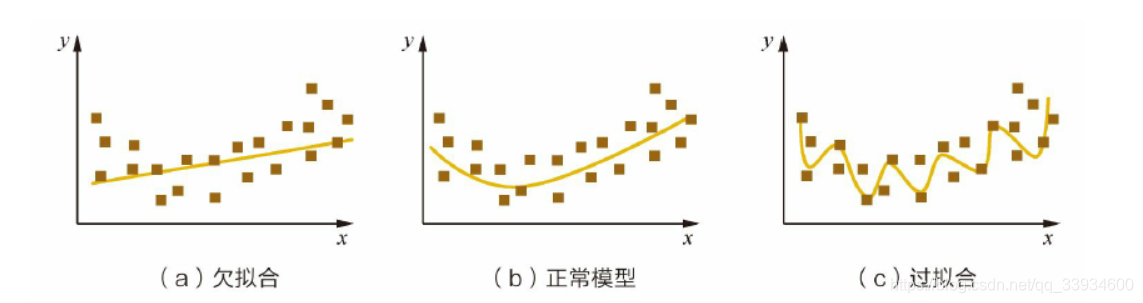
#### 2.1.2 模型复杂度与过拟合、欠拟合的关系

过拟合和欠拟合是模型训练过程中常见的两个问题，它们与模型复杂度息息相关。过拟合发生在模型对训练数据学习得太好，以至于捕捉到了数据中的噪声而非底层的真实分布，这通常是由模型过于复杂导致的。相反，欠拟合则是指模型太简单，无法捕捉到数据中的模式，这通常发生在模型复杂度不足时。

要找到二者之间的平衡，需要对模型复杂度进行适当的控制。例如，在过拟合的情况下，降低模型复杂度，或者使用正则化技术来防止模型过分依赖于训练数据。在欠拟合的情况下，可以尝试增加模型复杂度，如增加更多的层或参数，或者引入更多的特征。

### 2.2 模型复杂度的度量方法

#### 2.2.1 维度的概念及其影响

在机器学习中，维度通常指输入数据的特征数量。但是，维度的概念也可以推广到模型复杂度的度量中。在参数模型中，比如线性回归模型，维度直接对应于参数的数量。而在非参数模型中，维度可以被理解为模型的容量，也就是模型能够捕获数据复杂性的能力。

维度的增加通常意味着模型复杂度的提升。高维数据提供了更多的信息，但也引入了更高的计算成本和更大的过拟合风险。处理高维数据，尤其是在小样本情况下，需要使用诸如主成分分析（PCA）等降维技术来减少特征空间的维度，从而控制模型复杂度。

#### 2.2.2 参数数量与模型容量

参数数量是衡量模型复杂度的另一个直观方法。一个模型的参数包括权重、偏置以及其它可能的训练变量。参数的增加通常会导致模型能够表示更复杂的数据关系，但也可能造成过拟合。

在神经网络中，参数数量通常与网络的宽度和深度相关。网络宽度指的是单个层中的节点数，而网络深度指的是层数的总数。增加宽度或深度都会增加模型的参数数量，从而增加模型复杂度。模型选择过程中，必须平衡参数数量和模型性能之间的关系，防止过拟合同时确保模型有足够的表达能力。

#### 2.2.3 正则化项在衡量复杂度中的应用

正则化是在模型训练过程中防止过拟合的一种常用技术。在正则化方法中，比如L1（Lasso）或L2（Ridge）回归，会在损失函数中加入一个额外的项，该项与模型参数的某些函数相关，如参数的平方或绝对值。正则化项的加入，限制了参数的大小，从而间接限制了模型的复杂度。

L1正则化可以导致模型参数的稀疏，也就是某些参数会变为零，这可以看作是一种模型选择机制，通过移除一些不重要的特征来降低模型复杂度。L2正则化则倾向于平滑模型参数，防止参数中的极端值，从而减少过拟合的风险。在实际应用中，选择合适的正则化项和强度，是调整模型复杂度和防止过拟合的重要手段。

### 2.3 模型复杂度与学习率的关系

#### 2.3.1 学习率对模型训练的影响

学习率是训练深度学习模型时一个重要的超参数，它决定了模型权重更新的快慢。如果学习率设置得过高，模型可能会在损失函数的最优点附近震荡，甚至发散；而如果学习率设置得过低，模型训练将会非常缓慢，甚至陷入局部最优点。

在复杂度较高的模型中，正确设置学习率尤为重要，因为复杂模型有更多的参数，更容易发生训练中的震荡和发散。学习率的调整通常需要通过实验来进行，但近年来，自适应学习率优化算法，如Adam、RMSprop等，已经被开发出来，可以在一定程度上自动化地选择合适的学习率。

#### 2.3.2 调整学习率以控制模型复杂度

调整学习率不仅影响模型的训练效率，还与模型的最终性能密切相关。在面对复杂模型时，选择适当的学习率对于防止过拟合和欠拟合都至关重要。一个较低的学习率可以帮助模型更好地收敛到最小损失，但可能会导致模型无法学到足够复杂的数据模式。

为了在保证学习效率的同时防止过拟合，可以通过学习率衰减策略来实现。比如，在训练过程中逐步减小学习率，可以让模型在训练初期快速收敛，而在后期进行更细致的调整。此外，还可以使用学习率预热技术，即在训练初期逐渐增加学习率，使得模型能够快速跳出局部最小值。

通过调整学习率来控制模型复杂度，需要模型开发者对数据集和模型有较深入的理解，同时还需要通过实验来确定最佳的学习率策略。在实际操作中，可能会结合使用多种学习率调整策略，以期达到最佳的训练效果。

# 3. Epochs与模型训练

## 3.1 Epochs对模型学习过程的作用

### 3.1.1 Epochs的定义与影响

Epochs表示整个训练集数据被模型完整地学习一次的次数。在神经网络训练中，一个Epoch意味着所有的训练样本都已经被用来更新网络权重。学习率、数据集大小以及批处理大小都会影响Epochs的选择。若Epochs过小，则模型可能无法从数据中学到足够的信息；相反，过高的Epochs则可能导致模型过拟合，失去泛化能力。

### 3.1.2 Epochs与训练集、验证集的关系

在训练过程中，通常将数据集分为训练集和验证集。训练集用于更新模型权重，而验证集用于监控模型性能，保证模型不过度拟合训练数据。Epochs的增加会影响模型在训练集和验证集上的性能表现。随着Epochs的增加，模型在训练集上的准确度往往会逐渐提高，但到达一定阈值后，验证集上的准确度可能会开始下降，这表明模型开始过拟合。

## 3.2 如何选择合适的Epochs数目

### 3.2.1 Early Stopping技术

为了防止模型过拟合，一种常用的技术是Early Stopping。这是一种监控验证集性能，并在性能不再提升时停止训练的策略。早期停止通常会设定一个容忍度（patience），例如，在连续几个Epochs中，验证集的性能没有显著提升时停止训练。

### 3.2.2 基于验证集性能的Epochs确定方法

选择合适的Epochs数目还可以基于对验证集性能的观察。一种方法是绘制训练曲线，即在每个Epoch后记录训练集和验证集的准确度或损失值，并绘制出曲线图。理想的Epoch数目应该是在验证集性能开始下降之前停止训练的点。这通常通过观察曲线的“转折点”来确定，即验证集性能达到最高点，之后开始平坦或下降的点。

## 3.3 Epochs对模型性能的长期影响

### 3.3.1 Epochs数与模型泛化能力的平衡

Epochs的选择需要平衡模型的训练集性能与泛化能力。一个较低的Epoch数可能会导致模型未能充分学习训练数据的特征，而较高的Epoch数可能会导致模型学习到