【神经网络优化技术深度分析】：从理论到实践

# 1. 神经网络优化技术概述

神经网络优化技术作为机器学习和深度学习领域的核心，旨在提高模型的泛化能力、减少训练时间，并提升计算效率。随着深度学习应用的不断扩展，优化技术也日趋成熟，从基础的梯度下降算法到自适应学习率算法，再到更高级的技术如牛顿法和拟牛顿法，都有助于解决不同层次的问题。掌握这些技术，不仅能够提升模型性能，还能够推动人工智能在医疗、金融、自动驾驶等行业的创新应用。在本章中，我们将对优化技术的发展历程、重要性以及它在各个领域的应用进行概述，为接下来章节的深入探讨打下基础。

# 2. 神经网络基础理论

## 2.1 神经网络的数学模型

### 2.1.1 激活函数的种类与特性

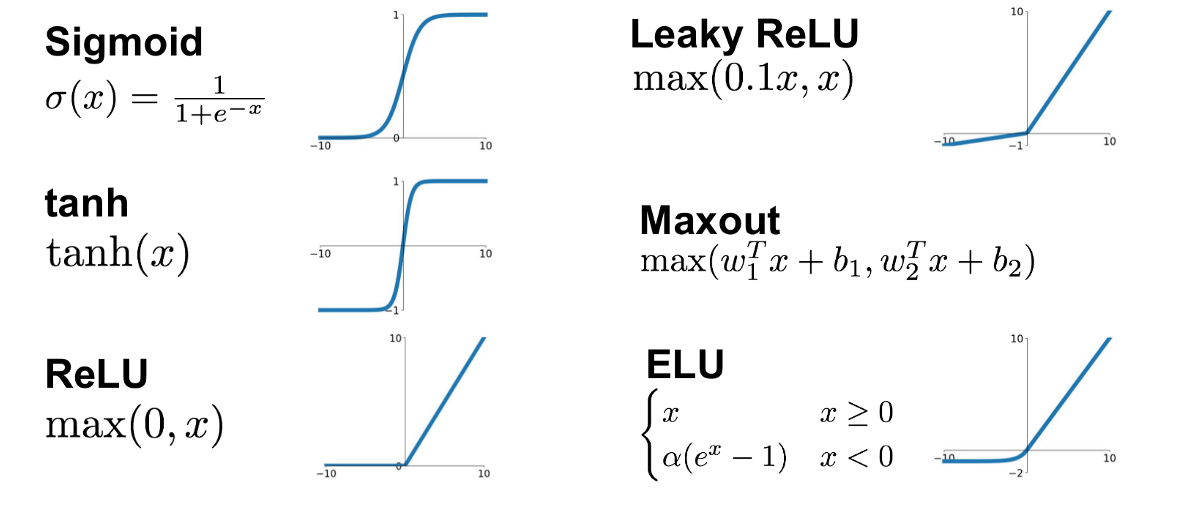
激活函数是神经网络中最重要的组成部分之一，它为网络引入了非线性因素，使得神经网络能够解决更复杂的问题。以下是几种常见的激活函数及其特性：

1. Sigmoid 函数：它的数学表达式为 \( \sigma(x) = \frac{1}{1+e^{-x}} \)，输出范围为 (0, 1)。Sigmoid 函数的主要特性是它能够将输入压缩至 (0, 1) 区间内，模拟了生物神经元中的“激发”和“抑制”状态。然而，它也存在一些问题，比如梯度消失和输出不是零中心化，这可能导致收敛速度变慢。

2. Tanh 函数：Tanh 函数数学表达式为 \( \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \)，输出范围为 (-1, 1)。Tanh 函数与 Sigmoid 函数类似，但是输出是零中心化的，有助于缓解梯度消失问题。

3. ReLU 函数：ReLU 函数的数学表达式为 \( f(x) = \max(0, x) \)，当 \( x < 0 \) 时，函数值为 0；当 \( x \geq 0 \) 时，函数值为 \( x \)。ReLU 函数是目前使用最广泛的激活函数，因为它的计算速度快，且在一定程度上缓解了梯度消失问题。但是，ReLU 存在一个问题，即“ReLU 死亡”，部分神经元可能永远不会被激活。

4. Leaky ReLU 和 Parametric ReLU：为了解决 ReLU 死亡问题，出现了 Leaky ReLU 和 Parametric ReLU，它们允许负值通过一个很小的斜率，从而避免了某些神经元的死亡。

5. ELU 函数：ELU 函数的数学表达式为 \( f(x) = \begin{cases}
x & \text{if } x \geq 0 \\
\alpha (e^x - 1) & \text{if } x < 0
\end{cases} \)，其中 \( \alpha \) 是一个超参数。ELU 函数结合了 ReLU 和 Leaky ReLU 的优点，引入了指数项来加速学习过程。

### 2.1.2 权重初始化方法

权重初始化方法对神经网络的收敛性有着直接的影响。以下是一些常用的权重初始化方法：

1. 零初始化：所有权重初始化为 0。这种初始化方法会导致所有神经元在前向传播时输出相同的值，反向传播时，权重的更新也会相同，这称为对称权重问题，不利于模型的学习。

2. 随机初始化：权重从一个较小的随机值分布（如正态分布或均匀分布）中采样。这种初始化方法打破了对称权重问题，使得网络可以开始学习不同的特征。

3. 基于方差的初始化：如Xavier初始化（也称为Glorot初始化），它的核心思想是使每层的方差保持一致。权重从一个特定的分布中采样，分布的方差与上一层的单元数成比例。

4. He初始化：是一种变体，特别适用于ReLU激活函数，权重是从一个以 \( \sqrt{2/n} \) 为标准差的正态分布中采样，其中 \( n \) 是当前层神经元的数量。

### 2.1.3 梯度消失与爆炸问题

在神经网络的训练过程中，梯度消失和爆炸是两个需要特别注意的问题：

- 梯度消失：指的是随着反向传播进行，梯度越来越小，导致底层的权重更新非常缓慢或几乎不更新。这通常发生在使用 Sigmoid 或 Tanh 这类激活函数时，因为它们的导数在输入值大或小的情况下接近于零。

- 梯度爆炸：与梯度消失相反，梯度爆炸意味着梯度非常大，导致权重更新过大，甚至破坏已经学习到的权重值。

解决这些问题的方法包括使用 ReLU 或者其变体作为激活函数、适当正则化、使用批量归一化（Batch Normalization）以及梯度剪切等技术。

## 2.2 反向传播算法

### 2.2.1 梯度下降与变种

梯度下降是一种优化算法，用于训练神经网络和其他机器学习模型。它的核心思想是根据损失函数相对于模型参数的梯度来更新参数，从而减少损失函数的值。

1. 基本梯度下降：参数 \( \theta \) 的更新公式为 \( \theta = \theta - \eta \nabla_\theta J(\theta) \)，其中 \( \eta \) 是学习率，\( \nabla_\theta J(\theta) \) 是损失函数 \( J(\theta) \) 相对于参数的梯度。基本梯度下降是一种批量梯度下降，需要遍历整个数据集才能进行一次更新。

2. 随机梯度下降（SGD）：与批量梯度下降不同，SGD 在每次迭代中只使用一个样本数据进行参数更新，这使得更新更频繁，但也带来了较大的噪声。

3. 小批量梯度下降（Mini-batch Gradient Descent）：介于批量梯度下降和随机梯度下降之间，每次迭代使用一小批量数据进行参数更新，这种方法是目前最常用的。

4. 变种如带动量的梯度下降（Momentum）、自适应学习率算法（如 Adam 和 RMSprop）等，将在后续章节中详细介绍。

### 2.2.2 链式法则在反向传播中的应用

链式法则是微积分中的一个重要规则，用于计算复合函数的导数。在神经网络中，链式法则用于从输出层向输入层反向传播误差，从而更新网络参数。

设 \( y \) 是输出，\( x \) 是输入，中间有 \( n \) 层网络，链式法则可以递归地应用于计算 \( \frac{\partial y}{\partial x} \)，即 \( y \) 相对于 \( x \) 的导数。这个过程可以用下式表示：

\[
\frac{\partial y}{\partial x} = \frac{\partial y}{\partial h_n} \cdot \frac{\partial h_n}{\partial h_{n-1}} \cdot \ldots \cdot \frac{\partial h_2}{\partial h_1} \cdot \frac{\partial h_1}{\partial x}
\]

在实际编程中，我们用反向传播算法来实现链式法则。在神经网络框架中，如TensorFlow或PyTorch，这个过程被自动实现，我们只需要定义网络结构和损失函数即可。

### 2.2.3 反向传播算法流程

反向传播算法的大致流程如下：

1. 前向传播：输入数据通过网络，每一层计算其输出，直到最终的预测值。

2. 计算损失：使用损失函数 \( J(\theta) \) 计算预测值和实际值之间的差异，即损失值。

3. 反向传播误差：从输出层开始，根据链式法则计算每一层的误差导数，直到第一层。

4. 更新参数：根据计算出的梯度和学习率更新每一层的权重和偏置。

5. 重复步骤1-4，直到网络收敛或达到预设的迭代次数。

接下来将探讨神经网络训练中的技巧，比如处理过拟合与欠拟合以及批归一化和丢弃法等内容。

## 2.3 神经网络的训练技巧

### 2.3.1 过拟合与欠拟合的处理

在训练神经网络时，我们希望模型能够很好地泛化到未知数据上。然而，模型可能会出现两种问题：过拟合和欠拟合。

1. 过拟合（Overfitting）：模型在训练数据上表现很好，但是在验证集或测试集上表现差。这通常是因为模型过于复杂，学习了训练数据中的噪声和特定细节。

2. 欠拟合（Underfitting）：模型在训练数据上表现不佳，也没有泛化到新数据的能力。这通常是因为模型太简单，不能捕捉数据中的本质特征。

为了缓解过拟合，可以采取以下措施：

- 数据增强：通过对训练数据应用一系列转换（如旋转、缩放、裁剪等），人为增加训练数据的多样性和数量。

- 早停（Early Stopping）：在验证集上的性能不再提升时停止训练，防止模型继续过拟