【激活函数比较】：选择合适的激活函数，激活神经网络潜力

# 1. 激活函数在神经网络中的作用

神经网络作为深度学习的核心，其性能的优劣在很大程度上取决于网络结构的配置。在这些配置中，激活函数的选择尤为关键。激活函数负责引入非线性因素，这对于网络的表达能力至关重要。简单来说，激活函数可以决定网络能否解决复杂的问题，如图像识别、自然语言处理等。它在神经元输出中增加非线性变换，使得深度网络能够学习和模拟复杂的函数映射关系。

## 2.1 理解激活函数的基本概念

### 2.1.1 激活函数的定义和重要性

激活函数是一个数学函数，它将神经元的输入或神经元的加权总和（净输入）转换成输出。通常，这个输出被用来作为下一层神经元的输入。在没有激活函数的情况下，不管网络有多少层，最终都只是线性映射。因此，激活函数是赋予网络非线性性质的关键。

### 2.1.2 激活函数在神经网络中的角色

在神经网络中，激活函数的选择对网络能否学习复杂的模式有很大影响。它不仅帮助网络学习和模拟非线性函数，而且还有助于在反向传播算法中计算梯度，从而允许权重的更新。没有激活函数的网络将无法解决非线性问题，因此激活函数是构建有效神经网络模型不可或缺的部分。

通过这些基础概念的理解，我们可以开始深入探讨具体激活函数的特性及其在实际神经网络中的应用。接下来的章节中，我们将详细介绍和分析多种基础激活函数的特性和局限性。

# 2. 基础激活函数概述

## 2.1 理解激活函数的基本概念

### 2.1.1 激活函数的定义和重要性

激活函数是神经网络中非常关键的组成部分，它们的作用是引入非线性因素，使得神经网络能够解决非线性问题。如果没有激活函数，无论神经网络有多少层，最终都只能表示线性映射。激活函数对输入信号进行处理，并决定是否以及如何向神经网络的下一层传递该信号。

### 2.1.2 激活函数在神经网络中的角色

在神经网络中，激活函数对输出进行非线性转换，这样的转换使得网络能够学习和执行更复杂的功能。激活函数位于神经元的输出端，它的值通常被用作下一层输入信号的一部分，帮助网络捕捉输入数据中的复杂模式。

## 2.2 常见基础激活函数详解

### 2.2.1 Sigmoid函数：历史与局限性

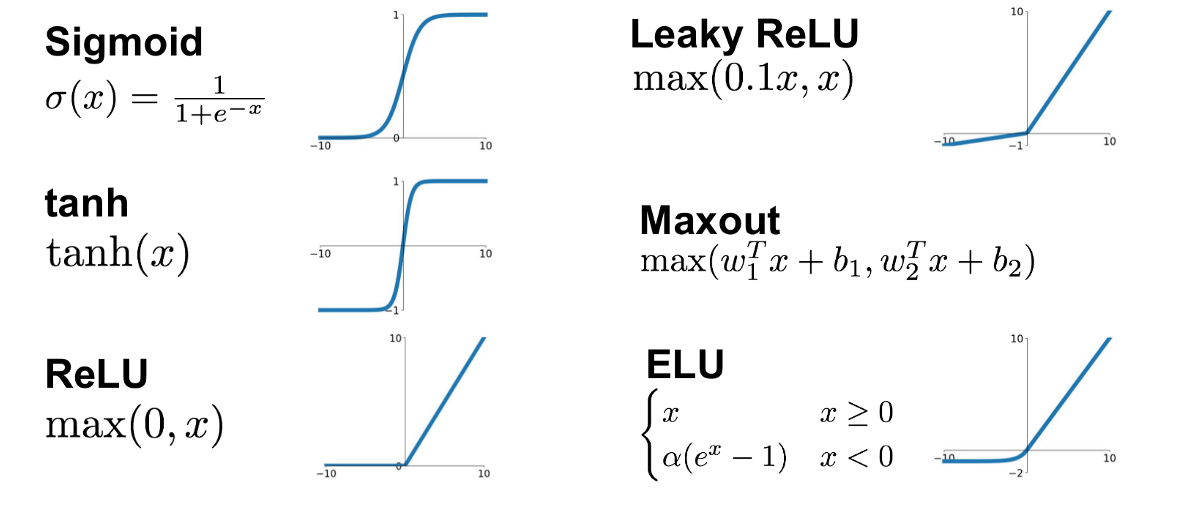
Sigmoid函数是最古老也是最著名的激活函数之一，其数学表达式为 σ(x) = 1 / (1 + e^(-x))。Sigmoid函数将任意实数值压缩至(0, 1)区间内，非常适合于二分类问题。然而，Sigmoid函数也存在一些局限性，包括饱和性问题和梯度消失问题。

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.linspace(-10, 10, 100)
y = sigmoid(x)

import matplotlib.pyplot as plt
plt.plot(x, y)
plt.title('Sigmoid Function')
plt.xlabel('Input value (x)')
plt.ylabel('Activation output')
plt.grid()
plt.show()

### 2.2.2 Tanh函数：与Sigmoid的比较

Tanh函数是Sigmoid函数的变形，数学表达式为 tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))。与Sigmoid函数相比，Tanh函数的输出范围是(-1, 1)，它能够帮助神经网络将输入数据映射到更宽的范围，但同样存在梯度消失的问题。

### 2.2.3 ReLU函数：现代神经网络的选择

ReLU（Rectified Linear Unit）函数是一个更加现代的选择，其表达式为 f(x) = max(0, x)。ReLU能够缓解梯度消失问题，并且计算效率较高，因此在现代神经网络架构中非常流行。然而，ReLU也有缺点，如死亡ReLU问题，其中神经元可能永久不激活。

以上，我们对激活函数的定义、重要性、以及常见的基础激活函数Sigmoid、Tanh和ReLU进行了概述和分析。在接下来的章节中，我们将进一步探讨高级激活函数的引入背景、原理以及它们在理论和实践中的应用。

# 3. 高级激活函数探索

## 3.1 高级激活函数的引入背景

### 3.1.1 解决基础激活函数的缺点

随着神经网络的发展，基础激活函数在特定情况下暴露出诸多问题。例如，Sigmoid和Tanh函数在处理大数据时，容易导致梯度消失，这在深层网络中尤其突出。这些问题严重阻碍了神经网络在更深层次和更复杂任务中的应用。因此，为了突破这些限制，研究人员开始设计能够更好地适应现代神经网络需求的高级激活函数。

### 3.1.2 推动神经网络性能的提升

高级激活函数不仅仅弥补了基础激活函数的不足，还直接推动了神经网络性能的提升。在诸如图像识别、自然语言处理等领域，高级激活函数通过减少饱和区和维持更积极的梯度，使得网络能够更快地收敛，并在一定程度上提升了模型的泛化能力。

## 3.2 主要高级激活函数解析

### 3.2.1 Leaky ReLU与它的变种

Leaky ReLU是ReLU的一种变体，它解决了ReLU在负区间输出为零的问题。Leaky ReLU通过引入一个很小的斜率α，允许在输入小于零时有一些小的非零梯度流过。其数学表达式为：

f(x) = 
\begin{cases} 
  x & \text{if } x > 0 \\
  \alpha x & \text{if } x \leq 0
\end{cases}

其中，`α` 是一个小于1的常数。这样的改进使得网络即使在负输入时也不会完全死掉，从而减轻了ReLU的死亡ReLU问题。

### 3.2.2 ELU和PReLU：负值处理的改进

Exponential Linear Unit (ELU)和Parametric Rectified Linear Unit (PReLU)进一步对负值处理进行了改进。ELU通过引入指数函数来保证输出的平均值接近零，PReLU则类似于Leaky ReLU，但`α`是一个可以学习的参数。

ELU的表达式为：

f(x) = 
\begin{cases} 
  x & \text{if } x > 0 \\
  \alpha (e^x - 1) & \text{if } x \leq 0
\end{cases}

ELU在负区间提供了平滑的曲线，有助于缓解梯度消失的问题，并且输出的平均值接近零，有助于加快学习速度。

### 3.2.3 Swish与GELU：性能与效率的新选择

Swish和Gaussian Error Linear Unit (GELU)是近年来出现的更为先进的激活函数。Swish由Google研究人员提出，其自身就是通过神经网络学习得到的。Swish的公式为：

f(x) = x \cdot \sigma(\beta x) = \frac{x}