【递归边界问题解决】：Python递归限制突破与优化策略

# 1. 递归算法基础与边界问题

递归算法是计算机科学中一种重要的编程技术，其思想是函数直接或间接调用自身来解决问题。递归在解决分治问题、树和图遍历等场景中表现尤为突出。但递归也存在边界问题，尤其是递归深度的限制，这通常是由系统栈空间有限引起的。

理解递归的基础，关键是要掌握递归函数的设计与终止条件的设定。一个典型的递归函数通常包含两个主要部分：基本情况（base case）和递归步骤（recursive case）。基本情况是递归停止的条件，而递归步骤则是函数调用自身的部分，它不断将问题规模缩小，直至达到基本情况。

在编写递归算法时，边界问题的处理尤其重要，因为错误的终止条件或者递归逻辑可能会导致无限递归或者栈溢出错误。在下一章中，我们将深入探讨Python环境下递归的机制及其限制，并提供一些解决这些问题的策略。

# 2. Python递归的机制与限制

Python 是一种高级编程语言，以其简洁的语法和强大的功能而闻名。递归是 Python 中处理复杂问题的一种常用技术，它允许函数调用自身来解决子问题。然而，递归在 Python 中也有其自身的机制和限制，理解这些内容对于编写高效和可维护的递归代码至关重要。

## 2.1 Python 递归的工作原理

Python 通过函数调用栈来支持递归函数的执行。每当一个函数被调用时，Python 解释器都会将其压入调用栈，然后执行函数中的代码。当函数执行完毕并返回时，它会从调用栈中弹出。在递归中，这个过程会重复进行，直到达到基本情况（base case），此时递归不再继续，函数开始返回并弹出调用栈。

### 2.1.1 调用栈的管理

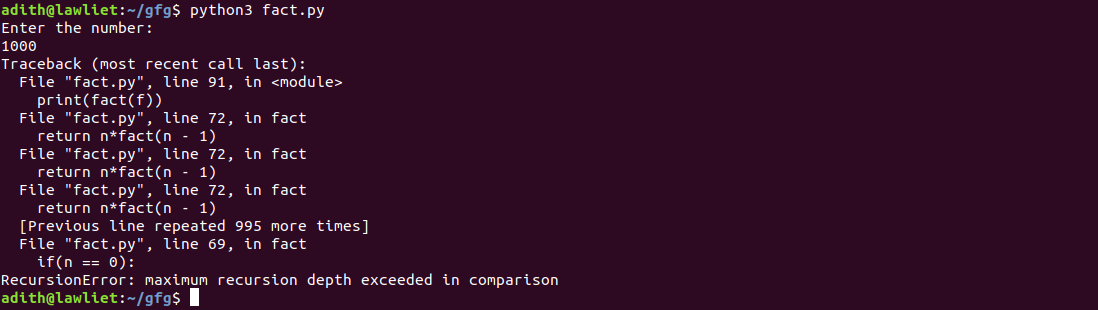
调用栈用于存储函数调用时的上下文信息，包括局部变量、参数、返回地址等。在 Python 中，每次递归调用都会消耗栈空间，递归深度受限于 Python 的最大递归深度限制，默认值为 1000。当达到这个限制时，Python 将抛出 `RecursionError`。

### 2.1.2 递归函数的设计原则

递归函数设计时需要考虑三个主要部分：基本情况、递归步骤和递归关系。基本情况是递归结束的条件，通常是一个最简单的问题实例；递归步骤是将问题分解为更小子问题的过程；递归关系则是如何将子问题的解组合起来得到原问题的解。

def factorial(n):
    # 基本情况
    if n == 0:
        return 1
    # 递归步骤
    else:
        return n * factorial(n - 1)

print(factorial(5))  # 输出: 120

在上述阶乘函数中，基本情况是 `n == 0` 时返回 1，递归步骤则是不断调用 `factorial` 函数自身直到基本情况。

## 2.2 Python 递归的性能考虑

递归算法通常比迭代算法的性能要差，主要原因是递归会带来额外的开销，比如函数调用和返回时的栈操作。此外，递归函数在执行时需要更多的内存空间，因为每次函数调用都需要保存其状态。

### 2.2.1 时间复杂度分析

递归算法的时间复杂度取决于递归的深度以及每次递归调用中处理的复杂度。例如，一个简单的线性递归算法，每次递归调用会生成一个新的子问题，其时间复杂度是 O(n)。

### 2.2.2 空间复杂度分析

递归的空间复杂度主要由递归深度决定。在最坏的情况下，如果递归没有减少问题的规模，空间复杂度将是 O(n)。然而，如果递归可以减少问题的规模，空间复杂度将取决于递归树的深度。

### 2.2.3 性能优化建议

为了优化递归算法的性能，可以考虑减少递归深度，例如使用尾递归优化。尾递归是一种特殊的递归形式，它允许语言实现使用迭代的方式进行优化。此外，可以考虑将递归转换为迭代，减少栈的使用和函数调用的开销。

## 2.3 Python 递归的限制

Python 中的递归受到最大递归深度的限制。当递归太深时，`RecursionError` 是不可避免的。为了避免这种情况，开发者需要对递归深度进行控制，或者使用其他技术如尾递归优化、迭代转换等策略来减少递归的使用。

### 2.3.1 最大递归深度的配置

在某些情况下，可以通过修改 Python 的最大递归深度来避免 `RecursionError`。这可以通过 `sys.setrecursionlimit` 函数实现，但这并不是一个推荐的做法，因为它可能会导致栈溢出并使程序崩溃。

import sys

# 修改最大递归深度
sys.setrecursionlimit(3000)

def recursive_function(n):
    # ... 递归逻辑 ...

### 2.3.2 递归限制的应对策略

当面临递归深度限制时，一个常见的策略是使用迭代来替代递归。这通常需要借助额外的数据结构，如栈或队列，来手动模拟递归调用栈的行为。这种方法可以有效地控制内存使用，避免栈溢出。

def iterative_factorial(n):
    result = 1
    for i in range(2, n + 1):
        result *= i
    return result

print(iterative_factorial(5))  # 输出: 120

在上述迭代版本的阶乘函数中，我们用一个 for 循环替代了递归调用，有效避免了递归深度限制的问题。

## 2.4 小结

Python 的递归机制提供了一种简洁明了的方法来解决复杂问题。理解其工作原理、性能考虑以及限制对于编写高效的递归代码至关重要。通过合理的设计递归函数、优化性能并注意最大递归深度限制，可以更好地利用递归解决实际问题，同时避免潜在的性能问题和错误。在下一章中，我们将探讨突破递归深度限制的策略，帮助开发者进一步提高递归算法的效率和性能。

# 3. 突破递归深度限制的策略

## 3.1 使用递归优化技术

### 3.1.1 尾递归优化

尾递归是一种特殊的递归形式，它的特点是函数的最后一个操作是一个递归调用。这种形式的递归在某些语言和编译器中可以被优化，避免了新的栈帧的创建，从而减少了递归深度限制的影响。尽管Python对尾递归优化支持不佳，但理解尾递归对于深入递归优化至关重要。

在支持尾递归优化的语言中，编译器或解释器可以将尾递归转换为一个简单的循环，因此不会增加额外的栈空间需求。以下是一个尾递归的例子：

def tail_recursive_factorial(n, accumulator=1):
    if n == 0:
        return accumulator
    else:
        return tail_recursive_factorial(n - 1, accumulator * n)

在这个例子中，递归调用是函数的最后一个操作，并且递归调用的结果直接作为函数返回值，这样编译器就可以进行优化。然而，由于Python解释器默认并不进行尾递归优化，上述代码并不会减少Python的递归深度限制。如果要实现尾递归优化，我们需要引入一个额外的步骤，例如使用装饰器来手动处理尾递归调用。

### 3.1.2 动态规划与记忆化搜索

动态规划是一种将复杂问题分解为简单子问题的优化方法，通过存储已解决子问题的解来避免重复计算，这是所谓的记忆化搜索。这种方法可以大幅降低时间复杂度，特别适用于具有重叠子问题的递归问题。

记忆化搜索通常与递归结合使用。我们使用一个字典或数组来存储子问题的解，当递归调用发生时，我们首先检查这个存储结构，如果解已存在则直接返回，否则递归计算并将结果存储起来。

例如，计算斐波那契数列的第n项的传统递归方法会导致指数级的时间复杂度，因为很多子问题被重复计算。而使用记忆化搜索后，时间复杂度可以降低到线性级别：

def memoized_fibonacci(n, memo=None):
    if memo is None:
        memo = {}
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = memoized_fibonacci(n - 1, memo) + memoized_fibonacci(n - 2, memo)
    return memo[n]

## 3.2 递归转换为迭代

### 3.2.1 迭代模拟递归过程

递归逻辑可以用迭代来模拟。迭代通常使用循环结构实现，相比递归，它避免了额