【递归转动态规划】：Python算法转换，从艺术到科学

# 1. 递归与动态规划基础

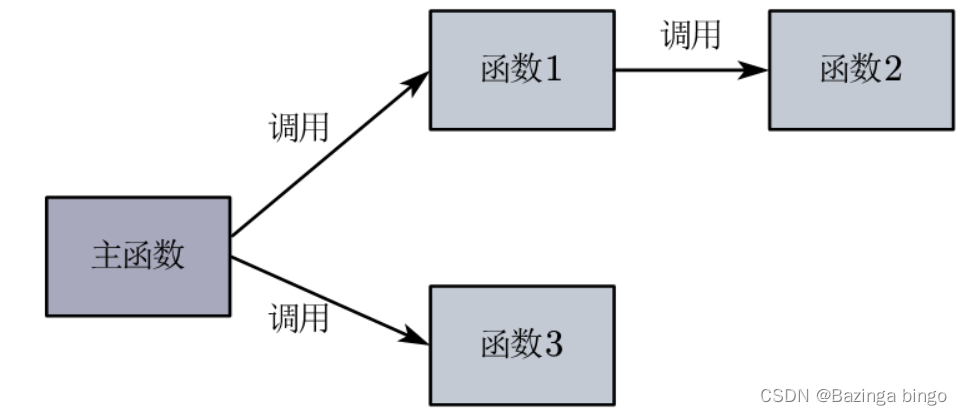
递归与动态规划是计算机科学中解决复杂问题的两大利器，它们在算法设计中扮演着重要角色。递归通过函数自身调用自身来解决问题，而动态规划则通过将复杂问题分解为更小的子问题来简化问题解决过程。

## 1.1 递归的基本概念

递归是一种常见的编程技术，其核心思想是将问题分解为更小的相似问题，并通过递归函数来解决。递归函数需要两个主要部分：基本情况（终止递归的条件）和递归步骤（函数调用自身）。

def recursive_function(parameters):
    if base_case_condition:  # 基本情况
        return base_case_value
    else:
        return recursive_function(modified_parameters)  # 递归步骤

## 1.2 动态规划的起源与原理

动态规划（Dynamic Programming, DP）由理查德·贝尔曼提出，用于解决最优化问题。它利用问题的重叠子问题和最优子结构特性，通过递推关系式来找出最优解。动态规划通常用于求解诸如最短路径、最小成本等问题。

## 1.3 递归与动态规划的联系

递归和动态规划之间的联系在于它们都采用分治策略来解决问题。递归往往直观且易于实现，但可能会导致重复计算和效率低下。动态规划通过记录子问题的解来避免重复计算，从而提高效率。两者之间的这种转换，通常需要对问题的理解和一定的算法技巧。

在接下来的章节中，我们将更深入地探索递归和动态规划的设计、分析和应用，并且提供实例来说明它们是如何工作的。

# 2. 递归算法的设计与分析

## 2.1 递归的原理和特性

### 2.1.1 递归的定义和工作原理
递归是一种常见的算法设计技巧，它允许一个函数调用自身来解决问题。递归函数通常包含两个基本要素：基准情形（base case）和递归情形（recursive case）。基准情形是递归的终止条件，它定义了最简单的可以立即解决的问题实例。递归情形则将复杂的问题分解为更小的子问题，并调用自身以求解。

递归的工作原理依赖于调用栈（call stack），每当一个函数被调用时，它的状态就会被压入调用栈，包括局部变量和返回地址。当函数返回时，它的状态会从调用栈中弹出。在递归中，每次递归调用都会创建函数的一个新实例，这些实例会在调用栈中形成一个调用链。当达到基准情形，递归调用开始回溯，逐层返回最终结果。

### 2.1.2 递归调用栈的理解和应用
递归调用栈是理解递归工作原理的关键。每个递归函数的调用都伴随着调用栈的更新，包括调用函数的返回地址、参数和局部变量。递归调用栈的使用遵循后进先出（LIFO）的原则。

为了更好地理解递归调用栈，我们可以考虑一个简单的递归函数的例子。以下是一个计算阶乘的递归函数：

def factorial(n):
    if n <= 1:  # 基准情形
        return 1
    else:  # 递归情形
        return n * factorial(n - 1)

当调用`factorial(3)`时，调用栈的变化如下：

调用栈: factorial(3)
         factorial(2)
         factorial(1)

在`factorial(1)`处达到基准情形并返回1，然后逐层回溯：

调用栈回溯: factorial(2) * 1 = 2
             factorial(3) * 2 = 6

最终返回结果6。

理解递归调用栈有助于分析递归算法的时间和空间复杂度，并帮助识别潜在的问题，如栈溢出错误。

## 2.2 递归算法的实例剖析

### 2.2.1 斐波那契数列的递归解法
斐波那契数列是一个经典的递归算法应用实例。斐波那契数列定义为：F(0)=0, F(1)=1, 对于 n > 1, F(n) = F(n-1) + F(n-2)。以下是一个递归实现的示例：

def fibonacci(n):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

在上述代码中，`fibonacci(n)`会递归地计算`fibonacci(n-1)`和`fibonacci(n-2)`直到达到基准情形。

### 2.2.2 汉诺塔问题的递归求解
汉诺塔问题是一个经典的递归问题，涉及将n个大小不同，穿孔的圆盘从一个塔座移动到另一个塔座，每次只能移动一个盘子，并且大盘子不能在小盘子上面。

递归解法可以描述为：
- 将n-1个盘子从起始柱子移动到辅助柱子。
- 将最大的盘子从起始柱子移动到目标柱子。
- 将n-1个盘子从辅助柱子移动到目标柱子。

以下是汉诺塔问题的递归解法代码：

def hanoi(n, source, target, auxiliary):
    if n > 0:
        hanoi(n - 1, source, auxiliary, target)  # 将n-1个盘子从起始柱子移动到辅助柱子
        print(f"Move disk {n} from {source} to {target}")  # 移动最大的盘子到目标柱子
        hanoi(n - 1, auxiliary, target, source)  # 将n-1个盘子从辅助柱子移动到目标柱子

在这个例子中，递归函数`hanoi`实现了汉诺塔问题的解决策略，并通过打印语句显示每次移动的动作。

## 2.3 递归到动态规划的必要性分析

### 2.3.1 递归的局限性和性能问题
虽然递归在概念上简单且易于实现，但它也存在局限性。递归的主要问题是性能问题，尤其是当递归深度较大时可能会导致栈溢出错误。此外，由于重复计算相同的子问题，递归算法可能非常低效。在斐波那契数列的例子中，朴素的递归解法的时间复杂度为O(2^n)，在n较大时计算效率很低。

### 2.3.2 动态规划的引入和优势
动态规划是优化递归算法的一种方法，它通过存储已经计算过的子问题的解来避免重复计算，从而显著提高效率。动态规划的关键思想是将问题分解为相互依赖的子问题，并按一定顺序解决问题。动态规划方法通常比递归方法更高效，时间复杂度可以从指数级别降低到多项式级别。

在下一章节中，我们将详细介绍动态规划的理论框架，包括其核心要素和优化技巧，并通过实例深入探讨递归向动态规划的转换过程。

# 3. 动态规划算法的理论框架

## 3.1 动态规划的四要素

### 3.1.1 状态定义和转移方程

动态规划的核心在于将复杂问题分解为更小的子问题，并将子问题的解存储起来，以便之后使用。这就需要我们定义状态来描述子问题，并建立状态之间的转移关系，即转移方程。

**状态定义** 是将问题分解为可以描述的最小单位，它通常是对原问题的某种表述方式的简化或特化。例如，在背包问题中，状态可以是当前考虑到的物品和剩余背包容量。

**转移方程** 则描述了如何从一个或多个较小的子问题的解推导出当前问题的解。例如，在零钱兑换问题中，转移方程可以表达为 `dp[i] = min(dp[i], dp[i - coins[j]] + 1)`，表示对于每个硬币，我们更新最小硬币数量的解。

在定义状态和转移方程时，需要明确：

1. 状态变量的含义和取值范围。
2. 状态转移的条件和结果。
3. 如何从已知的状态推导出新的状态。

### 3.1.2 初始条件和边界情况

**初始条件** 是动态规划中的基础情况，它提供了算法开始的起点。这通常是问题规模最小时的解，例如，背包问题中背包容量为0时，解为0。

**边界情况** 涉及到问题规模较大的时候，我们需要处理的特殊情况。这通常包括对问题空间的边界进行检查，并确保算法不会因为越界等问题而失败。在实现动态规划算法时，需要特别注意边界条件的设置，确保所有的状态转移都是有效的。

动态规划问题解决的关键在于能够准确地定义状态和转移方程，并合理处理初始条件和边界情况。下面给出一个经典的问题——斐波那契数列——的动态规划解法，以帮助理解上述概念。

def fibonacci(n):
    if n