【递归与大数据处理】：Python递归大数据问题，专家解决方案

# 1. 递归算法的原理与应用

## 1.1 递归算法的基本概念

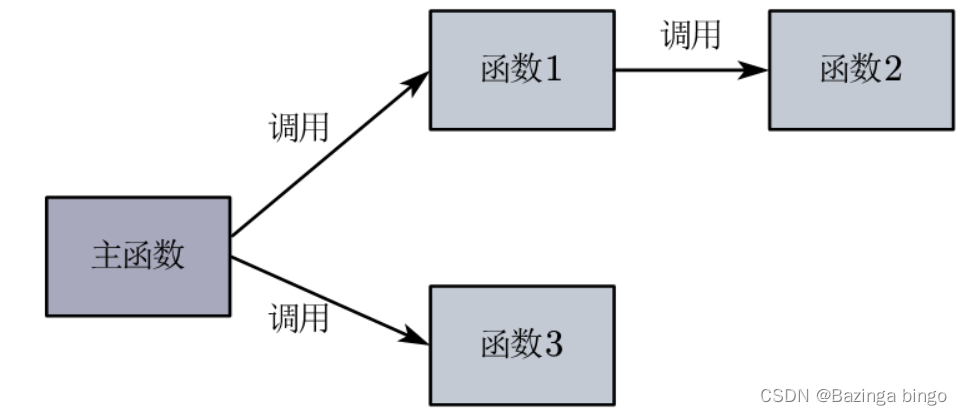
递归算法是一种在解决问题时反复调用自身的算法设计技术。它将问题分解为相似的子问题，直到达到一个易于解决的最小情况。递归算法的基本思想是将大问题拆分成小问题，直到问题简单到可以直接得到答案。

递归算法具有两个基本要素：
- **基本情况（Base Case）**：直接给出答案的最小子问题。
- **递归步骤（Recursive Step）**：将原问题分解为若干个更小的子问题，并递归地解决这些子问题。

例如，经典的斐波那契数列计算就是一个典型的递归问题，其定义如下：

fib(n) = fib(n-1) + fib(n-2) with base cases fib(0) = 0, fib(1) = 1

## 1.2 递归算法的适用场景

递归算法特别适合于解决那些问题可以分解为相似的子问题的情况，如树形结构的遍历（如文件系统的遍历）、图的搜索（深度优先搜索DFS）、排序算法（快速排序、归并排序）等。

递归算法的优点在于代码简洁、易于理解。但同时也存在缺点，例如当递归深度过大时可能导致栈溢出，递归的重复计算可能影响性能。

## 1.3 递归算法的效率优化

由于递归可能导致重复计算和过深的调用栈，对递归算法的效率优化是十分必要的。一些优化方法包括：
- **记忆化（Memoization）**：存储已经计算过的结果，避免重复计算。
- **尾递归优化（Tail Recursion）**：在某些语言中，编译器或解释器可以优化尾递归，避免增加新的栈帧。

通过这些方法，可以显著提高递归算法的运行效率，使其适用于更复杂的实际问题。

下面的章节将进一步探讨如何在Python中实现递归，并分析递归在大数据处理领域中的应用。

# 2. Python中的递归实现

递归是编程中的一个重要概念，它允许一个函数直接或间接地调用自身来解决问题。Python作为一门动态类型的高级编程语言，因其简洁的语法和强大的库支持，在递归实现方面表现得尤为出色。本章将深入探讨Python中的递归实现方法，并通过实例加深理解。

### 2.1 Python递归基础

#### 2.1.1 递归函数的概念和结构

递归函数是在函数内部调用自身的函数。在Python中，递归函数通常由两个主要部分组成：基本情况（Base Case）和递归情况（Recursive Case）。基本情况是递归停止的条件，确保递归能够收敛，防止无限递归的发生；递归情况则定义了如何将问题分解为更小的子问题，并调用自身以解决这些子问题。

def factorial(n):
    # 基本情况：当n等于1时，递归结束
    if n == 1:
        return 1
    else:
        # 递归情况：将n的阶乘转换为(n-1)的阶乘乘以n
        return n * factorial(n - 1)

在上面的阶乘函数中，基本情况是`n == 1`时返回1，递归情况是计算`n * factorial(n - 1)`直到基本情况满足。

#### 2.1.2 递归算法的适用场景

递归算法特别适合处理具有自然层级结构的问题，如树的遍历、分治算法和回溯算法等。递归能够简化代码逻辑，因为递归函数通常易于理解和编写。但递归也有局限性，例如性能问题和栈溢出的风险。

以下是递归算法适用的几种典型场景：
- 分治策略：如快速排序、归并排序等算法。
- 树形数据结构的操作：如二叉树的遍历。
- 动态规划：如计算斐波那契数列。
- 图论中的深度优先搜索（DFS）。

### 2.2 Python递归高级技巧

#### 2.2.1 尾递归优化

尾递归是一种特殊的递归形式，其中递归调用是函数体中的最后一个操作。尾递归优化是通过修改编译器或解释器来重新组织代码，使得递归调用可以利用当前的函数栈帧而不是创建一个新的，从而节省空间，避免栈溢出问题。然而，值得注意的是，Python的官方解释器CPython并不支持尾递归优化。

def tail_recursive_factorial(n, accumulator=1):
    if n == 0:
        return accumulator
    else:
        return tail_recursive_factorial(n - 1, accumulator * n)

上面的尾递归版本的阶乘函数，其最后一个操作是递归调用，理论上适合尾递归优化，但Python解释器不支持此优化。

#### 2.2.2 递归与迭代的比较

递归和迭代是解决问题的两种不同的方法。递归方法通常代码更简洁、易于理解，但可能会占用更多的内存空间和栈资源；迭代通常性能更好，更节省资源，但可能代码复杂度较高。选择递归还是迭代取决于具体问题和资源限制。

# 使用递归计算阶乘
def recursive_factorial(n):
    if n == 1:
        return 1
    else:
        return n * recursive_factorial(n - 1)

# 使用迭代计算阶乘
def iterative_factorial(n):
    result = 1
    for i in range(2, n + 1):
        result *= i
    return result

在阶乘的计算中，递归方法易于编写和理解，但迭代方法在性能上可能更优。

#### 2.2.3 避免递归的无限循环与栈溢出

由于递归函数可能会无限调用自身，因此必须谨慎设计递归算法，以确保它能够在有限的步骤内到达基本情况。避免无限循环的关键是确保每次递归调用都在朝着基本情况的方向迈进。另外，为了避免栈溢出，应该限制递归深度，或在递归实现中加入栈溢出的预防机制。

# 斐波那契数列的递归实现可能导致栈溢出
def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

# 优化后的斐波那契数列的迭代实现
def fibonacci_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

优化前的递归方法可能在计算较大的斐波那契数时造成栈溢出，而优化后的迭代方法则能够有效避免这一问题。

### 2.3 实例解析：递归在算法设计中的应用

#### 2.3.1 排序与搜索中的递归

递归在排序和搜索算法中有着广泛的应用。例如，快速排序和归并排序就是利用递归来实现的。这些算法通过递归将原问题分解为较小的子问题，然后合并子问题的结果来得到最终答案。

# 快速排序中的递归分区过程
def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x