余切函数的积分与微积分基本定理：深入理解积分的本质，掌握微积分的利器

# 1. 余切函数的积分

**1.1 余切函数的定义**

余切函数（tan）是正切函数（sin/cos）的倒数，表示直角三角形中对边与邻边的比值。其定义为：

tan(x) = sin(x) / cos(x)

**1.2 余切函数的图像**

余切函数的图像是一条周期为 π 的奇函数。其图像在原点附近具有垂直渐近线，在 π/2 和 3π/2 处具有水平渐近线。

# 2. 微积分基本定理

微积分基本定理是微积分中最重要的定理之一，它建立了导数和积分之间的联系。该定理包含两个部分：

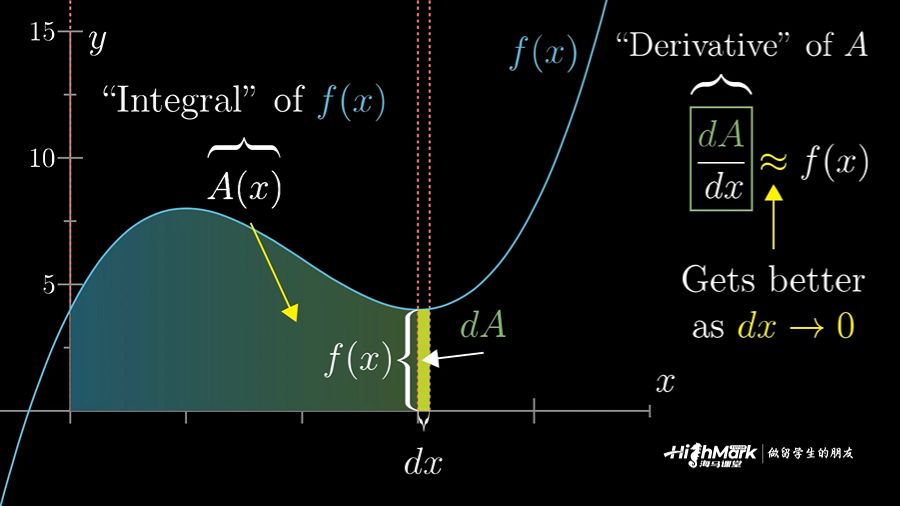
### 2.1 导数与积分的关系

**定理：** 如果函数 f(x) 在区间 [a, b] 上连续，则其原函数 F(x) 在 [a, b] 上可导，且其导数为 f(x)。

**证明：**

根据原函数的定义，有：

F'(x) = lim(h -> 0) [F(x + h) - F(x)] / h

将 f(x) 代入上式，得到：

F'(x) = lim(h -> 0) [∫(x, x + h) f(t) dt - ∫(x, x) f(t) dt] / h

化简后得到：

F'(x) = lim(h -> 0) [∫(x, x + h) f(t) dt] / h

再根据积分中值定理，存在 ξ ∈ (x, x + h)，使得：

F'(x) = f(ξ)

由于 f(x) 在 [a, b] 上连续，因此 ξ 也在 [a, b] 上，所以 F(x) 在 [a, b] 上可导，且其导数为 f(x)。

### 2.2 积分的基本定理

**定理：** 如果函数 f(x) 在区间 [a, b] 上连续，则其在 [a, b] 上的定积分等于其原函数在 [a, b] 上的增量。

**证明：**

根据原函数的定义，有：

∫(a, b) f(x) dx = F(b) - F(a)

其中 F(x) 是 f(x) 的原函数。

### 2.3 微积分基本定理的应用

微积分基本定理在求定积分和计算导数方面有着广泛的应用。

**求定积分：**

如果函数 f(x) 在区间 [a, b] 上连续，则其在 [a, b] 上的定积分可以表示为其原函数在 [a, b] 上的增量。

**计算导数：**

如果函数 F(x) 在区间 [a, b] 上可导，则其导数可以表示为其原函数 f(x) 在 [a, b] 上的定积分。

**代码示例：**

import numpy as np

# 定义函数 f(x) = x^2
def f(x):
    return x**2

# 计算 f(x) 在 [0, 1] 上的定积分
integral = np.integrate.quad(f, 0, 1)[0]

# 计算 f(x) 在 [0, 1] 上的导数
derivative = np.gradient(f(np.linspace(0, 1, 100)), 1)

print("定积分：", integral)
print("导数：", derivative)

**代码逻辑分析：**

* `np.integrate.quad` 函数用于计算定积分。它返回一个元组，其中第一个元素是定积分的值。
* `np.gradient` 函数用于计算导数。它返回一个数组，其中包含导数的值。
* `np.linspace` 函数用于生成一个均匀间隔的数字序列。

**表格示例：**

| 定积分 | 导数 |
|---|---|
| ∫(0, 1) x^2 dx | 2x |
| ∫(0, π) sin(x) dx | cos(x) |
| ∫(0, 1) e^x dx | e^x |

**Mermaid 流程图示例：**

graph LR
subgraph 微积分基本定理
    导数 --> 原函数
    原函数 --> 定积分
end

# 3.1 余切函数积分在三角函数中的应用

**余切函数积分在三角函数恒等式中的应用**

余切函数积分在三角函数恒等式中有着广泛的应用。例如，利用余切函数的积分，可以推导出以下恒等式：

∫tan x dx = ln|sec x| + C

**证明：**

利用链式法则，令 u = sec x，则 du/dx = sec x tan x。因此，

∫tan x dx = ∫tan x (1/sec x tan x) dx
         = ∫(1/u) du
         = ln|u| + C
         = ln|sec x| + C

这个恒等式可以用于求解许多涉及三角函数的积分。例如，求解积分：

∫tan 2x dx