KNN算法与其他机器学习算法的对比分析

# 1. 算法原理

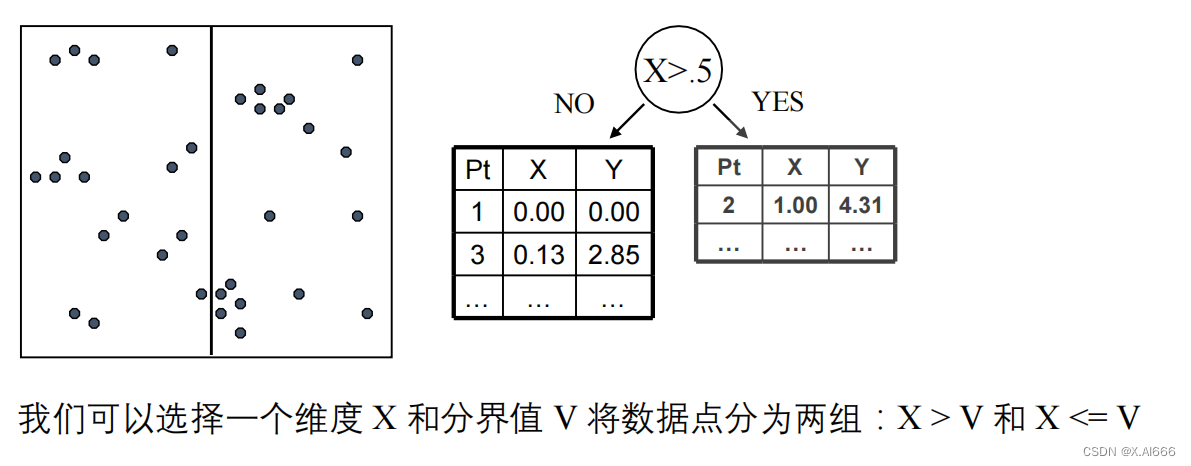
在机器学习领域，算法是指解决问题的一系列规则和步骤。机器学习算法是让计算机根据数据自动学习和改进性能的方法。K最近邻（KNN）算法是一种简单且常用的监督学习算法，其原理基于特征空间中样本点之间的距离进行分类。KNN算法的核心概念是基于周围K个最近邻居的投票来确定样本的类别。通过计算不同样本点之间的距离，KNN算法可以帮助我们进行分类和预测任务。算法的核心思想简单直观，适用于各种数据类型和领域，为初学者入门机器学习提供了一个良好的起点。随着对KNN算法原理的深入理解，我们可以更好地应用和优化该算法。

# 2. KNN算法参数调优与性能优化

### 2.1 KNN算法中的K值选择

在KNN算法中，K值的选择对分类结果具有重要影响。K值过小容易受噪声影响，导致过拟合，而K值过大则可能忽略了样本之间的局部特征。通常通过交叉验证选择最佳的K值，避免模型过分简单或过于复杂。

# 交叉验证选择最优K值
from sklearn.model_selection import cross_val_score
import numpy as np

k_range = range(1, 31)
k_scores = []
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn, X_train, y_train, cv=10, scoring='accuracy')
    k_scores.append(scores.mean())

best_k = k_range[np.argmax(k_scores)]

### 2.2 特征标准化对KNN算法的影响

KNN算法基于距离计算相似度，不同特征的数值范围差异大会导致某些特征对距离计算影响过大。因此，在应用KNN算法前，需对特征进行标准化处理，使各特征权重相同，提高模型的性能和泛化能力。

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

### 2.3 距离度量指标选择

KNN算法常用的距离度量有欧氏距离、曼哈顿距离、闵可夫斯基距离等。选择合适的距离度量方式能够更准确地衡量样本间的距离，从而提高模型的分类性能。