深入解读KNN算法中的投票机制

# 1. 理解K近邻算法
- **1.1 KNN算法概述**
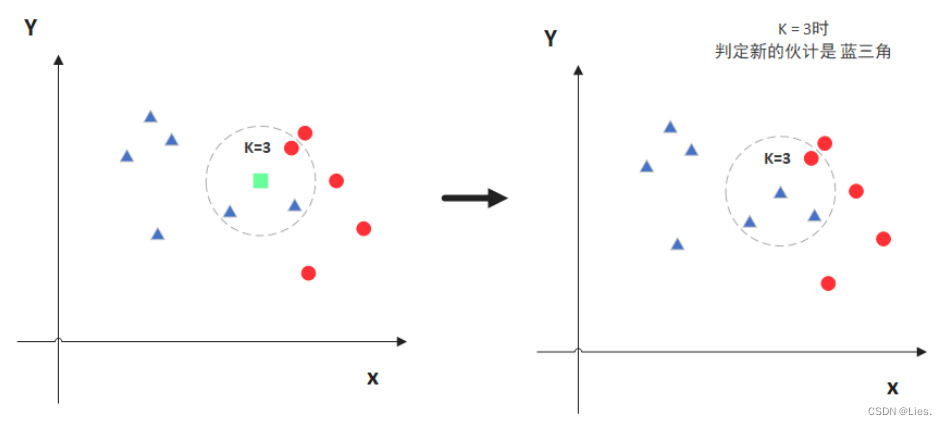
K近邻算法是一种简单而有效的监督学习算法，通过计算待分类数据点与已知数据点的距离来进行分类。
- **1.2 KNN算法流程**
KNN算法主要包含三个步骤：计算距离、确定K值和投票选举。首先计算待分类数据点与已知数据点的距离，然后确定K个最近邻居，最后通过投票选举确定待分类数据点所属类别。这种算法直观简单，易于理解和实现。

# 2. KNN算法中的距离计算

#### 2.1 欧氏距离

**2.1.1 定义**

欧氏距离是最常见的距离度量方法，用于衡量两个点之间的直线距离。

**2.1.2 计算公式**

在二维空间中，两点$(x_1, y_1), (x_2, y_2)$之间的欧氏距离为：
\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

**2.1.3 应用场景**

欧氏距离常用于数据挖掘、模式识别等领域，在KNN算法中广泛应用于分类和回归问题中。

#### 2.2 曼哈顿距离

**2.2.1 定义**

曼哈顿距离又称为城市街区距离，表示两点在标准坐标系上沿网格状路径行走的距离总和。

**2.2.2 计算公式**

在二维空间中，两点$(x_1, y_1), (x_2, y_2)$之间的曼哈顿距离为：
|x_2 - x_1| + |y_2 - y_1|

**2.2.3 应用场景**

曼哈顿距离常用于城市交通规划、计算机视觉等领域，在KNN算法中可用于处理维度较高的数据集。

#### 2.3 切比雪夫距离

**2.3.1 定义**

切比雪夫距离是距离空间中的一种度量方式，表示两个向量在各个坐标轴上差值的绝对值的最大值。

**2.3.2 计算公式**

在二维空间中，两点$(x_1, y_1), (x_2, y_2)$之间的切比雪夫距离为：
\max(|x_2 - x_1|, |y_2 - y_1|)

**2.3.3 应用场景**

切比雪夫距离常用于棋盘距离的计算、异常检测等领域，在KNN算法中可应用于特征值为离散值的情况。

通过以上对欧氏距离、曼哈顿距离和切比雪夫距离的介绍，我们能更全面地理解KNN算法中距离计算的本质和多样性。

# 3. 选择最佳K值

K近邻算法中的K值选择至关重要，其直接影响了模型的性能和泛化能力。在本章节中，我们将深入探讨如何选择最佳的K值，以提高算法的准确性和可靠性。

#### 3.1 K值的意义

K值是指在K近邻算法中选择邻居的数量。不同的K值会导致不同的预测结果，因此选取合适的K值至关重要。我们将首先讨论不同K值的影响，然后介绍寻找最佳K值的方法。

*3.1.1 不同K值的影响*
在K近邻算法中，较小的K值会对模型产生较大的波动，可能会使模型对噪声点敏感；而较大的K值通常会使预测结果平滑化，但可能忽略了局部结构的细节。

*3.1.2 寻找最佳K值的方法*
为了找到最佳的K值，可以采用交叉验证方法。通过交叉验证，我们可以评估不同K值下模型的性能表现，从而选择最优的K值。

#### 3.2 交叉验证

交叉验证是一种常用的模型评估方法，可以帮助我们选择最佳的K值。在本节中，我们将介绍k折交叉验证和留一交叉验证两种常见的交叉验证方法，并比较它们的优缺点。

*3.2.1 k