揭秘线性搜索算法：从原理到实战应用，让你成为搜索高手

# 1. 线性搜索算法概述

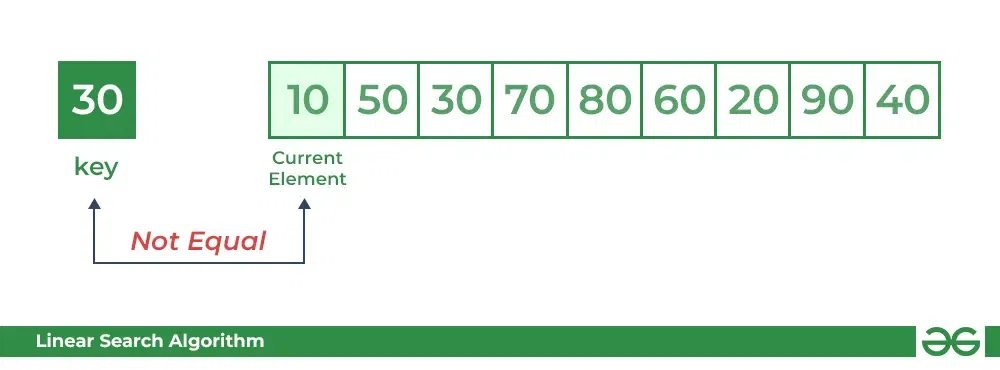
线性搜索算法是一种最简单的搜索算法，它通过逐个比较目标元素与列表中的每个元素来查找目标元素。它具有以下特点：

- **简单易懂：**线性搜索的实现非常简单，易于理解和实现。
- **时间复杂度高：**线性搜索的时间复杂度为 O(n)，其中 n 是列表中的元素数量。这使得它对于大型列表来说效率低下。
- **广泛适用：**线性搜索可以应用于任何类型的数据结构，包括数组、链表和集合。

# 2. 线性搜索算法的理论基础

### 2.1 线性搜索的定义和原理

线性搜索，又称顺序搜索，是一种最简单的搜索算法。其原理是逐个遍历序列中的元素，并与给定的目标值进行比较，直到找到目标值或遍历完整个序列。

### 2.2 线性搜索的时间复杂度分析

线性搜索的时间复杂度为 O(n)，其中 n 为序列的长度。这是因为在最坏的情况下，需要遍历整个序列才能找到目标值。

def linear_search(arr, target):
    """
    线性搜索算法

    Args:
        arr: 待搜索的序列
        target: 目标值

    Returns:
        目标值在序列中的索引，若不存在则返回 -1
    """

    for i in range(len(arr)):
        if arr[i] == target:
            return i

    return -1

**逻辑分析：**

该代码逐个遍历序列中的元素，并与目标值进行比较。如果找到目标值，则返回其索引；否则，遍历完整个序列后返回 -1。

**参数说明：**

* `arr`：待搜索的序列
* `target`：目标值

**时间复杂度：**

O(n)，其中 n 为序列的长度。

# 3. 线性搜索算法的实践应用

### 3.1 Python 中线性搜索算法的实现

在 Python 中，我们可以使用 `in` 运算符来实现线性搜索。`in` 运算符检查给定元素是否在可迭代对象中，如果存在，则返回 `True`，否则返回 `False`。

def linear_search_python(arr, target):
    """
    在 Python 中使用线性搜索算法查找目标元素。

    参数：
        arr (list): 要搜索的数组。
        target (any): 要查找的目标元素。

    返回：
        int: 目标元素在数组中的索引，如果不存在则返回 -1。
    """

    for i in range(len(arr)):
        if arr[i] == target:
            return i

    return -1

**代码逻辑分析：**

* 遍历数组 `arr` 中的每个元素。
* 对于每个元素，检查它是否等于目标元素 `target`。
* 如果找到目标元素，则返回其索引。
* 如果遍历完整个数组都没有找到目标元素，则返回 -1。

**参数说明：**

* `arr`：要搜索的数组。
* `target`：要查找的目标元素。

### 3.2 Java 中线性搜索算法的实现

在 Java 中，我们可以使用 `for` 循环来实现线性搜索。

public static int linearSearchJava(int[] arr, int target) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == target) {
            return i;
        }
    }

    return -1;
}

**代码逻辑分析：**

* 遍历数组 `arr` 中的每个元素。
* 对于每个元素，检查它是否等于目标元素 `target`。
* 如果找到目标元素，则返回其索引。
* 如果遍历完整个数组都没有找到目标元素，则返回 -1。

**参数说明：**

* `arr`：要搜索的数组。
* `target`：要查找的目标元素。

# 4. 线性搜索算法的优化和拓展

### 4.1 线性搜索算法的优化技巧

#### 4.1.1 哨兵技术

哨兵技术是一种优化线性搜索算法的技巧，它通过在数组末尾添加一个特殊元素（哨兵）来避免在搜索过程中进行不必要的比较。

**代码块：**

def linear_search_with_sentinel(arr, target):
    # 添加哨兵
    arr.append(target)
    i = 0
    while arr[i] != target:
        i += 1
    if i < len(arr) - 1:
        return i
    else:
        return -1

**逻辑分析：**

* 在数组末尾添加哨兵，哨兵的值等于目标值。
* 从数组的第一个元素开始搜索，如果当前元素不等于目标值，则继续搜索下一个元素。
* 当遇到哨兵时，说明目标值不在数组中，返回-1。
* 如果在哨兵之前找到目标值，则返回目标值在数组中的索引。

#### 4.1.2 移动到前面

移动到前面是一种优化线性搜索算法的技巧，它通过将最近访问过的元素移动到数组前面来减少搜索时间。

**代码块：**

def linear_search_with_move_to_front(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            # 将目标元素移动到数组前面
            arr[i], arr[0] = arr[0], arr[i]
            return i
    return -1

**逻辑分析：**

* 遍历数组，如果找到目标值，则将目标值移动到数组的第一个元素。
* 这样做可以提高下次搜索同一目标值的效率，因为目标值现在位于数组的开头。
* 如果在遍历过程中没有找到目标值，则返回-1。

### 4.2 线性搜索算法的拓展应用

#### 4.2.1 字符串搜索

线性搜索算法可以用来在字符串中搜索子字符串。

**代码块：**

def string_search(string, substring):
    for i in range(len(string) - len(substring) + 1):
        if string[i:i + len(substring)] == substring:
            return i
    return -1

**逻辑分析：**

* 遍历字符串，从第一个字符开始，直到字符串的长度减去子字符串的长度。
* 对于每个字符，检查子字符串是否与字符串的当前子串匹配。
* 如果匹配，则返回子字符串在字符串中的起始索引。
* 如果没有匹配，则继续搜索下一个字符。

#### 4.2.2 查找最大值和最小值

线性搜索算法可以用来查找数组中的最大值和最小值。

**代码块：**

def find_max_and_min(arr):
    max_value = arr[0]
    min_value = arr[0]
    for i in range(1, len(arr)):
        if arr[i] > max_value:
            max_value = arr[i]
        if arr[i] < min_value:
            min_value = arr[i]
    return max_value, min_value

**逻辑分析：**

* 遍历数组，并初始化最大值和最小值。
* 对于每个元素，如果它大于当前最大值，则更新最大值。
* 如果它小于当前最小值，则更新最小值。
* 遍历完成后，返回最大值和最小值。

# 5. 线性搜索算法与其他搜索算法的比较

### 5.1 线性搜索与二分搜索的比较

**原理对比：**

| 特征 | 线性搜索 | 二分搜索 |
|---|---|---|
| 搜索范围 | 从头到尾遍历 | 将搜索范围不断缩小 |
| 数据结构 | 无序数组 | 有序数组 |
| 时间复杂度 | O(n) | O(log n) |

**适用场景：**

* 线性搜索适用于数据量较小或数组无序的情况。
* 二分搜索适用于数据量较大且数组有序的情况。

### 5.2 线性搜索与哈希表的比较

**原理对比：**

| 特征 | 线性搜索 | 哈希表 |
|---|---|---|
| 数据结构 | 数组 | 哈希表 |
| 查找方式 | 遍历数组 | 根据哈希函数计算键值 |
| 时间复杂度 | O(n) | O(1)（平均情况下） |

**适用场景：**

* 线性搜索适用于数据量较小或数组无序的情况。
* 哈希表适用于数据量较大且需要快速查找的情况，例如键值对存储。

### 比较总结

| 特征 | 线性搜索 | 二分搜索 | 哈希表 |
|---|---|---|---|
| 适用数据结构 | 无序数组 | 有序数组 | 哈希表 |
| 时间复杂度 | O(n) | O(log n) | O(1)（平均情况下） |
| 适用场景 | 数据量较小或无序数组 | 数据量较大且有序数组 | 数据量较大且需要快速查找 |