Matlab小波变换在语音处理中的奇效:降噪与特征提取秘诀
发布时间: 2024-06-11 00:42:33 阅读量: 98 订阅数: 43 


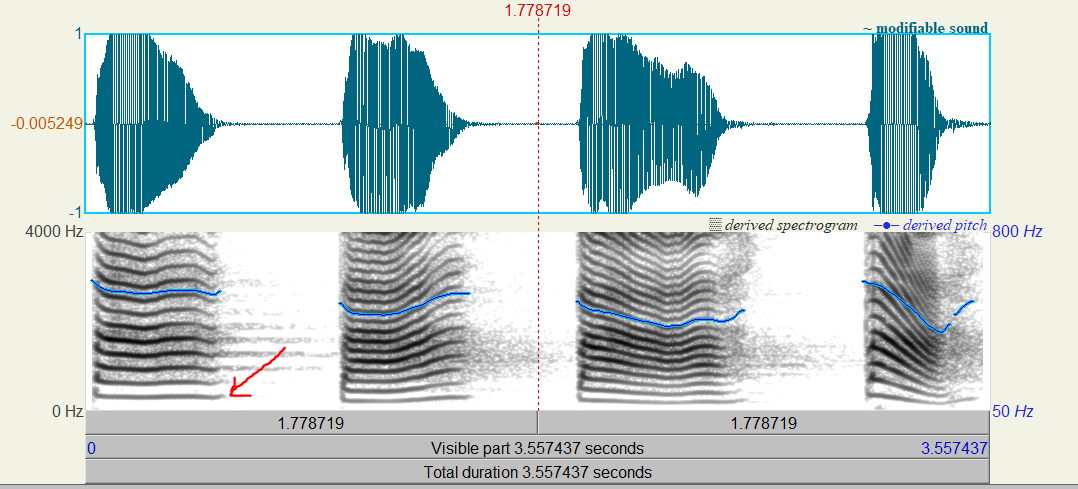
小波变换在语音去噪处理中的应用
# 1. 小波变换基础理论
小波变换是一种时频分析技术,它将信号分解为一系列小波函数的线性组合。小波函数是一个局部化的、振荡的函数,具有良好的时频特性。通过调整小波函数的尺度和位置,可以对信号进行多尺度的分析,提取不同频率和时间范围内的特征。
小波变换具有以下特点:
- 多尺度分析:小波变换可以对信号进行多尺度分解,提取不同频率和时间范围内的特征。
- 局部化:小波函数是局部化的,可以对信号的局部特征进行分析。
- 时频分析:小波变换可以同时分析信号的时域和频域特征。
# 2. 小波变换在语音降噪中的实践应用
### 2.1 小波降噪的基本原理
#### 2.1.1 小波分解与重构
小波降噪的基本原理是利用小波变换将噪声信号分解为不同尺度的子带,然后对不同子带的信号进行处理,最后将处理后的子带信号重构为降噪后的信号。
小波分解是一种时频分析技术,它可以将信号分解为一系列不同尺度和频率的子带。在小波分解过程中,原始信号被通过一系列小波基函数,这些小波基函数具有不同的尺度和频率。不同尺度的子带对应于不同频率范围的信号。
小波重构是将小波分解后的子带信号重新组合成原始信号的过程。在小波重构过程中,不同尺度的子带信号被通过逆小波基函数进行重构。
#### 2.1.2 降噪算法的选取
在小波降噪中,常用的降噪算法有软阈值法、硬阈值法和维纳滤波法。
* **软阈值法:**软阈值法是一种非线性降噪算法,它将小波分解后的子带信号中的幅度小于阈值的部分置为零,大于阈值的部分则减去阈值。软阈值法的降噪效果较好,但它会引入一定的失真。
* **硬阈值法:**硬阈值法是一种非线性降噪算法,它将小波分解后的子带信号中的幅度小于阈值的部分置为零,大于阈值的部分保留不变。硬阈值法的降噪效果较差,但它不会引入失真。
* **维纳滤波法:**维纳滤波法是一种线性降噪算法,它利用噪声信号的统计特性来估计噪声信号,然后将噪声信号从原始信号中减去。维纳滤波法的降噪效果较好,但它需要知道噪声信号的统计特性。
### 2.2 Matlab小波降噪实践
#### 2.2.1 噪声信号的生成
在Matlab中,可以使用`randn`函数生成噪声信号。`randn`函数可以生成服从正态分布的随机数。
```matlab
% 采样频率
fs = 16000;
% 信号长度
N = 1024;
% 生成正态分布噪声信号
noise = randn(1, N);
```
#### 2.2.2 降噪算法的实现与效果评估
在Matlab中,可以使用`wavedec`函数进行小波分解,使用`waverec`函数进行小波重构。
```matlab
% 小波分解
[cA, cD] = wavedec(noise, 5, 'db4');
% 软阈值降噪
threshold = 0.1;
cD_denoised = wthresh(cD, 's', threshold);
% 小波重构
noise_denoised = waverec([cA, cD_denoised], 'db4');
% 计算信噪比
snr_noise = 10 * log10(var(noise) / var(noise - noise_denoised));
% 绘制降噪前后信号的频谱
figure;
subplot(2, 1, 1);
plot(abs(fft(noise)));
titl
```
0
0





