Matlab小波变换的常见问题解答：解决实际应用中的难题，畅通无阻

# 1. Matlab小波变换概述**

小波变换是一种时频分析技术，它可以将信号分解为一系列小波函数的线性组合。小波函数是一种具有局部化和振荡性的函数，它可以有效地捕捉信号的局部特征。

在Matlab中，小波变换可以通过wavelet函数实现。wavelet函数接受一个信号向量和一个小波函数作为输入，并返回信号的小波分解。小波分解是一个多尺度的表示，它包含了信号在不同频率和时间尺度上的信息。

小波变换在信号和图像处理中有着广泛的应用。它可以用于降噪、特征提取、图像增强和信号分类等任务。

# 2. Matlab小波变换的理论基础

### 2.1 小波变换的基本原理

小波变换是一种时频分析技术，它将信号分解成一系列的小波函数，每个小波函数都具有不同的频率和时间范围。与傅里叶变换不同，小波变换可以同时在时域和频域上分析信号，从而能够捕捉到信号的局部特征。

小波变换的基本原理是将信号与一个称为母小波的函数进行卷积。母小波是一个具有有限能量和平均值为零的函数。通过改变母小波的尺度和平移，可以生成一系列的小波函数，这些小波函数可以用来分析信号的不同频率和时间范围。

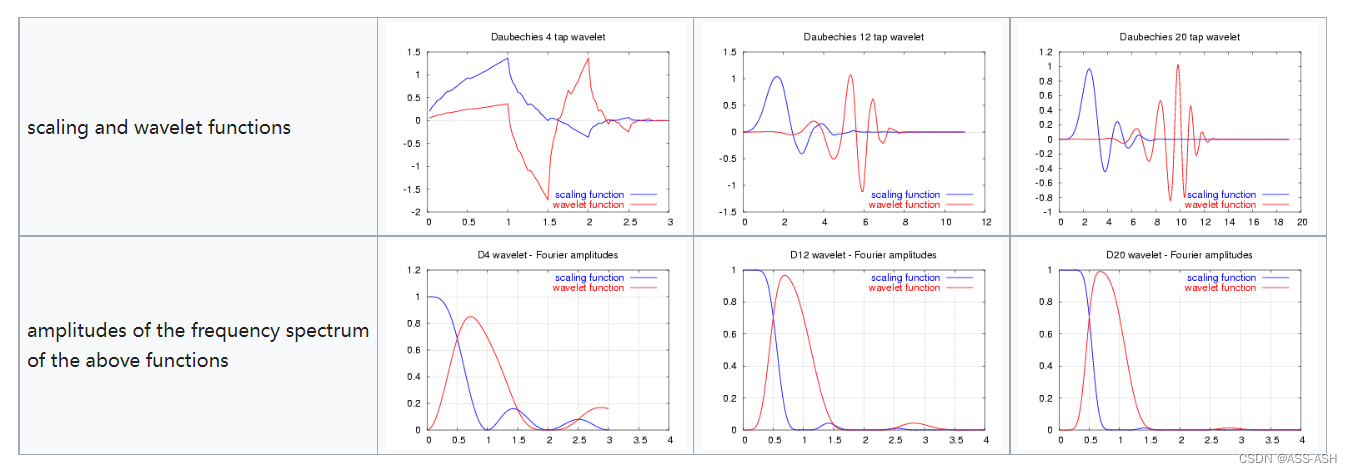
### 2.2 小波函数和尺度函数

**小波函数**是由母小波通过平移和尺度变换得到的：

psi(t) = 1 / sqrt(a) * psi((t - b) / a)

其中：

* `psi(t)` 是小波函数
* `psi` 是母小波
* `a` 是尺度因子
* `b` 是平移因子

**尺度函数**是母小波的平移和尺度变换：

phi(t) = 1 / sqrt(a) * phi((t - b) / a)

其中：

* `phi(t)` 是尺度函数
* `phi` 是母小波
* `a` 是尺度因子
* `b` 是平移因子

小波函数和尺度函数构成了小波变换的基础。小波函数用于分析信号的高频分量，而尺度函数用于分析信号的低频分量。

### 2.3 小波变换的算法和实现

小波变换可以通过离散小波变换（DWT）算法实现。DWT算法将信号分解成一系列的近似系数和细节系数。近似系数表示信号的低频分量，而细节系数表示信号的高频分量。

DWT算法的流程如下：

1. 将信号与低通滤波器和高通滤波器进行卷积。
2. 将卷积结果下采样。
3. 重复步骤1和步骤2，直到达到所需的分解层数。

Matlab中提供了 `wavedec` 函数和 `waverec` 函数来实现DWT算法。`wavedec` 函数将信号分解成近似系数和细节系数，而 `waverec` 函数将近似系数和细节系数重构为原始信号。

% 信号分解
[cA, cD] = wavedec(signal, level, wavelet);

% 信号重构
reconstructedSignal = waverec(cA, cD, wavelet);

其中：

* `signal` 是要分解的信号
* `level` 是分解层数
* `wavelet` 是母小波
* `cA` 是近似系数
* `cD` 是细节系数
* `reconstructedS