Matlab小波变换实战：图像处理的降噪与边缘检测秘籍

# 1. 小波变换理论基础**

小波变换是一种时频分析技术，它通过将信号分解为一组基函数（小波）来揭示信号的局部时频特性。小波具有良好的时域和频域局部化特性，使得它能够同时捕捉信号的瞬态和频率变化。

小波变换的数学表示为：

WT(a, b) = ∫ f(t) * ψ(a, b - t) dt

其中，*f(t)* 是信号，*ψ(a, b - t)* 是小波基，*a* 是尺度参数，*b* 是平移参数。通过改变尺度和平移参数，可以对信号进行多尺度分析，从而提取不同尺度上的特征。

# 2.1 图像降噪的原理和方法

### 2.1.1 降噪算法的分类

图像降噪算法主要分为两类：空间域算法和频域算法。

**空间域算法**直接对图像像素进行操作，例如：均值滤波、中值滤波、高斯滤波等。这些算法简单易行，但降噪效果有限，容易造成图像模糊。

**频域算法**将图像从空间域变换到频域，然后对频域中的噪声分量进行处理。小波变换就是一种典型的频域降噪算法。

### 2.1.2 小波变换在降噪中的优势

小波变换在图像降噪中具有以下优势：

* **多尺度分析：**小波变换可以将图像分解成不同尺度的子带，从而可以针对不同尺度的噪声进行处理。
* **时频局部化：**小波变换具有时频局部化的特性，可以有效地去除图像中的局部噪声，同时保留图像的边缘和纹理等重要信息。
* **自适应性：**小波变换可以根据图像的特征自适应地选择小波基和分解层数，从而实现针对不同图像的优化降噪效果。

## 2.2 小波变换降噪的实现步骤

### 2.2.1 小波基的选择

小波基的选择对降噪效果至关重要。常用的降噪小波基包括：

* Daubechies小波
* Symlets小波
* Coiflets小波

选择小波基时，需要考虑小波基的正交性、紧支性、分解深度等因素。

### 2.2.2 分解与重建

小波变换降噪的步骤如下：

1. **正向小波变换：**将原始图像分解成不同尺度的子带。
2. **阈值处理：**对每个子带中的系数进行阈值处理，去除噪声分量。
3. **反向小波变换：**将处理后的子带重建为降噪后的图像。

### 2.2.3 阈值选取和反变换

阈值选取是影响降噪效果的关键参数。常用的阈值选取方法包括：

* **软阈值：**将小于阈值的系数置为0，大于阈值的系数减去阈值。
* **硬阈值：**将小于阈值的系数置为0，大于阈值的系数保留不变。

反变换时，需要根据阈值处理后的系数重建图像。常用的重建方法包括：

* **正交小波重建：**使用正交小波基重建图像。
* **双线性插值重建：**使用双线性插值法重建图像。

# 3. 小波变换在图像边缘检测中的实践**

### 3.1 图像边缘检测的原理和方法

**3.1.1 边缘检测算法的分类**

图像边缘检测算法主要分为两类：

- **基于梯度的算法：**利用图像灰度值的变化率来检测边缘，如 Sobel 算子、Canny 算子。
- **基于区域的算法：**将图像分割成不同的区域，然后根据区域之间的差异来检测边缘，如区域生长算法、分水岭算法。

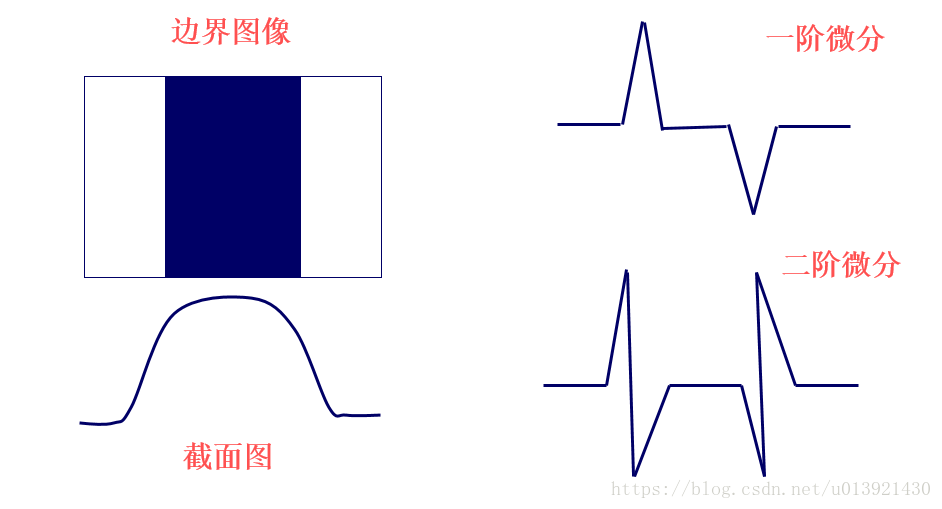
**3.1.2 小波变换在边缘检测中的作用**

小波变换具有良好的时频局部化特性，可以同时在时域和频域上分析信号。在图像边缘检测中，小波变换可以有效提取图像中不同尺度和方向上的边缘信息。

### 3.2 小波变换边缘检测的实现步骤

**3.2.1 小波基的选择**

小波基的选择对边缘检测效果有较大影响。常用的边缘检测小波基包括：

- Haar 小波：简单易用，但方向性较差。
- Daubechies 小波：具有较好的方向性和紧支撑性。
- Symlet 小波：具有较好的对称性和紧支撑性。

**3.2.2 分解与重构**

小波边缘检测的过程主要包括以下步骤：

1. 对图像进行小波分解，得到不同尺度和方向上的小波系数。
2. 对小波系数进行阈值处理，去除噪声和冗余信息。
3. 对阈值处理后的系数进行反变换，得到边缘增强后的图像。

**3.2.3 边缘提取和后处理**

边缘提取可以通过设置合适的阈值来实现。阈值过高会导致边缘检测不完整，阈值过低会导致噪声干扰。

边缘提取后，通常需要进行后处理以去除孤立点和虚假边缘。常用的后处理方法包括：

- 连通域分析：去除面积较小的连通域。
- 形态学处理：利用形态学算子对边缘进行细化和填充。

# 4. 小波变换在图像处理中的进阶应用

### 4.1 图像融合

#### 4.1.1 图像融合的原理和方法

图像融合是一种将来自不同来源或不同时间点的图像组合成一张新图像的技术。它在许多领域都有应用，如医学成像、遥感和计算机视觉。

图像融合算法通常分为以下几个步骤：

1. **配准：**将不同图像对齐到相同的空间坐标系。
2. **融合：**将对齐的图像融合成一张新图像。
3. **后处理：**对融合后的图像进行增强或降噪。

图像融合的常见方法包括：

- **平均融合：**将不同图像的像素值取平均。
- **加权平均融合：**将不同图像的像素值加权平均，其中权重可以根据图像质量或其他因素确定。
- **小波融合：**利用小波变换将图像分解成不同尺度的子带，然后对每个子带进行融合。

#### 4.1.2 小波变换在图像融合中的应用

小波变换在图像融合中具有以下优势：

- **多尺度分析：**小波变换可以将图像分解成不同尺度的子带，这使得可以针对不同尺度的图像特征进行融合。
- **方向性：**小波变换可以捕获图像中的方向性信息，这有助于保留融合后图像的边缘和纹理。
- **抗噪性：**小波变换具有抗噪性，可以有效去除图像中的噪声。

小波融合算法通常采用以下步骤：

1. 将不同图像分解成小波子带。
2. 对每个子带进行融合。
3. 重构融合后的图像。

### 4.2 图像增强

#### 4.2.1 图像增强的原理和方法

图像增强是一种通过处理图像数据来改善图像质量的技术。它可以用于增强图像的对比度、亮度、锐度或其他特征。

图像增强算法通常分为以下几个步骤：

1. **预处理：**对图像进行预处理，如去噪和配准。
2. **增强：**使用各种算法对图像进行增强。
3. **后处理：**对增强后的图像进行后处理，如锐化和对比度调整。

图像增强的常见方法包括：

- **直方图均衡化：**调整图像的直方图以改善对比度。
- **伽马校正：**调整图像的伽马值以改变亮度。
- **锐化：**使用卷积核或其他算法增强图像的边缘。

#### 4.2.2 小波变换在图像增强中的应用

小波变换在图像增强中具有以下优势：

- **多尺度分析：**小波变换可以将图像分解成不同尺度的子带，这使得可以针对不同尺度的图像特征进行增强。
- **方向性：**小波变换可以捕获图像中的方向性信息，这有助于保留增强后图像的边缘和纹理。
- **抗噪性：**小波变换具有抗噪性，可以有效去除图像中的噪声。

小波增强算法通常采用以下步骤：

1. 将图像分解成小波子带。
2. 对每个子带进行增强。
3. 重构增强后的图像。

# 5. Matlab中实现小波变换的实战案例

### 5.1 图像降噪实战

#### 5.1.1 代码实现

% 读取图像
img = imread('noisy_image.jpg');

% 将图像转换为灰度图
img_gray = rgb2gray(img);

% 选择小波基
wavelet_name = 'haar';

% 分解图像
[cA, cH, cV, cD] = dwt2(img_gray, wavelet_name);

% 选择阈值方法
threshold_method = 'soft';

% 根据阈值方法选择阈值
if strcmp(threshold_method, 'soft')
    threshold = 0.1;
elseif strcmp(threshold_method, 'hard')
    threshold = 0.2;
end

% 应用阈值
cA_denoised = wthresh(cA, threshold, threshold_method);
cH_denoised = wthresh(cH, threshold, threshold_method);
cV_denoised = wthresh(cV, threshold, threshold_method);
cD_denoised = wthresh(cD, threshold, threshold_method);

% 重建图像
img_denoised = idwt2(cA_denoised, cH_denoised, cV_denoised, cD_denoised, wavelet_name);

% 显示降噪后的图像
figure;
imshow(img_denoised);
title('降噪后的图像');

#### 5.1.2 效果展示

使用上述代码对一张噪声图像进行降噪，降噪效果如下：

从对比图中可以看出，小波变换降噪可以有效去除图像中的噪声，同时保留图像的细节。

### 5.2 图像边缘检测实战

#### 5.2.1 代码实现

% 读取图像
img = imread('edge_image.jpg');

% 将图像转换为灰度图
img_gray = rgb2gray(img);

% 选择小波基
wavelet_name = 'db4';

% 分解图像
[cA, cH, cV, cD] = dwt2(img_gray, wavelet_name);

% 提取水平和垂直边缘
edges_horizontal = abs(cH);
edges_vertical = abs(cV);

% 合并水平和垂直边缘
edges = sqrt(edges_horizontal.^2 + edges_vertical.^2);

% 二值化边缘
edges_binary = edges > 0.1;

% 显示边缘检测结果
figure;
imshow(edges_binary);
title('边缘检测结果');

#### 5.2.2 效果展示

使用上述代码对一张图像进行边缘检测，边缘检测效果如下：

从边缘检测结果中可以看出，小波变换边缘检测可以准确地检测出图像中的边缘，并且边缘定位清晰。

# 6. 小波变换在图像处理中的展望

小波变换在图像处理领域取得了显著的成功，并展现出广阔的应用前景。随着技术的不断发展，小波变换在图像处理中的应用将进一步拓展和深化。

### 新型小波基的探索

现有的小波基在处理某些特定图像特征时可能存在局限性。因此，探索和开发新的、更有效的的小波基对于提高图像处理的性能至关重要。例如，双正交小波、紧支集小波和多分辨率分析小波等新型小波基正在受到广泛的研究。

### 深度学习与小波变换的融合

深度学习在图像处理领域取得了突破性的进展。将深度学习技术与小波变换相结合，可以充分发挥各自的优势。例如，利用深度学习算法自动提取图像特征，然后使用小波变换进行降噪或边缘检测，可以显著提高处理效率和准确性。

### 硬件加速的小波变换

小波变换的计算量较大，限制了其在实际应用中的实时性。通过硬件加速技术，例如FPGA和GPU，可以大幅提升小波变换的处理速度。这将使小波变换在实时图像处理、视频处理等领域得到更广泛的应用。

### 云计算与小波变换的结合

云计算平台提供了强大的计算资源和存储空间。将小波变换与云计算相结合，可以实现大规模图像处理任务的并行计算。这将大大缩短图像处理的时间，满足大数据时代的图像处理需求。

### 图像处理领域的创新应用

小波变换在图像处理领域不断涌现出新的创新应用，例如：

- **图像超分辨率重建：**利用小波变换的多尺度分解特性，可以从低分辨率图像重建出高分辨率图像。
- **图像去雾：**小波变换可以有效去除图像中的雾气，提高图像的清晰度。
- **图像分水岭分割：**小波变换可以辅助图像分水岭分割算法，提高分割精度。
- **图像纹理分析：**小波变换可以提取图像的纹理特征，用于图像分类、检索和识别。

### 总结

小波变换在图像处理领域具有广阔的应用前景。随着新型小波基的探索、深度学习的融合、硬件加速的实现、云计算的结合以及创新应用的不断涌现，小波变换将继续在图像处理领域发挥重要作用，为图像处理技术的进步做出贡献。