【atan函数揭秘】：从数学原理到编程实现，全面解析atan函数，让你成为atan大师

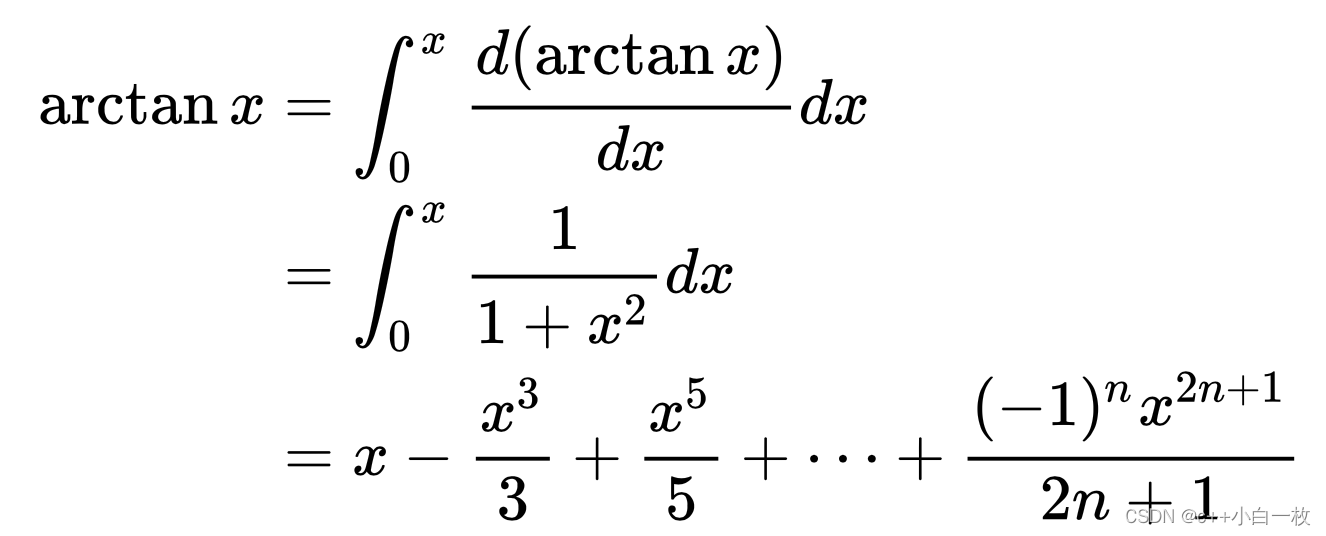
# 1. atan函数的数学原理**

atan函数是反切函数，用于计算给定正切值对应的角度。其数学定义为：

atan(x) = arctan(x) = θ

其中：

* x：正切值
* θ：与x对应的角度（以弧度表示）

atan函数的取值范围为[-π/2, π/2]。当x为正时，θ为正角；当x为负时，θ为负角。

# 2. atan函数的编程实现

### 2.1 atan函数的C语言实现

#### 2.1.1 atan函数的原型和参数

double atan(double x);

| 参数 | 描述 |
|---|---|
| `x` | 输入参数，表示要计算反正切值的数字 |
| 返回值 | 返回反正切值，单位为弧度 |

#### 2.1.2 atan函数的算法原理

C语言中的atan函数使用CORDIC算法来计算反正切值。CORDIC算法是一种迭代算法，它通过一系列旋转操作来逼近反正切值。算法的具体步骤如下：

1. 初始化迭代变量：
- `x0 = x`
- `y0 = 0`
- `z0 = 1`
- `k = 0`

2. 迭代计算：
- 计算当前迭代的反正切值估计：

     atan_est = z0 * atan_table[k]

- 计算当前迭代的旋转角度：

     theta = atan_table[k]

- 根据旋转角度更新迭代变量：

     x0 = x0 * cos(theta) - y0 * sin(theta)
     y0 = y0 * cos(theta) + x0 * sin(theta)
     z0 = z0 * sqrt(1 - atan_table[k]^2)

- 更新迭代次数：

     k = k + 1

3. 迭代结束条件：
- 当迭代次数达到最大迭代次数或精度达到要求时，停止迭代。

4. 返回最终结果：
- 返回计算得到的反正切值估计。

其中，`atan_table`是一个预先计算好的反正切值表，用于提高算法的效率。

### 2.2 atan函数的其他编程语言实现

#### 2.2.1 Python中的atan函数

import math

def atan(x):
  """
  计算反正切值。

  Args:
    x: 输入参数，表示要计算反正切值的数字。

  Returns:
    反正切值，单位为弧度。
  """

  return math.atan(x)

Python中的atan函数使用C语言实现的atan函数，因此算法原理与C语言中的atan函数相同。

#### 2.2.2 Java中的atan函数

import java.lang.Math;

public class AtanFunction {

  public static double atan(double x) {
    """
    计算反正切值。

    Args:
      x: 输入参数，表示要计算反正切值的数字。

    Returns:
      反正切值，单位为弧度。
    """

    return Math.atan(x);
  }
}

Java中的atan函数使用Java虚拟机提供的本地方法实现，因此算法原理与C语言中的atan函数相同。

# 3. atan函数的应用场景

### 3.1 三角函数的计算

atan函数在三角函数的计算中扮演着至关重要的角色。它可以用来计算正切和余切函数的值。

#### 3.1.1 正切函数的计算

正切函数（tan）定义为对边与邻边的比值。使用atan函数，我们可以通过以下公式计算正切函数的值：

double tan(double angle) {
  return sin(angle) / cos(angle);
}

其中，`angle` 是以弧度表示的角度。

#### 3.1.2 余切函数的计算

余切函数（cot）定义为邻边与对边的比值。使用atan函数，我们可以通过以下公式计算余切函数的值：

double cot(double angle) {
  return 1.0 / tan(angle);
}

### 3.2 角度转换

atan函数还广泛用于角度转换，包括弧度与角度的转换以及角度与坡度的转换。

#### 3.2.1 弧度与角度的转换

弧度和角度是测量角度的两种不同单位。弧度以圆周率 π 为单位，而角度以度为单位。使用atan函数，我们可以通过以下公式进行弧度与角度的转换：

double radians_to_degrees(double radians) {
  return radians * (180.0 / M_PI);
}

double degrees_to_radians(double degrees) {
  return degrees * (M_PI / 180.0);
}

#### 3.2.2 角度与坡度的转换

坡度是测量斜率的一种方式，它表示垂直方向上的变化与水平方向上的变化之比。使用atan函数，我们可以通过以下公式进行角度与坡度的转换：

double angle_to_slope(double angle) {
  return tan(angle);
}

double slope_to_angle(double slope) {
  return atan(slope);
}

# 4. atan函数的精度和误差

### 4.1 atan函数的精度分析

#### 4.1.1 浮点数表示的误差

atan函数的精度受限于浮点数表示的误差。浮点数使用二进制小数表示实数，但并不是所有实数都可以精确表示为浮点数。例如，小数0.1无法精确表示为浮点数，因为它的二进制小数表示是无限不循环的。

当atan函数处理浮点数输入时，输入值可能会由于浮点数表示的误差而与实际值略有不同。这会导致atan函数计算出的结果与精确结果之间存在误差。

#### 4.1.2 算法实现的误差

atan函数的算法实现也可能引入误差。atan函数通常使用泰勒级数或查表法进行计算。泰勒级数是一种近似方法，它在某些情况下可能会产生误差。查表法则需要存储大量的预先计算的值，这可能会导致内存开销和性能问题。

### 4.2 atan函数的误差补偿方法

为了减轻atan函数的精度误差，可以采用以下误差补偿方法：

#### 4.2.1 迭代法

迭代法通过迭代地计算atan函数的值来提高精度。在每次迭代中，函数使用前一次迭代的结果作为新的输入值，并计算一个更精确的结果。迭代过程持续进行，直到达到所需的精度。

def atan_iterative(x, n):
    """
    使用迭代法计算atan(x)

    参数：
        x: 输入值
        n: 迭代次数

    返回：
        atan(x)的近似值
    """
    y = 0
    for i in range(n):
        y += x**2 / (2*i + 1)
        x = -x**2 / (2*i + 3)
    return y

#### 4.2.2 分段逼近法

分段逼近法将atan函数的输入范围划分为多个子区间，并在每个子区间内使用不同的近似公式。通过选择合适的近似公式，可以在每个子区间内获得更高的精度。

def atan_piecewise(x):
    """
    使用分段逼近法计算atan(x)

    参数：
        x: 输入值

    返回：
        atan(x)的近似值
    """
    if abs(x) <= 0.5:
        return x - x**3 / 3 + x**5 / 5
    elif abs(x) <= 1:
        return pi / 2 - atan(1 / x)
    else:
        return pi - atan(1 / x)

# 5. atan函数的优化技巧**

### 5.1 atan函数的性能优化

**5.1.1 使用近似算法**

对于某些特定输入范围，我们可以使用近似算法来近似计算atan函数的值，从而提高性能。例如，对于输入值接近0时，我们可以使用以下近似公式：

atan(x) ≈ x - x^3/3 + x^5/5 - x^7/7

**5.1.2 利用硬件加速**

现代CPU通常提供硬件加速指令来计算三角函数，包括atan函数。这些指令可以显著提高atan函数的计算速度。例如，x86 CPU提供`atan2`指令，它可以同时计算atan函数和atan2函数的值。

### 5.2 atan函数的内存优化

**5.2.1 减少中间变量的分配**

atan函数的计算通常需要分配多个中间变量。为了减少内存开销，我们可以通过重用变量或使用局部变量来减少中间变量的分配。

**5.2.2 使用内存池**

对于需要频繁分配和释放内存的应用，我们可以使用内存池来管理内存分配。内存池可以预先分配一块内存，并在需要时从中分配和释放内存块，从而减少内存碎片化和提高内存分配效率。