【统计学视角下的PCA】：方差解释与累积贡献率深入理解

# 1. 主成分分析（PCA）的基本概念

在当今数据驱动的世界中，数据集的维度往往极高，这对存储、计算以及数据解释提出了巨大的挑战。主成分分析（PCA）作为一种经典的降维技术，通过线性变换将数据集映射到低维度空间，同时保留了数据的最重要特征。本章旨在为你揭示PCA的基本概念，为深入理解后续章节中的数学原理和应用奠定基础。

PCA的核心在于寻找数据的内在结构，通过这种转换，可使得数据在新的坐标系下的方差达到最大。它不仅减少了数据的复杂度，而且还帮助我们识别出影响数据集的主要因素。对于IT专业人员，尤其是数据分析师和数据科学家来说，掌握PCA是解读数据、提取洞见不可或缺的工具。接下来，我们会探讨PCA如何实现这一目标，并解释为何它在数据挖掘和模式识别中占据重要地位。

# 2. PCA的数学基础与理论框架

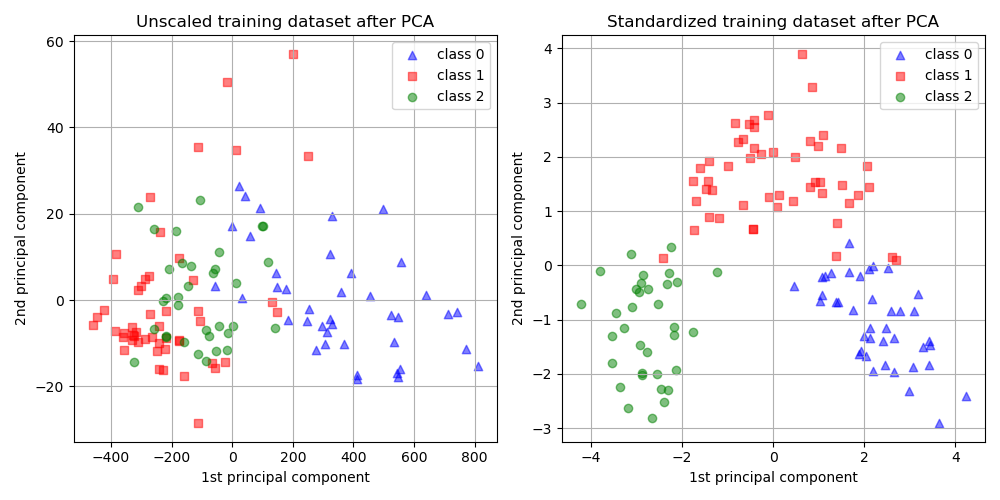
### 2.1 向量空间与特征分解
#### 2.1.1 向量空间的定义和性质
向量空间（也称为线性空间）是线性代数中的一个核心概念，它是由向量构成的一个集合，满足以下性质：

1. **封闭性**：空间内的任意两个向量相加，结果仍然在该空间内。
2. **加法和数乘运算**：空间内的向量可以进行加法运算和数乘运算，并且这两种运算满足八条基本规则（如结合律、交换律等）。
3. **零向量存在性**：空间内存在一个零向量，使得任意向量加零向量等于自身。
4. **负向量存在性**：对于空间内的任意向量，都存在一个对应的负向量，使得两个向量相加等于零向量。
5. **线性无关**：如果一组向量的线性组合仅有一个解（即所有系数为零），那么这组向量线性无关。

这些性质使得向量空间成为了一种富有结构且可以进行复杂操作的数学对象。在PCA中，数据集可以被视为多维空间中的点集，而向量空间的概念则帮助我们理解数据的分布和结构。

#### 2.1.2 特征值和特征向量的概念
在PCA的数学框架中，特征值（eigenvalues）和特征向量（eigenvectors）扮演着关键的角色。考虑一个方阵\( A \)，如果存在一个非零向量\( \mathbf{v} \)和一个标量\( \lambda \)，使得下列等式成立：

\[ A\mathbf{v} = \lambda\mathbf{v} \]

那么\( \mathbf{v} \)被称为\( A \)的一个特征向量，而对应的\( \lambda \)被称为特征值。特征向量代表了方阵\( A \)在变换下保持方向不变的向量，而特征值表示了变换后向量长度的缩放因子。

在PCA中，数据协方差矩阵的特征值和特征向量尤其重要，它们直接关联到主成分的提取。主成分是特征向量，而特征值则代表了每个主成分所解释的数据方差量，是选择主成分时的关键参考。

#### 2.1.3 矩阵的特征分解过程
特征分解（也称为谱分解）是线性代数中的一种分解方法，它将一个方阵分解为一系列的特征向量和特征值。对于一个\( n \times n \)的方阵\( A \)，特征分解的过程可描述为：

\[ A = Q\Lambda Q^{-1} \]

其中，\( Q \)是由\( A \)的所有特征向量构成的矩阵，而\( \Lambda \)是一个对角矩阵，其对角线上的元素是\( A \)的特征值。特征分解的一个重要应用是在数据降维中，它可以被用来将原始数据投影到由特征向量张成的低维空间上。

### 2.2 PCA的优化目标和数学表达
#### 2.2.1 数据降维的目标函数
PCA作为一种数据降维方法，它的目标函数是最大化投影后的数据方差。PCA的优化目标可以表述为：

\[ \max_{\mathbf{w}_1} \text{Var}\left(\mathbf{w}_1^T \mathbf{x}\right) \]

其中，\( \mathbf{w}_1 \)是第一个主成分，\( \mathbf{x} \)是原始数据向量。目标函数要求在第一个主成分方向上，投影后的数据具有最大的方差。

#### 2.2.2 最大化方差的统计意义
数据的方差代表了数据点在主成分方向上的分散程度。最大化方差的统计意义在于确保所选取的主成分能够尽可能地捕捉数据的变异性。在降维的过程中，我们希望降维后的数据能够保留原始数据的重要信息。通过最大化投影数据的方差，PCA可以保留最有意义的数据变化特征。

#### 2.2.3 主成分的选择标准
在PCA中，主成分的选择基于特征值的大小。由于特征值代表了对应特征向量方向上的数据方差，所以特征值越大，相应的特征向量就越重要。主成分的选择标准是按照特征值从大到小排序，并选取前\( k \)个最大的特征值对应的特征向量作为主成分。这里的\( k \)通常是根据累计贡献率来确定的。

### 2.3 方差解释与累计贡献率的理论基础
#### 2.3.1 方差解释的定义及其重要性
方差解释是指在PCA中，某个主成分所解释的数据方差的百分比。它是衡量该主成分重要性的一个指标。每个主成分的方差解释可以通过其对应的特征值与总特征值之和的比例来计算。

方差解释的重要性在于它直接关联到数据降维的效果。如果一个主成分解释了较高的方差，说明它捕捉到了数据中的主要变化趋势，因此该主成分在降维中是关键的。

#### 2.3.2 累计贡献率的概念及其计算方法
累计贡献率是指前\( k \)个主成分解释的方差占总方差的比例。累计贡献率可以通过以下公式计算：

\[ \text{累计贡献率} = \frac{\sum_{i=1}^{k} \lambda_i}{\sum_{j=1}^{n} \lambda_j} \]

其中，\( \lambda_i \)是按降序排列的特征值，\( n \)是总特征值的数量。累计贡献率用于评估选定的\( k \)个主成分对原始数据总方差的解释能力。

#### 2.3.3 累计贡献率与数据降维的关系
在PCA中，选择主成分的数量\( k \)是降维过程中的一个关键决策。累计贡献率为我们提供了一个客观的衡量标准。一般来说，选择一个使得累计贡献率达到一定阈值（如90%或95%）的\( k \)值，可以认为我们保留了原始数据的大部分信息。

累计贡献率与数据降维之间的关系体现了在信息损失与计算效率之间的权衡。通过累计贡献率，我们可以量化地评估信息损失的程度，并据此做出是否接受某个降维方案的决策。

在接下来的章节中，我们将深入探讨PCA的统计学解释及其在实际应用中的具体步骤和策略。

# 3. PCA的统计学解释

## 3.1 方差与数据分散性的度量

### 3.1.1 方差作为数据分散性的指标

方差是统计学中衡量一组数值分散程度的度量。在PCA中，方差与主成分的抽取有直接关系，因为PCA的核心思想是通过正交变换将一组可能相关的变量转换为一组线性不相关的变量，这些新变量称为主成分。第一个主成分解释了数据中最多的方差，第二个主成分解释了剩余数据中方差的最大部分，依此类推。

方差的计算公式是：

\[ \sigma^2 = \frac{\sum_{i=1}^{n}(x_i - \mu)^2}{n} \]

其中，\(x_i\) 表示数据集中第 \(i\) 个样本值，\(\mu\) 表示样本均值，\(n\) 是样本总数。在PCA的背景下，方差可以视为一个衡量数据点与数据集中心点（均值）距离的指标。

方差越大，表示数据点分布得越分散，反之则越集中。在PCA中，由于方差越大意味着包含的信息越多，因此，最大化方差成为PCA中选择主成分的一个重要目标。

### 3.1.2 方差解释在统计学中的角色

方差解释是PCA中一个核心概念，它描述了某个主成分所解释的方差占总体方差的百分比。这个解释度告诉我们在数据降维过程中，每个主成分保留了多少原始数据的变异信息。例如，如果第一个主成分解释了数据总方差的40%，那么我们可以说这个主成分捕获了原始数据集40%的信息。

方差解释的重要性在于，它允许我们量化每个主成分的贡献，并决定在多大程度上可以减少数据集的维度而不会丢失太多信息。在实践中，研究者会计算累计方差解释率，该值是前几个主成分方差解释率的总和，这有助于确定保留多少主成分是合适的。

例如，如果前两个主成分的累计方差解释率达到80%，则可能表明可以用这两个主成分来替代原始的多维数据，而不失去太多信息。

## 3.2 主成分的统计学含义

### 3.2.1 主成分作为数据投影的