【PCA进阶技巧】：避免常见陷阱，数据标准化的重要性

# 1. PCA的基本概念和原理

在现代数据分析中，主成分分析（PCA）是一种常用的数据降维技术，目的是在尽可能保留原有数据信息的前提下，减少数据集的复杂度。PCA通过正交变换将一组可能相关的变量转换成一组线性不相关的变量，这组新变量被称为主成分。在数学上，这些主成分对应于原始数据矩阵的协方差矩阵或相关矩阵的特征值和特征向量。

## 1.1PCA的工作原理

PCA依据特征值分解协方差矩阵，计算出数据的主成分，并将特征值按大小顺序排列。最大的特征值对应的特征向量定义了数据方差最大的方向，称为第一主成分，其后的主成分依次定义了剩余最大方差的方向。通过选择前几个主成分，可以将数据集降维，同时尽可能保留数据的原始特征。

## 1.2 PCA的数学表达

PCA的过程可以用矩阵分解的形式来表示，具体为将数据矩阵X分解为载荷矩阵P和主成分矩阵T的乘积，再加上误差矩阵E。数学表达为X = TP^T + E。这里的P包含了原数据变换到主成分空间的基向量，而T则代表了数据在新空间的坐标。

在应用PCA之前，数据通常需要经过预处理，比如数据标准化，以确保PCA的结果更准确。接下来的章节将深入探讨数据标准化及其对PCA的影响。

# 2. 数据标准化的核心作用

## 2.1 数据标准化的目的和意义
### 2.1.1 数据分布和方差对PCA的影响

主成分分析（PCA）是一种统计方法，它通过正交变换将一组可能相关的变量转换为一组线性不相关的变量，这些新变量称为主成分。在数据集中，变量的方差大小直接影响着PCA的结果。方差大的变量将对主成分有更大的影响，这可能会导致PCA分析结果不准确，尤其当不同变量的量纲和数量级相差悬殊时。

以医疗数据分析为例，某患者的身高和体重可能分别为180厘米和80千克，而血糖值为5.5mmol/L。这三个变量的量纲不同，直接使用PCA分析可能导致身高和体重主导了大部分的方差解释，从而掩盖了血糖值等重要信息的影响。

### 2.1.2 标准化方法选择的影响因素

不同的标准化方法对PCA结果的影响也是显著的。选择最合适的标准化方法需要考虑到数据集的特性，例如数据的分布形态、是否存在离群点以及是否需要特定的数据范围等。

例如，对于含有离群点的数据集，Z-score标准化通常会比最小-最大标准化更加合适。因为Z-score方法是通过减去均值然后除以标准差来计算，对离群点不敏感。而最小-最大标准化则对离群点更为敏感，因为它们会拉大其他数据值的范围。

## 2.2 数据标准化的常用技术

### 2.2.1 Z-score标准化

Z-score标准化是通过减去数据的均值并除以标准差来实现数据的标准化。这种方法使得数据具有0均值和单位方差。

from sklearn.preprocessing import StandardScaler
import numpy as np

# 假设X原始数据集
X = np.array([[1, 2], [3, 4], [5, 6]])

# Z-score标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

print(X_scaled)

以上代码将输入数据X进行Z-score标准化，每个特征的均值会变为0，标准差变为1。这样处理后，数据集将更加适合进行后续的PCA分析。

### 2.2.2 最小-最大标准化

最小-最大标准化是将每个特征缩放到一个指定的范围，通常是[0, 1]。这通过最小值和最大值将每个特征缩放进行标准化。

from sklearn.preprocessing import MinMaxScaler

# 假设X原始数据集
X = np.array([[1, 2], [3, 4], [5, 6]])

# 最小-最大标准化
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

print(X_scaled)

这段代码将数据集X的每个特征的值缩放到[0, 1]区间内。需要注意的是，最小-最大标准化对于离群值非常敏感，因此在存在异常值的情况下可能不是最佳选择。

### 2.2.3 归一化

归一化通常指的是将数据缩放到特定的范围，例如[0, 1]。这个过程与最小-最大标准化相似，但归一化有时也特指将数据的总和变为1。

在PCA中，我们通常关注的是将数据变换到具有单位方差的形式，所以归一化不常用于PCA的前处理，除非目的是将数据集中到特定区间。

## 2.3 数据标准化在PCA中的实践

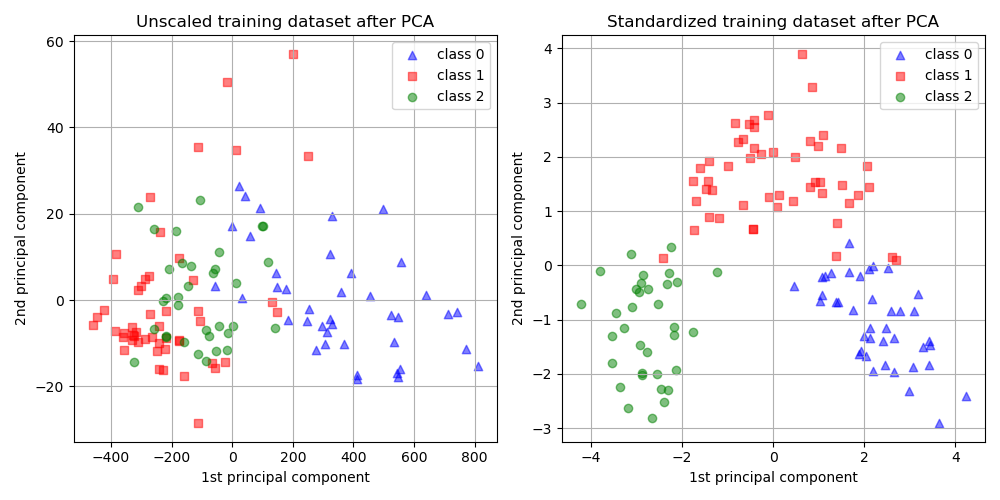
### 2.3.1 标准化前后数据的对比分析

标准化处理前后，数据的分布会有明显的区别。未标准化的数据可能存在量纲的不一致和量级的差别，使得PCA的计算结果受到数据集中特定变量的方差影响较大。标准化后，数据具有统一的量纲和量级，能够更加公平地反映各变量在数据集中的作用。

### 2.3.2 标准化对主成分分析结果的影响

标准化处理可以显著影响PCA的结果。例如，在未标准化的情况下，方差大的变量可能主导了PCA分析，而在标准化之后，由于每个变量都具有相同的方差，PCA分析会更加准确地反映数据结构。

下面是一个对比标准化前后进行PCA分析的案例：

from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 假设X原始数据集和X标准化后的数据集
X = np.array([[1, 2], [3, 4], [5, 6]])
X_scaled = StandardScaler().fit_transform(X)

# 未标准化的PCA分析
pca = PCA()
pca.fit(X)
# 标准化后的PCA分析
pca_scaled = PCA()
pca_scaled.fit(X_scaled)

# 绘制主成分解释的方差比例图
plt.figure(figsize=(14, 5))
plt.subplot(1, 2, 1)
plt.bar(range(1, 3), pca.explained_variance_ratio_)
plt.title('未标准化数据的PCA')
plt.ylabel('方差比例')

plt.subplot(1, 2, 2)
plt.bar(range(1, 3), pca_scaled.explained_variance_ratio_)
plt.title('标准化数据的PCA')
plt.ylabel('方差比例')

plt.tight_layout()
plt.show()

上述代码将展示未标准化与标准化数据在PCA分析后，主成分解释的方差比例的区别。可以看到，标准化处理后的数据能够更均衡地展现每个变量的方差贡献。

# 3. 避免PCA的常见陷阱

## 3.1 数据相关性分析

### 3.1.1 多重共线性问题

在进行主成分分析（PCA）之前，数据集中的变量可能存在多重共线性问题，这指的是多个变量之间存在较高的线性相关性。多重共线性会导致PCA中的特征值分解出现不稳定性，进而影响主成分的选择和解释。

多重共线性问题常见于：

- 经济学和社会科学的数据，其中可能包含相互关联的社会、经济指标。
- 生物统计学中，基因表达数据的多个基因间可能有共同的调控机制。
- 工程领域中，某些物理参数间存在自然的相互依赖关系。

在实际操作中，可以采用以下方法识别并处理多重共线性问题：

1. 观察相关性矩阵（Correlation Matrix），确认变量间是否存在高相关系数（通常>0.9）。
2. 使用方差膨胀因子（Variance Inflation Factor, VIF），VIF值大于10时可能表明存在多重共线性。
3. 应用主成分分析之前进行特征选择，只保留与目标变量有较强关系的特征。
4. 采用偏最小二乘回归（Partial Least Squares, PLS）等其他技术替代PCA。

### 3.1.2 特征选择的影响

特征选择是影响PCA结果的重要因素之一。通过选择哪些特征来代表数据集，可以显著地影响主成分的构成和解释。

在特征选择过程中，应当考虑：

- 变量的信息量：信息量大的变量可能更值得保留。
- 变量的代表性和解释性：某些变量可能更能代表数据集中的重要信息。
- 变量间的关系：避免选择高度相关的特征，以减少多重共线性的影响。

在特征选择时可使用以下方法：

- 筛选法（Filter Methods）：如基于统计测试的特征选择，包括卡方检验、ANOVA等。
- 包裹法（Wrapper Methods）：如递归特征消除（Recursive Feature Elimination, RFE）。
- 嵌入法（Embedded Methods）：如基于LASSO和岭回归的特征选择。

## 3.2 主成分的解释和选择

### 3.2.1 累计贡献率的误导

在PCA中，主成分按照其解释的方差的大小进行排序。通常人们会关注前几个主成分，认为它们解释了大部分的数据方差，并使用这些主成分作为数据的降维表示。

但是，累计贡献率可能会有误导性。如果前几个主成分解释的方差累计贡献率达到一个看似很高的百分比（比如85%），这可能并不意味着其他主成分不重要。在某些情况下，剩余的主成分可能解释了数据中一些独特的、重要的结构信息。

为了避免被累计贡献率误导，可以采取以下措施：

- 仔细分析每一个主成分的特征值和特征向量，以理解它们具体解释了哪些数据特征。
- 查看碎石图（Scree Plot）来直观地判断主成分的重要程度。
- 在模型选择时考虑业务需求，如果需要对数据做更深入的分析，可能需要保留更多的主成分。

### 3.2.2 特征值与特征向量的解读

在PCA中，特征值和特征向量是核心元素。特征值代表了对应主成分解释数据方差的能力，而特征向量则定义了数据降维后新空间的方向。

理解特征值和特征向量的步骤包括：

- **分析特征值**：较大的特征值表明对应主成分能够解释较多的数据方差。
- **解释特征向量**：特征向量向量指示原始数据空间中哪些方向最重要，即它们是新特征轴的系数。
- **使用图形工具**：例如，绘制特征向量的散点图可以直观地展示数据的分布趋势。

为了更好地解释特征值和特征向量，通常需要执行以下操作：

- 对特征值进行排序，并与各主成分关联。
- 对特征向量进行可视化，使用散点图、热图等方法。
- 结合业务知识进行解释，将数学结果转化为领域内的实际含义。

## 3.3 超参数选择与模型验证

### 3.3.1 保留主成分的数量选择

选择保留多少个主成分是PCA中的一个关键超参数。保留太少可能会丢失重要的数据信息，而保留太多可能会引入不必要的噪声。

常用的方法有：

- **累计贡献率