【PCA算法构建】：从概念到实现的逐步指导

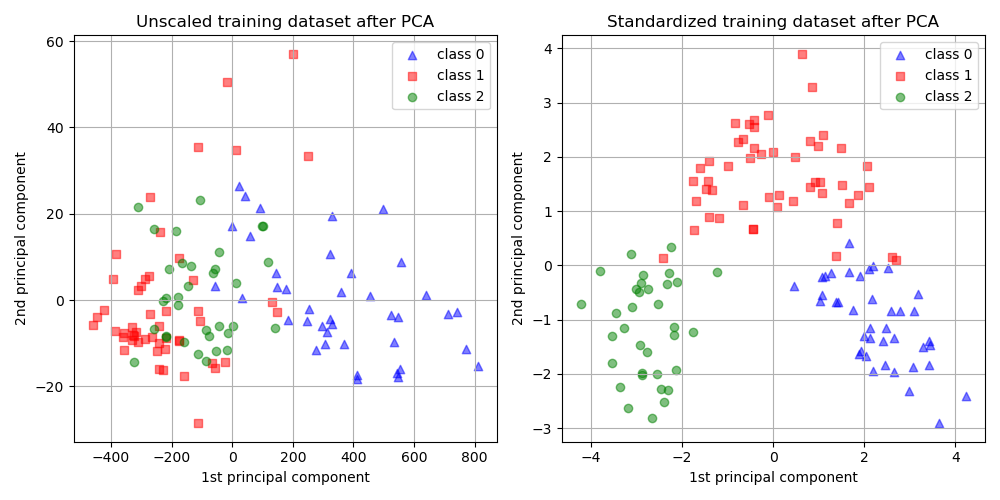
# 1. PCA算法概述与数学基础

在现代数据科学中，主成分分析（PCA）是降维技术的基石之一，它通过数学变换来减少数据集的复杂度，同时尽可能保留原始数据的重要特征。PCA在图像处理、生物信息学、金融分析等领域拥有广泛的应用。

## 1.1 PCA算法的定义和目的

PCA旨在通过正交变换，将一组可能相关的变量转换为一组线性不相关的变量，这些新变量称为主成分。其主要目的是数据降维，提高数据处理的效率，同时保留数据的关键信息。

## 1.2 PCA算法的工作原理

PCA基于数据的协方差矩阵，找到方差最大的方向，将数据投影到这些方向上，形成新的特征空间。每个主成分都是原始数据在这些方向上的投影，并按方差大小排序，方差越大代表包含的信息越多。

## 1.3 PCA算法的数学基础

为了深入理解PCA，需要掌握线性代数中的一些基础知识，如矩阵运算、特征值和特征向量等。这些数学工具是PCA算法实现的核心。

设X是n维随机向量，PCA的目的是找到一个线性变换W，将X映射到低维空间的向量Y，即Y = W^T * X，其中W是由数据的协方差矩阵的特征向量组成的矩阵。

在本章节中，我们将介绍PCA的数学基础，并逐步搭建起理解整个PCA算法的知识框架。

# 2. 理解PCA算法的理论框架

## 2.1 主成分分析的数学原理

### 2.1.1 数据的协方差矩阵

在多变量统计分析中，协方差矩阵是用来表示数据特征之间相互关系的重要工具。在主成分分析（PCA）中，协方差矩阵是推导主成分的基础。设有数据集 \(X\)，其中每个观测向量有 \(p\) 个变量，数据矩阵 \(X\) 的大小为 \(n \times p\)（\(n\) 为观测数，\(p\) 为变量数）。数据集 \(X\) 中心化处理（即减去均值）后，可以得到其协方差矩阵 \(C\)，该矩阵的元素由下式给出：

\[ C = \frac{1}{n-1} X^T X \]

其中，\(X^T\) 是 \(X\) 的转置矩阵，\(X^T X\) 是样本协方差矩阵的运算表达。

协方差矩阵的每个元素表示两个变量之间的协方差，它描述了它们共同变化的趋势。如果两个变量之间正相关，协方差为正值；如果负相关，则为负值；如果独立，则为零。协方差矩阵的对角线元素则为每个变量的方差，表示变量波动的程度。

在实现PCA时，通过求解协方差矩阵的特征值和特征向量，可以获得数据最重要的变化方向，从而实现数据的降维。

### 2.1.2 特征值和特征向量的角色

特征值和特征向量在PCA算法中扮演了核心角色。对于协方差矩阵 \(C\)，其特征值和特征向量的计算通常通过特征分解来完成，即求解方程：

\[ C \mathbf{v} = \lambda \mathbf{v} \]

这里 \(\mathbf{v}\) 是特征向量，而 \(\lambda\) 是对应的特征值。特征值表示了在对应特征向量方向上的方差大小，特征值越大，该方向的数据变异性越大，即该方向越重要。在PCA中，我们通常按照特征值从大到小的顺序来排列特征向量。

通过选择最大的 \(k\) 个特征值及其对应的特征向量，我们可以构造一个投影矩阵 \(P\)：

\[ P = \begin{bmatrix} | & | & & | \\ \mathbf{v}_1 & \mathbf{v}_2 & \dots & \mathbf{v}_k \\ | & | & & | \end{bmatrix} \]

将原始数据 \(X\) 投影到由这些特征向量构成的新空间中，我们可以得到降维后的数据。

## 2.2 降维的统计意义

### 2.2.1 方差最大化与信息保留

在数据降维的过程中，目标是尽可能保留原始数据的重要信息，同时去除冗余和噪声。PCA通过最大化保留数据的方差来实现这一点。在PCA中，我们假设数据的大部分信息都包含在方差最大的方向上，因为方差大的方向反映了数据的最大波动和信息。

因此，在PCA中，选择特征向量的过程实际上是在选择一个正交的方向，这些方向依次对应于协方差矩阵中最大的特征值。每个选择的特征向量都会保留一个最大方差的方向，所以第一个主成分拥有最大的方差，第二个次之，以此类推。通过组合这些主成分，我们可以重构原始数据，并且在每个方向上保留尽可能多的信息。

### 2.2.2 如何选择主成分的数量

选择主成分的数量是PCA应用中的一个重要决策。这个决策过程通常基于两个主要考虑：方差的解释度和累计方差的百分比。

首先，通过分析协方差矩阵的特征值，可以确定每个主成分解释的方差量。然后，计算累计方差的百分比，即前 \(k\) 个主成分解释的方差总和占总方差的比例。一般目标是选择尽可能少的主成分，同时确保这些主成分可以保留原始数据的大部分信息。通常，累计百分比达到80%或90%即可认为是满意的结果，但具体阈值还需视实际问题而定。

在实际操作中，可以绘制一个“累计方差解释图”，该图横坐标表示主成分的数量，纵坐标表示累计方差百分比。通过观察图中曲线的斜率变化，选择一个“拐点”，即增加一个主成分导致累计方差的增加显著减少的点。这个点之后的主成分可认为是冗余的，可以被舍弃。

## 2.3 PCA的几何解释

### 2.3.1 数据变换的几何直观

PCA的几何解释可以帮助我们更直观地理解数据在降维后的变化。在多维空间中，每一个数据点可以被视为一个向量，而PCA的主要思想是找到一个低维空间，将这些向量投影到这个空间上，从而达到降维的目的。

从几何角度看，PCA选择的每一个主成分都可以看作是原始数据空间的一个轴，而这些轴都是正交的。通过这些轴，我们可以重新定义一个新的坐标系，它反映了数据分布的方向性。数据在新坐标系中的坐标即为降维后的数据。

第一个主成分指向数据分布中最大方差的方向，它捕捉了数据变化的最大部分。随后的每个主成分都与前一个正交，并指向方差次大的方向，以此类推，直到覆盖了数据的主要变化。通过这种方式，PCA在减少数据维度的同时，尽可能保留了原始数据的结构特征。

### 2.3.2 数据压缩的几何效果

通过PCA降维后，数据不仅在数量上减少，而且其几何结构也发生了变化。数据压缩的几何效果通常体现在两个方面：数据点分布的简化和数据变化方向的捕捉。

当数据降维到较低的维度时，原来在高维空间中可能呈现出复杂结构的数据点，现在在低维空间中可能仅展示为一组点云。这个点云会尽可能保持原始数据的分布特征，但细节可能会丢失。例如，高维空间中可能存在的聚类现象，在低维空间中可能表现为紧密的群集，但无法精确展现原始聚类的形状和边界。

此外，数据变化的主要方向将被主成分捕捉，并在新的坐标轴上表现出来。这些新的坐标轴对应于数据的方差大小，即主成分的特征值大小。选择较大的特征值对应的主成分，可以捕捉到数据的主要变化，而忽略那些方差小、变化不显著的方向。

在实际应用中，选择合适的主成分数量是至关重要的。通常需要权衡降维带来的信息损失与模型简化带来的收益。例如，在机器学习模型中，过多的特征可能会导致模型过拟合，而PCA降维则有助于简化模型，提高泛化能力。

以下是使用Python中的NumPy库进行PCA的几何解释的示例代码：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 假设data是一个3D数据集
data = np.random.randn(100, 3)

# 计算数据的协方差矩阵
cov_matrix = np.cov(data, rowvar=False)

# 求解特征值和特征向量
eigen_values, eigen_vectors = np.linalg.eig(cov_matrix)

# 选择最大的三个特征值及其特征向量
sorted_indices = np.argsort(eigen_values)[::-1]
top_eigen_vectors = eigen_vectors[:, sorted_indices[:3]]

# 创建3D图
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[:, 0], data[:, 1], data[:, 2], c='r', marker='o')

# 在新的坐标系中绘制数据点
data_transformed = np.dot(top_eigen_vectors.transpose(), (data - np.mean(data, axis=0)).T).T
ax.scatter(data_transformed[:, 0],