分析MATLAB散点图错误：避免数据可视化陷阱，确保数据准确性

# 1. MATLAB散点图简介**

散点图是一种常用的数据可视化工具，用于显示两个变量之间的关系。在MATLAB中，可以使用`scatter`函数创建散点图。

散点图由一组点组成，每个点代表一个数据点。点的水平位置由第一个变量的值确定，而垂直位置由第二个变量的值确定。通过观察点的分布，可以了解变量之间的关系，例如相关性、趋势或异常值。

# 2. 散点图错误的理论基础

散点图是一种广泛使用的可视化工具，用于探索数据之间的关系。然而，如果没有正确的理论基础，散点图可能会产生误导性的结果。本章节将探讨散点图的三个常见错误理论基础：数据分布和异常值、相关性和因果关系，以及偏见和混淆变量。

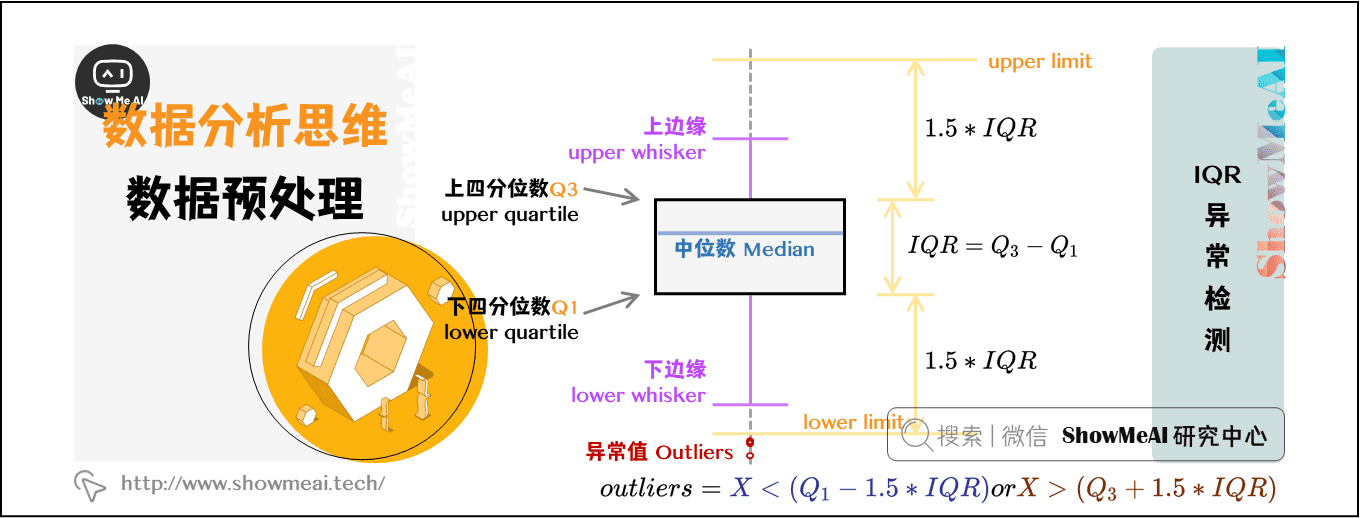
### 2.1 数据分布和异常值

**数据分布**

数据分布描述了数据点的分布情况。散点图中，数据点通常沿x轴和y轴分布。数据分布可以是正态分布、偏态分布或均匀分布。

**异常值**

异常值是与其他数据点明显不同的数据点。它们可以是极端值、缺失值或错误值。异常值会扭曲散点图的形状和趋势，从而导致误导性的结论。

**错误基础：**

* 假设数据呈正态分布，而实际上可能是偏态分布或均匀分布。
* 忽略异常值，从而低估或高估数据之间的关系。

### 2.2 相关性和因果关系

**相关性**

相关性衡量两个变量之间线性关系的强度。相关系数在-1到1之间，其中-1表示完全负相关，0表示无相关，1表示完全正相关。

**因果关系**

因果关系是指一个变量的变化导致另一个变量的变化。

**错误基础：**

* 将相关性误认为因果关系。相关性并不一定意味着因果关系。
* 忽略潜在的混淆变量，这些变量会影响两个变量之间的关系。

### 2.3 偏见和混淆变量

**偏见**

偏见是指由于数据收集或分析过程中的系统性错误而导致的估计值不准确。

**混淆变量**

混淆变量是影响两个变量之间关系的第三方变量。它们会产生偏见，从而导致误导性的结论。

**错误基础：**

* 忽略偏见，从而导致估计值不准确。
* 未控制混淆变量，从而导致错误地解释两个变量之间的关系。

**代码示例：**

% 生成包含异常值的数据
data = [randn(100, 1); 100 * randn(1, 1)];

% 创建散点图
scatter(data, data);
xlabel('X');
ylabel('Y');

% 分析异常值的影响
outliers = find(abs(data) > 3);
scatter(data(outliers), data(outliers), 'ro');
legend('Normal data', 'Outliers');

**代码逻辑分析：**

* 第1行：生成包含异常值的数据，其中正态分布数据和异常值分别用不同的颜色表示。
* 第4-6行：创建散点图，显示正常数据和异常值。
* 第8-10行：找出异常值，并用红色圆圈表示。
* 第11行：添加图例，区分正常数据和异常值。

**参数说明：**

* `randn(100, 1)`：生成100个正态分布的随机数。
* `100 * randn(1, 1)`：生成一个异常值，其值为正态分布随机数的100倍。
* `scatter(data, data)`：创建散点图，其中x轴和y轴都使用`data`中的值。
* `xlabel('X')`：设置x轴标签为"X"。
* `ylabel('Y')`：设置y轴标签为"Y"。
* `find(abs(data) > 3)`：找出绝对值大于3的数据点，表示异常值。
* `scatter(data(outliers), data(outliers), 'ro')`：创建散点图，显示异常值，并使用红色圆圈表示。
* `legend('Normal data', 'Outliers')`：添加图例，分别标记正常数据和异常值。

# 3. 避免散点图错误的实践指南

### 3.1 数据准备和预处理

在创建散点图之前，对数据进行适当的准备和预处理至关重要。这包括以下步