时间序列预测模型的优化技巧：提升预测精度的10大秘诀

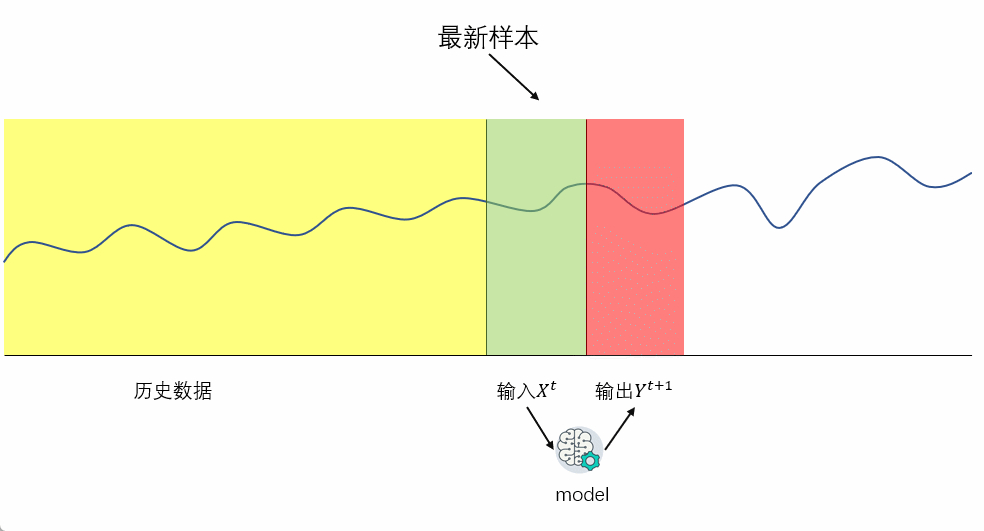
# 1. 时间序列预测模型简介**

时间序列预测模型是一种强大的工具，用于预测未来事件，基于过去和当前数据。这些模型广泛应用于各种领域，如金融、医疗保健、制造业和供应链管理。

时间序列数据具有时序性，这意味着数据点按时间顺序排列。预测模型利用这种时序性来识别模式和趋势，从而对未来的值进行预测。常见的时间序列预测模型包括：

* **ARIMA（自回归综合移动平均）：**一种经典的线性模型，用于预测平稳的时间序列。
* **SARIMA（季节性自回归综合移动平均）：**一种扩展的 ARIMA 模型，用于预测具有季节性模式的时间序列。
* **LSTM（长短期记忆）：**一种神经网络模型，擅长处理复杂的时间序列数据，具有记忆能力。

# 2. 时间序列预测模型的理论基础**

**2.1 时间序列的特征和分解**

时间序列是指按时间顺序排列的一系列数据点。其主要特征包括：

- **趋势性：**数据随时间呈单调上升或下降趋势。
- **季节性：**数据在特定时间间隔内重复出现周期性波动。
- **随机性：**数据中存在不可预测的波动，通常由噪声或其他外部因素引起。

时间序列分解将原始序列分解为趋势、季节性和随机性分量。这有助于理解数据模式并选择合适的预测模型。

**2.2 常见的预测模型：ARIMA、SARIMA、LSTM**

**2.2.1 ARIMA模型**

ARIMA（自回归滑动平均）模型是一种经典的时间序列预测模型。它假设数据遵循自回归和滑动平均过程，即：

Y_t = c + ϕ_1 Y_{t-1} + ϕ_2 Y_{t-2} + ... + ϕ_p Y_{t-p} + θ_1 ε_{t-1} + θ_2 ε_{t-2} + ... + θ_q ε_{t-q}

其中：

- Y_t：预测值
- c：常数项
- ϕ_i：自回归系数
- θ_i：滑动平均系数
- ε_t：白噪声误差项

**2.2.2 SARIMA模型**

SARIMA（季节性ARIMA）模型是ARIMA模型的扩展，考虑了季节性因素。它引入额外的季节性自回归和滑动平均系数，如下所示：

Y_t = c + ϕ_1 Y_{t-1} + ϕ_2 Y_{t-2} + ... + ϕ_p Y_{t-p} + θ_1 ε_{t-1} + θ_2 ε_{t-2} + ... + θ_q ε_{t-q} + S_1 Y_{t-s} + S_2 Y_{t-2s} + ... + S_m Y_{t-ms}

其中：

- s：季节性周期
- S_i：季节性自回归系数

**2.2.3 LSTM模型**

LSTM（长短期记忆）模型是一种神经网络，专门用于处理序列数据。它具有记忆单元，可以学习长期依赖关系。LSTM模型的结构如下：

h_t = f(W_f [h_{t-1}, x_t] + b_f)
c_t = f(W_c [h_{t-1}, x_t] + b_c)
o_t = f(W_o [h_{t-1}, x_t] + b_o)
y_t = o_t * tanh(c_t)

其中：

- h_t：隐藏状态
- c_t：记忆单元
- o_t：输出门
- y_t：输出值
- W_f、W_c、W_o：权重矩阵
- b_f、b_c、b_o：偏置向量
- f：激活函数

# 3.1 数据预处理和特征工程

**数据预处理**

数据预处理是时间序列预测模型构建的关键步骤，其目的是消除数据中的噪声和异常值，并将其转换为适合建模的格式。常见的数据预处理技术包括：

- **缺失值处理：**使用插值或平均值填充缺失值。
- **异常值检测：**识别并删除异常值，避免其对模型造成偏差。
- **数据归一化：**将数据缩放到统一的范围，以提高模型的鲁棒性。
- **平稳化：**通过差分或对数变换等方法，使数据序列平稳，消除趋势或季节性。

**特征工程**

特征工程涉及创建和选择用于预测模型的特征。对于时间序列数据，常用的特征包括：

- **滞后特征：**序列中过去时间点的值。
- **趋势特征：**数据序列的整体趋势，可以通过移动平均或指数平滑等方法提取。
- **季节性特征：**数据序列中周期性的模式，可以通过傅里叶变换或季节性分解等方法提取。
- **外部特征：**与时间序列相关的其他相关信息，例如天气、经济指标等。

### 3.2 模型选择和参数优化

**模型选择**

根据时间序列数据的特征和预测目标，选择合适的预测模型至关重要。常见的时间序列预测模型包括：

- **ARIMA（自回归综合移动平均）：**适用于平稳时间序列，具有自回归、差分和移动平均项。
- **SARIMA（季节性ARIMA）：**适用于具有季节性模式的时间序列。
- **LSTM（长短期记忆）：**一种深度学习模型，擅长处理非线性时间序列数据。

**参数优化**

每个预测模型都有自己的参数，需要根据数据进行优化以获得最佳性能。参数优化技术包括：

- **网格搜索：**系统地遍历参数值的网格，选择最佳组合。
- **贝叶斯优化：**一种基于概率论的优化算法，可以更有效地探索参数空间。
- **遗传算法：**一种基于生物进化的优化算法，可以找到参数的全局最优值。

### 3.3 模型评估和结果解释

**模型评估**

模型评估是验证预测模型性能的关键步骤。常用的评估指标包括：

- **均方根误差（RMSE）：**预测值与实际值之间的平均平方根误差。
- **平均绝对误差（MAE）：**预测值与实际值之间的平均绝对误差。
- **R平方（R²）：**预测值与实际值之间相关性的平方。

**结果解释**

评估结果应仔细解释，以了解模型的预测能力和局限性。解释应包括：

- **模型的准确性：**评估指标的含义和模型在不同预测范围内的性能。
- **模型的鲁棒性：**模型对数据变化和异常值的敏感性。
- **模型的可解释性：**模型预测的逻辑和特征重要性的理解。

# 4. 时间序列预测模型的优化技巧

### 4.1 数据转换和特征选择

#### 数据转换

数据转换是指将原始数据转换为更适合预测模型的形式。常见的数据转换技术包括：

- **对数转换：**将正值数据转换为对数形式，以减轻异常值的影响。
- **归一化：**将数据缩放到 0 到 1 之间的范围，以提高模型的稳定性。
- **差分：**计算相邻数据点的差值，以消除趋势和季节性。

**代码示例：**

import numpy as np

# 对数转换
log_data = np.log(data)

# 归一化
normalized_data = (data - data.min()) / (data.max() - data.min())

# 差分
diff_data = np.diff(data)

#### 特征选择

特征选择是指从原始数据中选择与预测目标最相关的特征。常见的方法包括：

- **相关性分析：**计算特征与目标变量之间的相关性，选择相关性较高的特征。
- **互信息：**衡量特征与目标变量之间的信息依赖性，选择互信息较高的特征。
- **递归特征消除（RFE）：**逐次移除对预测模型贡献最小的特征，直到达到所需的特征数量。

**代码示例：**

from sklearn.feature_selection import SelectKBest, chi2

# 相关性分析
corr = data.corr()
selected_features = corr['target'].sort_values(ascending=False).index[:5]

# 互信息
from sklearn.feature_selection import mutual_info_classif
selected_features = mutual_info_classif(data, target)

# 递归特征消除
from sklearn.feature_selection import RFE
selector = RFE(estimator, n_features_to_select=5)
selector.fit(data, target)
selected_features = data.columns[selector.support_]

### 4.2 模型集成和组合

#### 模型集成

模型集成是指将多个预测模型的预测结果进行组合，以提高预测精度。常见的集成方法包括：

- **平均集成：**对多个模型的预测结果取平均值。
- **加权平均集成：**根据每个模型的性能，为其预测结果分配不同的权重，然后取加权平均值。
- **堆叠集成：**将多个模型的预测结果作为输入，训练一个新的模型进行最终预测。

**代码示例：**

from sklearn.ensemble import VotingClassifier

# 平均集成
voting_classifier = VotingClassifier(estimators=[model1, model2, model3], voting='hard')
voting_classifier.fit(data, target)
predictions = voting_classifier.predict(new_data)

# 加权平均集成
voting_classifier = VotingClassifier(estimators=[model1, model2, model3], voting='soft')
voting_classifier.fit(data, target)
predictions = voting_classifier.predict(new_data)

# 堆叠集成
meta_model = LogisticRegression()
meta_model.fit(np.hstack([model1.predict(data), model2.predict(data), model3.predict(data)]), target)
predictions = meta_model.predict(np.hstack([model1.predict(new_data), model2.predict(new_data), model3.predict(new_data)]))

#### 模型组合

模型组合是指将不同类型的预测模型进行组合，以利用它们的优势。常见的组合方法包括：

- **串行组合：**将多个模型串联起来，每个模型的输出作为下一个模型的输入。
- **并行组合：**将多个模型并行运行，然后对它们的预测结果进行组合。
- **混合组合：**将集成和组合方法相结合，以创建更复杂的模型结构。

**代码示例：**

# 串行组合
model1 = ARIMA(data, order=(5, 1, 0))
model2 = LSTM(data, batch_size=32, epochs=100)
predictions = model2.predict(model1.predict(new_data))

# 并行组合
model1 = ARIMA(data, order=(5, 1, 0))
model2 = LSTM(data, batch_size=32, epochs=100)
predictions = (model1.predict(new_data) + model2.predict(new_data)) / 2

# 混合组合
voting_classifier = VotingClassifier(estimators=[model1, model2], voting='soft')
meta_model = LogisticRegression()
meta_model.fit(voting_classifier.predict(data), target)
predictions = meta_model.predict(voting_classifier.predict(new_data))

### 4.3 超参数调优和贝叶斯优化

#### 超参数调优

超参数调优是指调整模型的超参数，以找到最优的模型性能。常见的超参数调优方法包括：

- **网格搜索：**系统地遍历超参数的预定义值范围，并选择性能最佳的组合。
- **随机搜索：**随机采样超参数值，并选择性能最佳的组合。
- **贝叶斯优化：**利用贝叶斯统计，逐步更新超参数分布，并选择最优的超参数组合。

**代码示例：**

from sklearn.model_selection import GridSearchCV

# 网格搜索
param_grid = {'learning_rate': [0.01, 0.001], 'batch_size': [32, 64]}
grid_search = GridSearchCV(model, param_grid, cv=5)
grid_search.fit(data, target)
best_params = grid_search.best_params_

# 随机搜索
from sklearn.model_selection import RandomizedSearchCV

param_distributions = {'learning_rate': [0.01, 0.001], 'batch_size': [32, 64]}
random_search = RandomizedSearchCV(model, param_distributions, cv=5)
random_search.fit(data, target)
best_params = random_search.best_params_

# 贝叶斯优化
from bayes_opt import BayesianOptimization

def objective(params):
    model.set_params(**params)
    return -model.score(data, target)

optimizer = BayesianOptimization(objective, {'learning_rate': (0.001, 0.1), 'batch_size': (32, 128)})
optimizer.maximize(n_iter=10)
best_params = optimizer.max['params']

#### 贝叶斯优化

贝叶斯优化是一种基于贝叶斯统计的超参数调优方法。它通过逐步更新超参数分布，并在每个步骤中选择最优的超参数组合，来找到最优的模型性能。

贝叶斯优化流程如下：

1. 初始化超参数分布和先验知识。
2. 采样超参数组合，并使用模型评估性能。
3. 更新超参数分布，以反映观察到的性能。
4. 重复步骤 2 和 3，直到达到终止条件。

**代码示例：**

from bayes_opt import BayesianOptimization

def objective(params):
    model.set_params(**params)
    return -model.score(data, target)

optimizer = BayesianOptimization(objective, {'learning_rate': (0.001, 0.1), 'batch_size': (32, 128)})
optimizer.maximize(n_iter=10)
best_params = optimizer.max['params']

# 5. 时间序列预测模型的进阶应用

### 5.1 多变量时间序列预测

**引言**

时间序列预测模型通常用于预测单个变量的时间序列数据。然而，在现实世界中，许多问题涉及多个相互关联的变量。多变量时间序列预测模型旨在同时预测多个变量的时间序列数据，考虑变量之间的关系。

**方法**

多变量时间序列预测模型可以采用各种方法，包括：

- **向量自回归（VAR）模型：**一种线性模型，预测每个变量的当前值基于其自身过去值和所有其他变量的过去值。
- **向量自回归移动平均（VARMA）模型：**扩展 VAR 模型，包括移动平均项。
- **向量自回归积分移动平均（VARIMA）模型：**进一步扩展 VARMA 模型，包括差分项。
- **动态因子模型（DFM）：**一种基于因子分析的模型，将多个时间序列分解为少数潜在因子。

**应用**

多变量时间序列预测模型广泛应用于：

- 经济预测（预测 GDP、通胀、失业率）
- 金融预测（预测股票价格、汇率）
- 医疗保健预测（预测疾病传播、患者结果）

### 5.2 时间序列异常检测和故障诊断

**引言**

时间序列异常检测是指识别时间序列数据中与正常模式显着不同的数据点或子序列。故障诊断是确定异常的根本原因的过程。

**方法**

时间序列异常检测和故障诊断方法包括：

- **统计方法：**基于统计度量（例如，均值、标准差）检测异常。
- **机器学习方法：**使用监督或无监督机器学习算法检测异常。
- **基于模型的方法：**使用时间序列预测模型来检测偏离预测值的异常。

**应用**

时间序列异常检测和故障诊断在以下领域至关重要：

- 制造业（检测设备故障）
- 金融（检测欺诈交易）
- 医疗保健（检测疾病爆发）

**案例研究**

**案例 1：多变量时间序列预测**

一家零售公司希望预测其不同商店的每日销售额。使用 VAR 模型，公司可以同时预测所有商店的销售额，考虑商店之间的相关性。

**案例 2：时间序列异常检测**

一家制造公司希望检测其机器中的异常振动模式。使用基于模型的方法，公司可以建立一个振动时间序列预测模型，并检测偏离预测值的异常，从而识别潜在的故障。

# 6.1 模型验证和部署

在开发和优化时间序列预测模型之后，至关重要的是对其进行验证和部署，以确保其在实际环境中的有效性和鲁棒性。

### 模型验证

模型验证是评估预测模型在未见数据上的性能的过程。它涉及将模型应用于独立的数据集，该数据集未用于训练或优化模型。这有助于识别过拟合问题并确保模型能够泛化到新数据。

### 部署

一旦模型经过验证，就可以将其部署到生产环境中。部署过程涉及将模型集成到应用程序或系统中，以便它可以对实时数据进行预测。

### 持续监控和改进

部署模型后，持续监控其性能非常重要。这包括跟踪预测准确性、模型漂移和任何可能影响模型性能的变化。根据监控结果，可以采取措施改进模型，例如重新训练、调整超参数或集成新的数据。

### 代码示例

以下 Python 代码演示了如何使用 Scikit-Learn 库部署时间序列预测模型：

# 导入必要的库
from sklearn.externals import joblib

# 加载训练好的模型
model = joblib.load('my_model.pkl')

# 部署模型
while True:
    # 获取新数据
    new_data = ...

    # 对新数据进行预测
    predictions = model.predict(new_data)

    # 使用预测结果
    ...

### 流程图

下图展示了时间序列预测模型验证和部署的流程：

graph LR
subgraph 模型验证
    A[训练数据集] --> B[模型训练] --> C[模型验证]
end
subgraph 模型部署
    D[模型验证] --> E[模型部署]
end
subgraph 持续监控和改进
    F[模型部署] --> G[模型监控] --> H[模型改进]
end