时间序列预测模型在金融领域的应用:预测股市趋势的利器
发布时间: 2024-08-23 02:11:22 阅读量: 37 订阅数: 33 


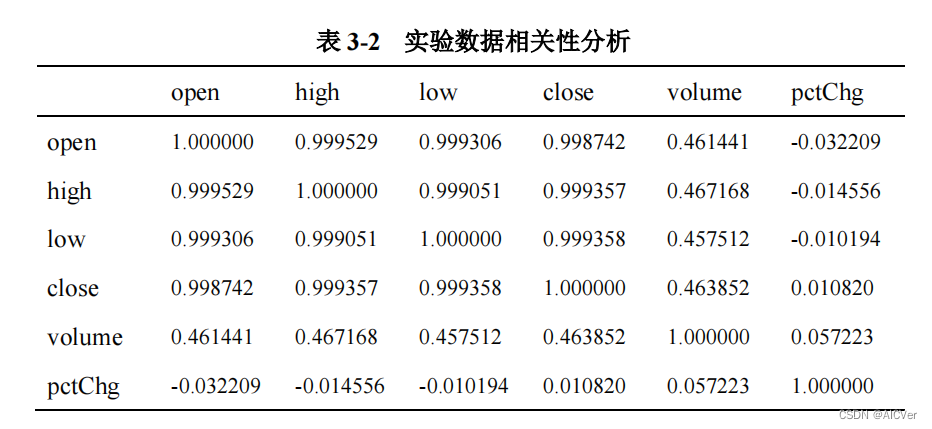
时间序列模型在预测领域的应用及案例分析
# 1. 时间序列预测模型概述
时间序列预测模型是一种用于预测未来值的时间序列数据分析技术。时间序列数据是指随着时间推移而收集的一系列数据点,具有时间依赖性的特点。时间序列预测模型通过分析历史数据中的模式和趋势,来预测未来的值。
时间序列预测模型在金融、经济、气象等领域有着广泛的应用。在金融领域,时间序列预测模型可以用于预测股市趋势、金融风险评估等。在经济领域,时间序列预测模型可以用于预测经济增长、通货膨胀等。在气象领域,时间序列预测模型可以用于预测天气变化、自然灾害等。
# 2. 时间序列预测模型的理论基础
### 2.1 时间序列的特征和分解
#### 2.1.1 时间序列的平稳性
时间序列的平稳性是指其统计特性随着时间的推移而保持相对稳定。平稳时间序列具有以下特征:
- **均值平稳:**时间序列的均值在一段时间内保持恒定。
- **方差平稳:**时间序列的方差在一段时间内保持恒定。
- **自相关平稳:**时间序列的协方差在不同的时间间隔内保持恒定。
平稳时间序列对于预测至关重要,因为它们可以被建模为具有恒定统计特性的随机过程。
#### 2.1.2 时间序列的分解
时间序列可以分解为以下几个分量:
- **趋势分量:**表示时间序列的长期趋势。
- **季节分量:**表示时间序列中与特定时间段(如季节)相关的周期性变化。
- **残差分量:**表示时间序列中无法用趋势和季节分量解释的随机波动。
时间序列分解对于识别和分离时间序列中的不同模式非常重要。
### 2.2 时间序列预测模型的分类
时间序列预测模型可以分为两大类:
#### 2.2.1 线性模型
线性模型假设时间序列可以表示为一个线性方程的解。常见的线性模型包括:
- **自回归移动平均(ARMA)模型:**将时间序列表示为其过去值的线性组合和随机误差项的移动平均。
- **自回归综合移动平均(ARIMA)模型:**在ARMA模型的基础上,对时间序列进行差分以使其平稳。
#### 2.2.2 非线性模型
非线性模型允许时间序列与过去值的非线性关系。常见的非线性模型包括:
- **神经网络:**使用多层神经元网络来学习时间序列中的复杂模式。
- **支持向量机:**使用超平面将时间序列划分为不同的类别。
- **决策树:**使用一系列决策规则将时间序列划分为不同的组。
**代码块:**
```python
import statsmodels.api as sm
# 导入时间序列数据
data = sm.datasets.sunspots.load_pandas().data
# 分解时间序列
decomposition = sm.tsa.seasonal_decompose(data['SUNACTIVITY'], model='additive')
# 绘制分解后的分量
decomposition.plot()
plt.show()
```
**逻辑分析:**
此代码块使用Statsmodels库分解时间序列。`seasonal_decompose`函数将时间序列分解为趋势、季节和残差分量。`plot`函数可视化分解后的分量。
**参数说明:**
- `model`:分解模型,可以是“加法”或“乘法”。
- `period`:季节分量的周期,对于月度数据通常为12。
# 3. 时间序列预测模型在金融领域的应用
时间序列预测模型在金融领域有着广泛的应用,主要用于预测股市趋势和评估金融风险。
### 3.1 股市趋势预测
股市趋势预测是金融领域最常见的应用之一。通过分析历史股价数据,时间序列预测模型可以预测未来股价走势,为投资者提供决策依据。
#### 3.1.1 技术分析指标
技术分析指标是基于历史价格数据计算得出的指标,用于分析股价趋势和预测未来走势。常见的技术分析指标包括:
- **移动平均线(MA):**计算一段时间内股价的平均值,用于识别趋势和支撑/阻力位。
- **相对强弱指标(RSI):**衡量股价上涨和下跌的相对强度,用于识别超买和超卖区域。
- **布林带(Bollinger Bands):**计算股价的标准差,形成上下两条带,用于识别趋势和波动性。
#### 3.1.2 基本面分析
基本面分析是通过分析公司的财务状况、行业趋势和经济环境等因素来预测股价走势。基本面分析指标包括:
- **市盈率(P/E):**股价与每股收益的比率,用于评估公司的估值。
- **市净率(P/B):**股价
0
0





