时间序列预测模型与其他预测方法的比较：探索不同的预测技术

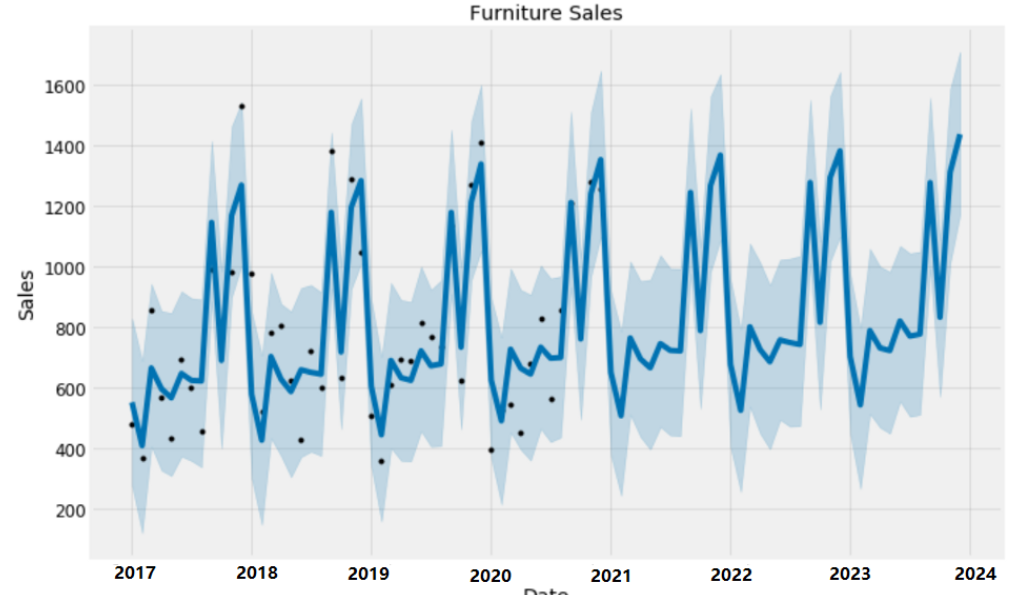
# 1. 时间序列预测模型概述

时间序列预测模型是一种统计模型，用于预测未来基于历史数据的时间序列。这些模型利用时间序列中固有的模式和趋势来生成预测值。时间序列预测模型广泛应用于各种领域，包括金融、供应链管理和医疗保健。

时间序列预测模型通常分为两大类：参数模型和非参数模型。参数模型假设时间序列遵循特定概率分布，例如正态分布或泊松分布。非参数模型不假设任何特定分布，而是根据数据本身的特征进行预测。

# 2. 时间序列预测模型与其他预测方法的对比

时间序列预测模型在预测未来趋势方面具有独特的优势，但并非所有预测问题都适合使用时间序列预测模型。在某些情况下，其他预测方法可能更适合。本节将比较时间序列预测模型与其他常见预测方法，包括线性回归模型、自回归滑动平均模型（ARMA）和霍尔特-温特斯指数平滑模型。

### 2.1 线性回归模型

#### 2.1.1 线性回归原理

线性回归模型是一种统计模型，用于预测一个或多个自变量与一个因变量之间的线性关系。线性回归模型的方程为：

y = β0 + β1x1 + β2x2 + ... + βnxn + ε

其中：

* y 是因变量
* x1, x2, ..., xn 是自变量
* β0, β1, ..., βn 是模型参数
* ε 是误差项

线性回归模型假设自变量和因变量之间的关系是线性的，并且误差项是正态分布的。

#### 2.1.2 线性回归建模步骤

线性回归建模步骤如下：

1. 收集数据：收集自变量和因变量的数据。
2. 数据预处理：对数据进行预处理，包括数据清洗、转换和标准化。
3. 模型训练：使用训练数据训练线性回归模型，估计模型参数。
4. 模型评估：使用验证数据评估模型的性能，计算模型的准确度和误差。
5. 模型部署：将训练好的模型部署到生产环境中，用于预测新的数据。

### 2.2 自回归滑动平均模型（ARMA）

#### 2.2.1 ARMA模型原理

自回归滑动平均模型（ARMA）是一种时间序列预测模型，用于预测时间序列数据的未来值。ARMA模型的方程为：

y(t) = φ1y(t-1) + φ2y(t-2) + ... + φpy(t-p) + ε(t) + θ1ε(t-1) + θ2ε(t-2) + ... + θqε(t-q)

其中：

* y(t) 是时间序列数据在时间 t 的值
* φ1, φ2, ..., φp 是自回归系数
* θ1, θ2, ..., θq 是滑动平均系数
* ε(t) 是白噪声误差项

ARMA模型假设时间序列数据是一个自回归滑动平均过程，即未来的值取决于过去的值和误差项。

#### 2.2.2 ARMA模型参数估计

ARMA模型的参数可以通过最大似然估计法估计。最大似然估计法通过最大化似然函数来估计模型参数，似然函数是模型在给定观测数据下的概率。

### 2.3 霍尔特-温特斯指数平滑模型

#### 2.3.1 霍尔特-温特斯指数平滑原理

霍尔特-温特斯指数平滑模型是一种时间序列预测模型，用于预测具有趋势和季节性的时间序列数据。霍尔特-温特斯指数平滑模型的方程为：

y(t) = α(t-1) + β(t-1)(t-1) + γ(t-1)S(t-m) + ε(t)

其中：

* y(t) 是时间序列数据在时间 t 的值
* α(t-1) 是平滑后的水平分量
* β(t-1) 是平滑后的趋势分量
* γ(t-1) 是平滑后的季节分量
* S(t-m) 是 m 期前的季节分量
* ε(t) 是白噪声误差项

霍尔特-温特斯指数平滑模型假设时间序列数