时间序列预测模型评估指南：衡量模型好坏的5大黄金标准

# 1. 时间序列预测模型评估概述

时间序列预测模型评估是衡量模型性能和选择最佳模型的关键步骤。通过评估，我们可以了解模型的预测准确性、稳定性和泛化能力。

**评估目标：**

* 确定模型预测与实际值之间的误差程度
* 比较不同模型的性能，选择最优模型
* 识别模型的优势和劣势，指导模型改进

**评估原则：**

* **客观性：**评估过程应基于数据和统计方法，避免主观因素干扰
* **全面性：**评估指标应涵盖模型的各个方面，包括准确性、稳定性、泛化能力等
* **可解释性：**评估结果应易于理解和解释，为模型选择和改进提供指导

# 2. 模型评估的理论基础

### 2.1 预测误差的度量

在评估时间序列预测模型时，预测误差的度量是至关重要的。它衡量了预测值与实际值之间的差异，为模型的准确性和可靠性提供了一个定量的指标。以下是一些常用的预测误差度量：

#### 2.1.1 均方误差（MSE）

MSE 是预测误差最常用的度量之一。它计算预测值与实际值之间的平方差的平均值。MSE 的公式为：

MSE = (1/n) * Σ(y_i - y_hat_i)^2

其中：

* n 是预测值的数量
* y_i 是实际值
* y_hat_i 是预测值

MSE 的优点是它易于计算和解释。较小的 MSE 值表示更好的预测准确性。

#### 2.1.2 平均绝对误差（MAE）

MAE 计算预测值与实际值之间的绝对差的平均值。MAE 的公式为：

MAE = (1/n) * Σ|y_i - y_hat_i|

MAE 的优点是它对异常值不敏感。与 MSE 相比，MAE 更适合于分布不均匀或包含异常值的数据集。

#### 2.1.3 平均绝对百分比误差（MAPE）

MAPE 计算预测值与实际值的绝对百分比误差的平均值。MAPE 的公式为：

MAPE = (1/n) * Σ|(y_i - y_hat_i) / y_i| * 100%

MAPE 的优点是它可以比较不同规模数据集的预测误差。它适用于实际值始终为正的数据集。

### 2.2 模型选择的统计检验

除了预测误差的度量之外，统计检验还可以帮助选择最佳的时间序列预测模型。以下是一些常用的统计检验：

#### 2.2.1 交叉验证

交叉验证是一种评估模型泛化能力的统计技术。它将数据集划分为多个子集（称为折），然后依次使用每个折作为测试集，其余折作为训练集。通过计算每个折上的预测误差，可以得到模型的平均预测误差。

#### 2.2.2 信息准则（AIC、BIC）

信息准则（例如 AIC 和 BIC）是用于模型选择的统计量。它们平衡了模型的拟合度和复杂度。AIC 的公式为：

AIC = 2k - 2ln(L)

BIC 的公式为：

BIC = k * ln(n) - 2ln(L)

其中：

* k 是模型参数的数量
* n 是数据集的大小
* L 是模型的似然函数

AIC 和 BIC 较小的模型更受青睐。

# 3. 模型评估的实践应用

### 3.1 误差可视化

#### 3.1.1 时间序列图

时间序列图是一种可视化时间序列数据的常用方法。它将时间序列数据绘制成一条线，横轴表示时间，纵轴表示数据值。通过观察时间序列图，我们可以直观地了解数据的趋势、季节性、异常值等特征。

**示例：**

import matplotlib.pyplot as plt

# 导入时间序列数据
data = pd.read_csv('time_series_data.csv')

# 绘制时间序列图
plt.plot(data['date'], data['value'])
plt.xlabel('Date')
plt.ylabel('Value')
plt.title('Time Series Plot')
plt.show()

**逻辑分析：**

这段代码使用 Matplotlib 库绘制了时间序列图。`pd.read_csv()` 函数从 CSV 文件中导入数据，`plt.plot()` 函数将数据绘制成一条线，`plt.xlabel()` 和 `plt.ylabel()` 函数设置横轴和纵轴标签，`plt.title()` 函数设置图表标题，最后 `plt.show()` 函数显示图表。

#### 3.1.2 残差图

残差图是将预测值与实际值之间的差值（残差）绘制成图。通过观察残差图，我们可以判断模型预测的准确性，以及是否存在系统性误差。

**示例：**

import statsmodels.api as sm

# 拟合时间序列模型
model = sm.tsa.statespace.SARIMAX(data, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
model_fit = model.fit()

# 计算残差
residuals = model_fit.resid

# 绘制残差图
plt.plot(residuals)
plt.xlabel('Time')
plt.ylabel('Residual')
plt.title('Residual Plot')
plt.show()

**逻辑分析：**

这段代码使用 Statsmodels 库拟合了一个 SARIMAX 时间序列模型，并计算了残差。`sm.tsa.statespace.SARIMAX()` 函数创建 SARIMAX 模型，`model.fit()` 函数拟合模型，`model_fit.resid` 属性返回残差，最后 `plt.plot()` 函数绘制残差图。

### 3.2 模型比较和选择

#### 3.2.1 嵌套交叉验证

嵌套交叉验证是一种用于模型选择和超参数优化的交叉验证方法。它将数据分成多个外部折，然后在每个外部折上执行内部交叉验证来选择最佳超参数。

**示例：**

from sklearn.model_selection import GridSearchCV, cross_val_score

# 定义超参数网格
param_grid = {'order': [(1, 1, 1), (2, 1, 1), (1, 2, 1)], 'seasonal_order': [(1, 1, 1, 12), (2, 1, 1, 12), (1, 2, 1, 12)]}

# 嵌套交叉验证
nested_cv = GridSearchCV(model, param_grid, cv=5, inner_cv=5)
nested_cv.fit(data)

# 获取最佳超参数
best_params = nested_cv.best_params_

**逻辑分析：**

这段代码使用 Scikit-Learn 库执行嵌套交叉验证。`GridSearchCV()` 函数创建超参数网格搜索对象，`param_grid` 字典指定超参数网格，`cv` 参数指定外部折的数量，`inner_cv` 参数指定内部折的数量，`fit()` 函数拟合模型，最后 `best_params_` 属性返回最佳超参数。

#### 3.2.2 帕累托前沿分析

帕累托前沿分析是一种用于模型比较和选择的多目标优化方法。它将多个评估指标组合成一个单一的度量，并选择在所有指标上都表现良好的模型。

**示例：**

import numpy as np
import matplotlib.pyplot as plt

# 计算多个评估指标
mse = np.mean((data['actual'] - data['predicted']) ** 2)
mae = np.mean(np.abs(data['actual'] - data['predicted']))
mape = np.mean(np.abs((data['actual'] - data['predicted']) / data['actual']))

# 创建帕累托前沿
plt.scatter(mse, mae)
plt.xlabel('MSE')
plt.ylabel('MAE')
plt.title('Pareto Front')
plt.show()

**逻辑分析：**

这段代码使用 NumPy 和 Matplotlib 库计算了多个评估指标，并创建了帕累托前沿。`np.mean()` 函数计算平均值，`np.abs()` 函数计算绝对值，`plt.scatter()` 函数绘制散点图，`plt.xlabel()` 和 `plt.ylabel()` 函数设置横轴和纵轴标签，`plt.title()` 函数设置图表标题，最后 `plt.show()` 函数显示图表。

# 4. 模型评估的进阶技巧

### 4.1 时间序列分解

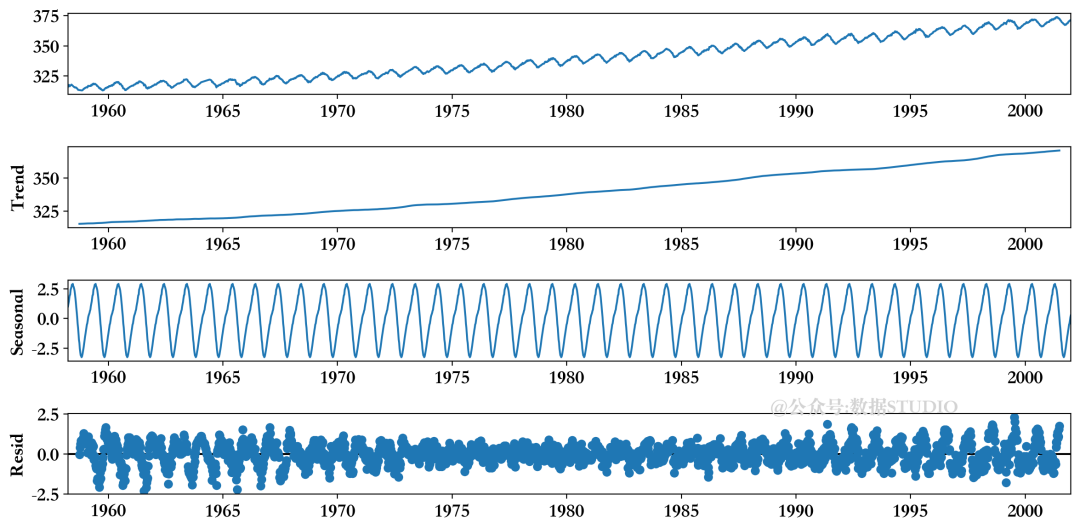
#### 4.1.1 分解方法（趋势、季节性、残差）

时间序列分解是一种将时间序列分解为趋势、季节性和残差分量的技术。这有助于深入了解数据模式，并为模型评估提供更细粒度的视角。

* **趋势：**代表数据随时间推移的长期变化。
* **季节性：**代表数据中可预测的周期性模式，例如每天、每周或每年。
* **残差：**代表无法由趋势和季节性解释的剩余变化。

常用的分解方法包括：

* **加法分解：**时间序列 = 趋势 + 季节性 + 残差
* **乘法分解：**时间序列 = 趋势 * 季节性 * 残差

#### 4.1.2 分解后模型评估

时间序列分解后，可以对每个分量单独进行模型评估。这有助于识别模型在捕捉不同模式方面的优缺点。例如：

* **趋势模型评估：**使用均方误差（MSE）或平均绝对误差（MAE）评估模型对趋势的预测准确性。
* **季节性模型评估：**使用平均绝对百分比误差（MAPE）或交叉相关系数评估模型对季节性模式的预测准确性。
* **残差模型评估：**使用白噪声检验或自相关检验评估残差是否具有随机性。

### 4.2 滚动预测评估

#### 4.2.1 滚动预测窗口

滚动预测评估是一种在时间序列上动态评估模型性能的方法。它涉及将预测窗口向前滚动，并在每个时间点上重新训练模型并进行预测。

滚动预测窗口的大小取决于时间序列的性质和预测目标。较大的窗口提供更稳定的预测，但对数据变化的响应较慢。较小的窗口对数据变化更敏感，但预测可能更不稳定。

#### 4.2.2 滚动预测误差

滚动预测误差是使用滚动预测窗口预测的实际值和预测值之间的差异。它可以用于评估模型随时间推移的性能，并识别模型在不同数据条件下的优缺点。

滚动预测误差的常见度量包括：

* **滚动均方误差（RMSE）：**滚动预测窗口内预测误差的平方和的平均值。
* **滚动平均绝对误差（MAE）：**滚动预测窗口内预测误差的绝对值的平均值。
* **滚动平均绝对百分比误差（MAPE）：**滚动预测窗口内预测误差的绝对百分比的平均值。

**代码块：**

import numpy as np
from sklearn.model_selection import TimeSeriesSplit

# 加载时间序列数据
data = np.loadtxt('time_series_data.csv', delimiter=',')

# 设置滚动预测窗口大小
window_size = 12

# 创建滚动预测评估器
tscv = TimeSeriesSplit(n_splits=5, max_train_size=window_size)

# 滚动预测评估
for train_index, test_index in tscv.split(data):
    # 训练模型
    model = ...

    # 预测
    predictions = ...

    # 计算滚动预测误差
    rmse = np.sqrt(np.mean((predictions - data[test_index]) ** 2))
    mae = np.mean(np.abs(predictions - data[test_index]))
    mape = np.mean(np.abs((predictions - data[test_index]) / data[test_index]) * 100)

    # 打印滚动预测误差
    print(f'RMSE: {rmse}, MAE: {mae}, MAPE: {mape}')

**逻辑分析：**

该代码使用 `TimeSeriesSplit` 交叉验证器创建滚动预测评估器。评估器将数据分成训练集和测试集，训练集大小为滚动预测窗口大小。然后，模型在每个训练集上进行训练，并在相应的测试集上进行预测。滚动预测误差（RMSE、MAE、MAPE）在每个滚动中计算，并打印出来。

**参数说明：**

* `n_splits`：交叉验证的折叠数。
* `max_train_size`：训练集的最大大小（滚动预测窗口大小）。

# 5. 模型评估的最佳实践**

### 5.1 评估指标的选择

选择合适的评估指标对于时间序列预测模型的评估至关重要。不同的指标侧重于不同的误差类型，因此根据模型的特定目的和目标进行选择很重要。

| 评估指标 | 侧重点 |
|---|---|
| 均方误差（MSE） | 绝对误差的平方和 |
| 平均绝对误差（MAE） | 绝对误差的平均值 |
| 平均绝对百分比误差（MAPE） | 绝对百分比误差的平均值 |
| 交叉验证 | 模型泛化能力的评估 |
| 信息准则（AIC、BIC） | 模型复杂性和预测性能之间的权衡 |

### 5.2 评估过程的自动化

随着时间序列数据的不断增长，手动评估模型变得不可行。自动化评估过程可以节省时间和精力，同时确保评估的一致性和可靠性。

可以使用 Python 等编程语言编写脚本或利用机器学习库（如 scikit-learn）中的内置评估函数来实现自动化。

from sklearn.metrics import mean_squared_error

# 加载时间序列数据
data = pd.read_csv('data.csv')

# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(data['features'], data['target'], test_size=0.2)

# 训练模型
model = TimeSeriesModel()
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)

# 计算 MSE
mse = mean_squared_error(y_test, y_pred)

### 5.3 评估结果的解释和报告

评估结果的解释和报告对于理解模型的性能和做出明智的决策至关重要。

解释评估结果时，应考虑以下因素：

* 误差的幅度和类型
* 模型的泛化能力
* 与基线模型或其他模型的比较
* 评估结果对业务决策的影响

报告评估结果时，应包括以下信息：

* 所使用的评估指标
* 评估结果（误差值、统计检验结果等）
* 对结果的解释和建议