【环形二叉树结构】：探索JavaScript中的高级环形数据结构

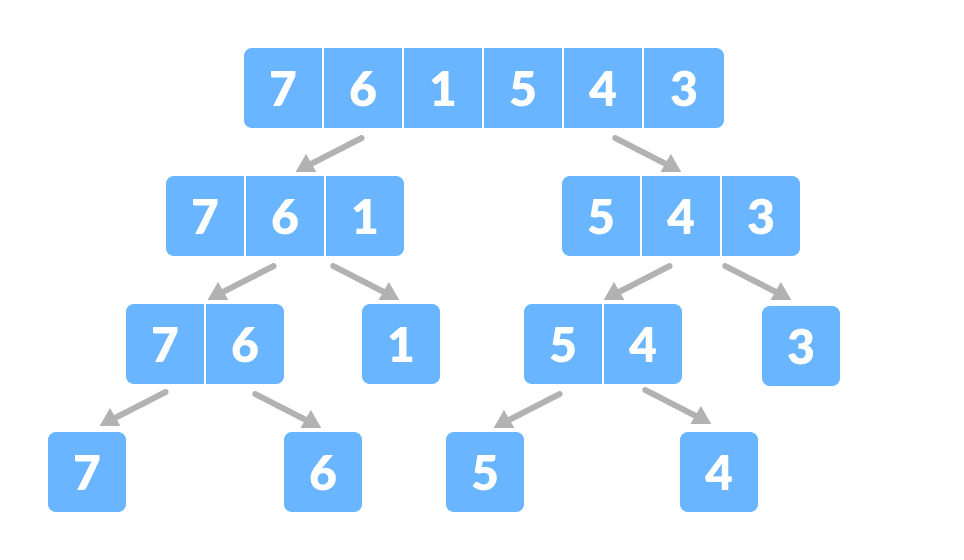
# 1. 环形二叉树结构概述

环形二叉树作为一种创新的数据结构，它将传统的二叉树与环形数据结构结合，形成了一种既有层次分明的树形结构特性，又具备循环利用空间优势的数据组织方式。这种结构在处理特定问题，如存储大量动态数据时，能显著提高存储效率和访问速度。

在本章节，我们将对环形二叉树的基本概念进行简单介绍，并说明其与传统二叉树的区别与优势，为读者提供一个对环形二叉树的初步理解。在此基础上，后续章节将深入探讨环形二叉树的理论基础、实现细节、应用实例及性能优化，以全面揭示其作为数据结构研究的新领域所具有的实用价值和学术意义。

# 2. 环形二叉树的理论基础

## 2.1 二叉树的基本概念

### 2.1.1 二叉树的定义和性质

二叉树是一种特殊的数据结构，它是每个节点最多有两个子节点的树结构。在二叉树中，子节点被区分称为左子节点和右子节点。尽管概念上简单，但二叉树在计算机科学中有着广泛的应用，因为它们能够有效地组织数据，进行搜索、排序和各种其他操作。

在二叉树的定义中，有几个关键的性质：

- **节点的度**：在二叉树中，任何节点的度最多为2。
- **叶子节点**：没有子节点的节点称为叶子节点。
- **深度与高度**：节点的深度是从根节点开始，沿着树向下到达该节点的边数。节点的高度是从该节点出发，向上到达根节点的最长路径的边数。

二叉树的这些基本性质是设计和分析复杂算法的基础，无论是在单线程还是多线程环境下。

### 2.1.2 二叉树的遍历算法

遍历算法是二叉树算法的核心，其中三种主要的遍历方式为：前序遍历、中序遍历、后序遍历。

- **前序遍历**：首先访问根节点，然后是左子树，最后是右子树。
- **中序遍历**：先访问左子树，然后是根节点，最后是右子树。
- **后序遍历**：先访问左子树，然后是右子树，最后是根节点。

每种遍历方式都有其独特的应用场景。例如，中序遍历用于二叉搜索树，因为它能以排序的方式返回节点值。

# Python示例代码：二叉树的遍历算法实现
class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def preorder_traversal(root):
    if root:
        print(root.value, end=' ')
        preorder_traversal(root.left)
        preorder_traversal(root.right)

def inorder_traversal(root):
    if root:
        inorder_traversal(root.left)
        print(root.value, end=' ')
        inorder_traversal(root.right)

def postorder_traversal(root):
    if root:
        postorder_traversal(root.left)
        postorder_traversal(root.right)
        print(root.value, end=' ')

# 示例使用
# 构建一个简单的二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

# 执行遍历
print("前序遍历:")
preorder_traversal(root)
print("\n中序遍历:")
inorder_traversal(root)
print("\n后序遍历:")
postorder_traversal(root)

在上述代码中，我们定义了一个简单的二叉树节点类TreeNode，并实现了前序、中序和后序遍历的函数。通过递归调用，实现了遍历操作。

## 2.2 环形数据结构的原理

### 2.2.1 环形结构的特点和应用场景

环形结构是一种数据结构，其特点是没有开始也没有结束，数据项首尾相连，形成一个闭合的环。这种结构的特点是循环利用所有节点，没有开始和结束的概念。

环形结构在计算机科学中通常用于实现队列、循环缓冲区或循环链表。在这些场景中，环形结构可以提供更加高效的数据管理方式，特别是在有固定数据量、需要不断循环处理的场景中。

环形结构的一个关键优势是其处理边界条件时的简便性。例如，在一个循环链表中，添加和删除操作的边界条件处理变得非常直观。

### 2.2.2 环形结构在二叉树中的实现

将环形结构的概念应用到二叉树中，我们得到了环形二叉树的概念。这种结构允许我们在二叉树中实现循环遍历，为某些特定的数据处理需求提供了更加灵活的解决方案。

环形二叉树的每个节点都保持了与父节点的链接，使得从任意节点出发，都能够通过遍历到达其他所有节点。在实现时，需要特别注意维护这些环形链接的完整性。

# Python示例代码：环形二叉树节点的构建
class CircularBinaryTreeNode:
    def __init__(self, value=0, parent=None):
        self.value = value
        self.parent = parent
        self.left = None
        self.right = None

    def set_parent(self, parent_node):
        self.parent = parent_node

    def set_left(self, left_node):
        self.left = left_node
        self.left.set_parent(self)

    def set_right(self, right_node):
        self.right = right_node
        self.right.set_parent(self)

# 示例使用
root = CircularBinaryTreeNode(1)
child1 = CircularBinaryTreeNode(2)
child2 = CircularBinaryTreeNode(3)

root.set_left(child1)
root.set_right(child2)

在这个例子中，我们定义了一个环形二叉树节点类CircularBinaryTreeNode，并实现了节点间的链接。通过set_left和set_right方法，可以建立节点间的父子关系，同时保证了环形结构的完整性。

## 2.3