【环形数据结构的性能优化】：提升JavaScript环形数据处理效率

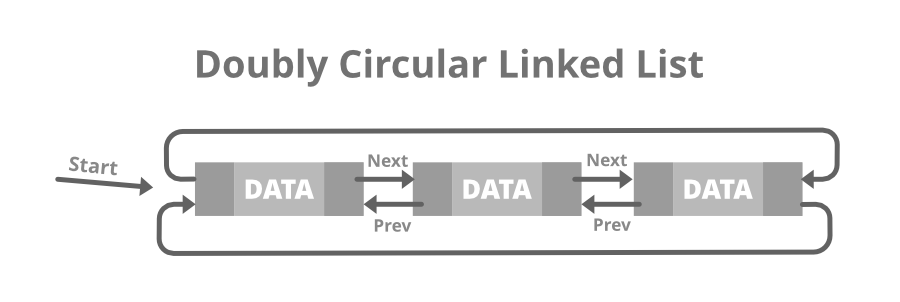
# 1. 环形数据结构概述与应用场景

## 1.1 环形数据结构简介

环形数据结构是一种特殊的数据结构，其特点是元素之间形成一个闭合的环。不像常见的线性结构，如链表或数组，有明确的起点和终点，环形结构中的每个元素都有一个后继元素，形成一个无限循环。这种数据结构在编程中并不多见，但其独特的性质在特定场景下非常有用。

## 1.2 典型应用场景

环形数据结构的应用场景包括但不限于：

- **环形缓冲区**：用于缓存数据流的场景，如在音频或视频播放中实现平滑的播放体验。
- **生产者-消费者模型**：在多线程编程中，生产者线程和消费者线程通过环形结构共享数据，实现高效的线程间通信。
- **时钟算法**：在实现轮转调度系统时，环形数据结构可以提供一种简洁的方式来处理任务的时间片分配。

环形数据结构提供了一种不同于传统线性结构的思考方式，能够有效地解决特定的编程问题。在接下来的章节中，我们将深入探讨环形数据结构的理论基础、实现技巧，以及如何在JavaScript中有效地使用和优化它们。

# 2. JavaScript中环形数据结构的理论基础

环形数据结构是一种在内存中呈环状的数据组织方式，它在解决某些特定类型的问题时，比如实现循环队列、处理历史记录或者管理有限状态机等，显示出其独特的优势。在这一章节中，我们将探索环形数据结构的基础知识，包括其定义、类型、复杂度分析以及在JavaScript中的具体实现方式。

## 2.1 环形数据结构定义和特性

### 2.1.1 环形数据结构的数学模型

环形数据结构可以被抽象为图论中的一个环（Cycle）的概念。从数据结构的视角来看，环形数据结构是一种特殊的线性数据结构，其中最后一个元素的指针指向第一个元素，形成一个封闭的环。数学上，环形结构可以被表示为一个序列，序列中的每个元素都与其前驱和后继元素直接相连。

在计算机科学中，环形结构通常用于需要循环处理的场景，如循环缓冲区、事件驱动的系统等。环形结构的数学模型可以定义为一个有序的元素集合 E = {e1, e2, ..., en}，以及一个映射函数 f：E -> E，满足 f(en) = e1。这样的映射函数建立了集合中元素的循环关系。

### 2.1.2 环形数据结构与线性数据结构的对比

线性数据结构如链表和数组，它们的特性是有一个明确的起点和终点，元素的遍历遵循单向性原则。与之相对，环形数据结构的特点是所有元素形成一个封闭的循环，没有明确的起点和终点，元素的遍历可以在环中无限循环下去。

在实际应用中，环形数据结构与线性数据结构的性能特点也有所不同。例如，在实现缓存机制时，环形队列可以更方便地循环覆盖旧数据，而不是像数组那样需要执行移动元素的操作。然而，环形数据结构也引入了额外的复杂性，例如在查找特定元素或进行插入删除操作时，需要额外的逻辑来维护环的结构。

## 2.2 环形数据结构的类型和实现方式

### 2.2.1 链表实现的环形结构

链表是实现环形数据结构的一种常见方式。在JavaScript中，可以通过创建一个循环链表（circular linked list）来实现。每个节点包含数据和一个指向下个节点的链接，而最后一个节点的链接指向链表的第一个节点。

class Node {
    constructor(data) {
        this.data = data;
        this.next = null;
    }
}

class CircularLinkedList {
    constructor() {
        this.head = null;
    }

    append(data) {
        const newNode = new Node(data);
        if (!this.head) {
            this.head = newNode;
            this.head.next = this.head;
        } else {
            let current = this.head;
            while (current.next !== this.head) {
                current = current.next;
            }
            current.next = newNode;
            newNode.next = this.head;
        }
    }
}

### 2.2.2 数组实现的环形结构

数组也可以用来实现环形数据结构，虽然从内存使用效率上来说，它不如链表灵活。使用数组实现环形结构，通常通过模运算来计算数组中的位置，实现循环访问。

class CircularArray {
    constructor(size) {
        this.size = size;
        this.array = new Array(size);
    }

    get(index) {
        return this.array[index % this.size];
    }

    set(index, value) {
        this.array[index % this.size] = value;
    }
}

### 2.2.3 JavaScript中的实现技巧

在JavaScript中实现环形数据结构，我们通常需要维护一个指针来追踪当前操作的位置，确保操作的连续性和正确性。下面是一个简单的环形数组实现：

class CircularQueue {
    constructor(limit) {
        this.queue = new Array(limit);
        this.limit = limit;
        this.head = 0;
        this.tail = 0;
        this.size = 0;
    }

    enqueue(item) {
        if (this.size < this.limit) {
            this.queue[this.tail] = item;
            this.tail = (this.tail + 1) % this.limit;
            this.size++;
        }
    }

    dequeue() {
        if (this.size > 0) {
            const item = this.queue[this.head];
            this.head = (this.head + 1) % this.limit;
            this.size--;
            return item;
        }
    }
}

## 2.3 环形数据结构的复杂度分析

### 2.3.1 时间复杂度分析

环形数据结构的操作复杂度与实现方式有关。对于链表实现的环形结构，其基本操作，如添加和删除节点，通常具有O(1)的时间复杂度，因为这些操作不需要遍历整个数据结构。然而，查找操作的时间复杂度会受到链表长度的影响，为O(n)。

对于数组实现的环形结构，由于数组的随机访问特性，基本操作的时间复杂度均为O(1)，但需要注意的是，在JavaScript中，数组的某些操作可能会引起数据移动，从而影响性能。

### 2.3.2 空间复杂度分析

环形数据结构的空间复杂度与其实现的方式和存储的数据类型有关。对于链表实现的环形结构，空间复杂度取决于节点的数量，即O(n)。对于数组实现的环形结构，空间复杂度为O(limit)，其中limit是数组的长度。需要注意的是，数组实现可能因为固定大小而产生空间浪费或限制容量。

通过本章的介绍，我们理解了环形数据结构的基本概念、类型、以及它们在JavaScript中的实现方式。在下一章中，我们将进一步探讨环形数据结构在JavaScript中的性能挑战和优化实践。

# 3. 环形数据结构在JavaScript中的性能挑战

环形数据结构在JavaScript中的应用广泛，它能够有效地模拟现实世界中的循环流程，如消息队列、数据缓冲区等。然而，在实际应用中，环形结构面临诸多性能挑战，开发者必须采取相应的优化措施来确保应用的高效性和稳定性。本章将深入探讨这些性能挑战，并展示如何通过理论分析和实践经验来解决这些问题。

## 3.1 常见性能问题

### 3.1.1 内存泄漏的风险

环形数据结构由于其闭合循环的特性，在JavaScript中容易造成内存泄漏。一旦环中的节点无法被外部引用所访问，而又没有适时地被清除，就会导致内存泄漏。这种情况在长时间运行的应用中尤为常见，可能会引起性能下降和应用崩溃。

为了防止内存泄漏，开发者需要确保环形结构中的节点在不再需要时能够被垃圾回收机制正确回收。这通常涉及到显式地从环中移除节点，并将节点的引用设置为null。例如，在使用环形链表时，移除一个节点不仅需要调整前驱节点的next指针，还要确保将被移除节点的next指针指向null，以断开与环的连接。

### 3.1.2 操作效率瓶颈

在环形数据结构中，某些操作如搜索、插入和删除，可能因为需要遍历整个环而变得效率低下。这在大数据量的环形结构中尤为明显，可能导致应用响应缓慢。

为了优化操作效率，开发者可以考虑使用更高效的数据结构，比如引入索引。在环形链表中，可以为每个节点维护一个指向其前驱节点的指针，这样在进行节点删除操作时，只需要调整相邻节点的指针即可，极大地提高了操作效率。

## 3.2 性能优化的理论依据

### 3.2.1 缓存机制的原理与应用

缓存机制是提高数据访问效率的有效手段。在环形数据结构中，可以利用缓存来存储经常访问的数据，以减少重复的查找开销。

缓存策略包括LRU（Least Recently Used）缓存和FIFO（First In First