【MATLAB信号处理实战】：从理论到应用的案例分析

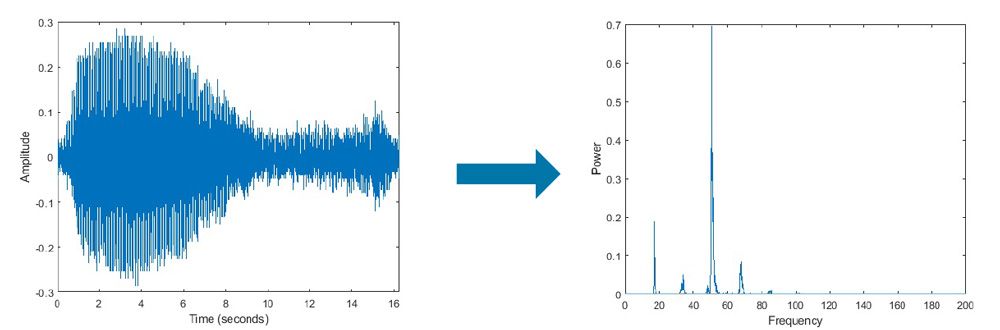
# 1. MATLAB信号处理概述

在当今的工程与科研领域，MATLAB已经成为了不可或缺的工具之一，尤其在信号处理这一分支领域，MATLAB提供了强大的计算和图形能力。本章将带您进入MATLAB信号处理的世界，从理论基础到实践应用，从入门到高级技巧，为您展示如何利用MATLAB解决复杂的信号处理问题。

## 1.1 信号处理的重要性
信号处理是信息科学与工程的核心组成部分，它的主要任务是通过提取有用信息、滤除噪声、增强信号质量等方式，改善数据的可用性和准确性。MATLAB在信号处理领域所提供的功能，让工程师和科研人员能够更加专注于问题的解决，而不是繁琐的计算过程。

## 1.2 MATLAB在信号处理中的优势
MATLAB之所以在信号处理领域广受欢迎，是因为其具备一系列独特的优势：首先，MATLAB拥有丰富、高效的内置函数库，可以大大简化信号处理的复杂度；其次，MATLAB的可视化功能允许用户直观地观察信号处理效果；最后，MATLAB强大的编程能力使得用户能够进行定制化的开发。

## 1.3 探索MATLAB信号处理功能
MATLAB信号处理工具箱集成了大量预先设计好的函数，覆盖了从基本的信号操作到复杂的信号分析与处理技术。本章的后续部分将系统地介绍这些工具箱中的功能，并通过实例展示如何在实际工作中应用它们。

通过本章的学习，您将初步了解MATLAB在信号处理中的作用和特点，为进一步深入学习打下坚实的基础。

# 2. MATLAB信号处理基础理论

## 2.1 数字信号处理基础

### 2.1.1 信号与系统的分类

在数字信号处理中，信号可以被分类为连续时间信号和离散时间信号。连续时间信号是连续变化的，常用于模拟系统中，而离散时间信号是由离散的时间点上的值组成，是数字系统处理的主角。系统的分类也同样基于其处理的信号类型，可以是连续时间系统，也可以是离散时间系统。此外，还有线性系统和非线性系统、时不变系统与时变系统等分类。

% MATLAB 代码示例：离散时间信号的创建
n = 0:10; % 创建一个从0到10的向量，代表离散的时间点
x = sin(2*pi*0.1*n); % 创建一个离散的正弦波信号
stem(n, x); % 使用stem函数绘制信号的图形表示

在这个例子中，我们首先创建了一个离散时间序列`n`，然后生成了一个离散的正弦波信号`x`。使用`stem`函数绘制了信号的图形表示，这样可以直观地看到信号在不同时间点上的值。

### 2.1.2 采样定理与频域分析

根据奈奎斯特定理，要准确地从采样信号中恢复出连续信号，采样频率应至少是信号最高频率的两倍。这是数字信号处理中的基础理论之一，被称为奈奎斯特采样定理。在频域分析中，我们使用傅里叶变换将信号从时域转换到频域，从而分析信号的频率成分。

% MATLAB 代码示例：进行傅里叶变换并绘制频谱图
X = fft(x); % 对信号x进行快速傅里叶变换
n = length(x); % 信号长度
f = (0:n-1)*(1/n); % 生成频率向量
plot(f, abs(X)/n); % 绘制归一化的频谱图

上述代码中，我们使用`fft`函数对信号`x`进行了快速傅里叶变换，得到了信号的频域表示`X`。然后，我们计算了对应的频率向量`f`并绘制了信号的频谱图，这样就可以看到信号的能量在哪些频率上集中。

## 2.2 傅里叶变换及其应用

### 2.2.1 傅里叶级数和傅里叶变换

傅里叶级数用于周期信号，将周期信号表示为不同频率的正弦波和余弦波的无限和。而傅里叶变换则用于非周期信号，可以将其分解为连续的频率成分。它们都基于将复杂信号分解为简单的正弦波和余弦波的原理，这是信号处理中的一个核心概念。

### 2.2.2 快速傅里叶变换（FFT）算法

快速傅里叶变换（FFT）是实现离散傅里叶变换（DFT）的高效算法。FFT极大地减少了计算复杂度，是数字信号处理中不可或缺的工具。通过FFT，可以在较短的时间内完成大规模的频谱分析。

% MATLAB 代码示例：快速傅里叶变换（FFT）
Y = fft(x); % 对信号x进行快速傅里叶变换
N = 2^n; % 确保x的长度为2的幂次
f = (0:N-1)*(Fs/N); % 计算频率向量
plot(f, abs(Y)/N); % 绘制归一化的频谱图

在此段代码中，我们首先对信号`x`进行快速傅里叶变换得到`Y`，接着计算了对应的频率向量`f`。通过绘制`Y`的归一化幅值，我们能够看到信号在频域中的分布情况。

## 2.3 滤波器设计原理

### 2.3.1 滤波器的类型和特性

滤波器是信号处理中的核心组件，用于根据频率选择性地保留或去除信号中的某些成分。滤波器可以分为低通、高通、带通和带阻等类型。它们的特性通常由其频率响应来定义，包括幅度和相位响应。

### 2.3.2 模拟与数字滤波器设计

模拟滤波器基于连续时间的电路原理设计，而数字滤波器则是基于离散时间系统理论。在MATLAB中，数字滤波器的设计可以通过内置的滤波器设计工具箱来完成，也可以使用专用的函数和方法。

% MATLAB 代码示例：设计一个简单的数字低通滤波器
% 使用 butter 函数设计一个低通滤波器
[N, Wn] = buttord(0.1, 0.3, 3, 60); % 计算滤波器的阶数和截止频率
[b, a] = butter(N, Wn); % 根据阶数和截止频率设计滤波器
freqz(b, a); % 绘制滤波器的频率响应图

上述代码通过`butter`函数设计了一个巴特沃斯低通滤波器。我们首先使用`buttord`函数计算滤波器的最小阶数和截止频率，以满足给定的通带和阻带纹波要求。然后，使用`butter`函数实际设计了滤波器，并通过`freqz`函数绘制了滤波器的频率响应图。

## 2.4 小结

在本章中，我们介绍了MATLAB信号处理的基础理论，包括数字信号处理的分类、采样定理和频域分析、傅里叶变换及其在信号处理中的应用，以及滤波器设计原理。理解这些基础理论对深入学习MATLAB信号处理至关重要。在下一章中，我们将探讨这些理论在实践中的应用技巧。

# 3. MATLAB信号处理实践技巧

## 3.1 MATLAB中的信号生成与操作

### 3.1.1 信号的创建与合成

在MATLAB环境中，创建和合成信号是信号处理实践的首要步骤。信号可以是简单的正弦波、方波或更复杂的信号，如人类语音或生物医学信号。利用MATLAB提供的函数，工程师们可以轻松生成这些信号，并进行进一步的分析和处理。

信号生成的最基础函数之一是`sin`函数，用于创建正弦波信号。示例如下：

fs = 1000;             % 采样频率
t = 0:1/fs:1-1/fs;     % 时间向量
f = 5;                 % 信号频率
signal = sin(2*pi*f*t); % 生成5Hz的正弦波信号

这段代码首先定义了采样频率`fs`，然后创建了一个时间向量`t`，并利用正弦函数生成了一个频率为5赫兹的信号。这只是信号创建的一个简单示例。在实际应用中，信号往往是复杂和多样的。例如，一个语音信号可以使用`audioread`函数读取存储在文件中的音频数据：

[signal, fs] = audioread('example.wav'); % 读取一个.wav文件中的音频数据

接下来，可以对这些信号进行修改或合成以产生特定的信号。合成信号时常用的函数有`sum`、`conv`等。

例如，要合成两个不同频率的正弦波信号，可以使用如下代码：

% 生成两个不同频率的正弦波信号
signal1 = sin(2*pi*5*t);
signal2 = sin(2*pi*20*t);

% 合成这两个信号
composite_signal = signal1 + signal2;

合成信号技术在测试信号的创建、信号模拟等场景中非常实用。

### 3.1.2 信号的时间和频率域操作

在MATLAB中，信号既可以进行时间域操作，也可以进行频率域操作。时间域操作通常包括信号的放大、裁剪、平移和缩放等。这些操作有助于改善信号的形态，例如消除噪声或突出信号的特定特征。

频率域操作涉及信号的频谱分析，包括傅里叶变换，它将信号从时间域转换到频率域。快速傅里叶变换（FFT）是进行频谱分析的常用工具。

以下是傅里叶变换和逆变换的简单示例：

% 对信号进行FFT变换
signal_fft = fft(signal);

% 对信号进行逆FFT变换，还原时间域信号
reconstructed_signal = ifft(signal_fft);

进行FFT变换后，我们通常会对结果进行幅值的计算，并绘制出信号的频谱。绘制频谱时，会用到`abs`函数来获取幅值，以及`plot`函数来绘制图形：

% 计算FFT的幅值
magnitude = abs(signal_fft);

% 获取频率向量
n = length(signal);
f = (0:n-1)*(fs/n);

% 绘制信号的频谱
plot(f, magnitude);
title('Signal Spectrum');
xlabel('Frequency (Hz)');
ylabel('Magnitude