MATLAB信号处理中的参数估计与系统辨识

# 1. MATLAB信号处理基础

在数字信号处理的世界里，MATLAB作为一个强大的计算和可视化工具，为工程师和科研人员提供了一个进行算法开发、数据分析、数据可视化及仿真设计的平台。本章旨在为初学者以及有经验的工程师提供一个关于MATLAB在信号处理方面的基础介绍。我们会从信号的表示和分类开始，进而学习信号的变换，最后介绍一些基础的信号处理技术。本章节内容不仅帮助读者理解信号处理的基础概念，还能让读者掌握MATLAB在该领域中的初步应用。

## 1.1 信号的基本概念

信号是信息的载体，可以是连续的或离散的。在MATLAB中，我们主要关注数字信号，即通过采样和量化过程得到的一系列数值。信号可以是确定性的，比如正弦波，也可以是随机性的，如白噪声。

## 1.2 MATLAB中的信号表示

在MATLAB中，信号可以通过向量或矩阵来表示，其中每个元素对应一个采样点。MATLAB提供了一系列函数来进行信号的创建、编辑和操作，比如`sin()`函数可以创建正弦信号，`rand()`可以生成随机噪声信号。

t = 0:0.001:1; % 创建时间向量
f = 5; % 频率设为5Hz
sineSignal = sin(2*pi*f*t); % 创建正弦信号

## 1.3 常用的信号处理技术

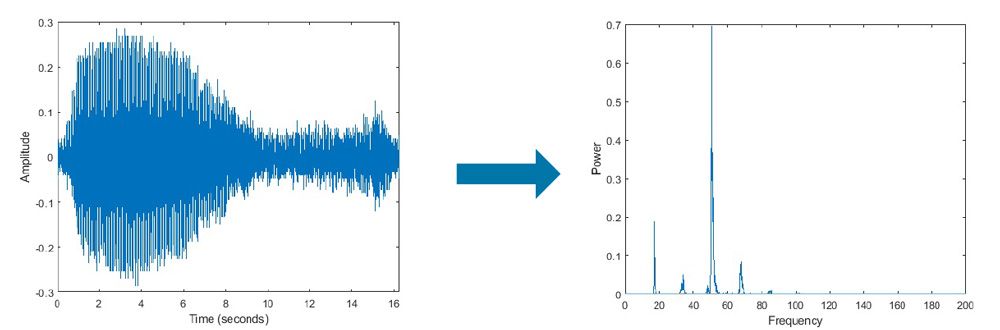
信号处理技术的目的是从信号中提取有用信息，包括滤波、傅里叶变换、小波变换等。MATLAB通过信号处理工具箱提供了一系列函数来进行这些操作。

% 使用傅里叶变换进行频谱分析
spectrum = fft(sineSignal);

通过本章的学习，读者应能够熟练使用MATLAB进行基本的信号处理操作，并为进一步深入学习参数估计和系统辨识打下坚实的基础。在后续章节中，我们将逐步探索这些高级主题，并着重介绍如何利用MATLAB实现复杂信号处理任务。

# 2. ```
# 第二章：参数估计的理论与方法

## 2.1 参数估计的基本概念

参数估计是统计学中的一个核心概念，它是指在一定的概率分布假设下，利用观测数据来推断总体参数的过程。参数估计的准确性直接影响到模型的性能，是数据分析中的重要环节。

### 2.1.1 参数估计的定义

参数估计通常可以分为两大类：点估计和区间估计。点估计是用一个统计量（如样本均值）来估计总体参数（如总体均值）。区间估计则是给出一个区间范围，这个区间以一定的概率包含未知的总体参数。

### 2.1.2 参数估计的目标与意义

参数估计的目标是通过有限的样本数据来尽可能准确地推断总体的特征，这在实际应用中有着广泛的意义。例如，在工程领域，参数估计可以帮助我们估计系统的可靠性；在金融领域，可以用来评估风险；在生物医学领域，可以用于疾病的预测和治疗效果的评估。

## 2.2 参数估计的主要方法

参数估计的方法众多，不同方法有各自的特点和适用范围。本章将介绍三种常见的参数估计方法：最小二乘法、极大似然估计和贝叶斯估计。

### 2.2.1 最小二乘法

最小二乘法是一种数学优化技术，通过最小化误差的平方和来寻找数据的最佳函数匹配。在最小二乘法中，目标是找到参数的估计值，使得观测数据与模型预测值之间的差的平方和最小。

#### 具体实现步骤：

1. 定义目标函数，通常为误差平方和。
2. 对目标函数关于未知参数求偏导，并令导数等于零。
3. 解方程组得到参数估计值。

#### 示例代码：

% 假设有一组数据点(x_data, y_data)和一个模型函数model_func
% model_func的参数是我们需要估计的
x_data = [...]; % 自变量数据
y_data = [...]; % 因变量数据
model_func = @(p, x) p(1)*exp(p(2)*x); % 模型函数，p为参数向量

% 使用MATLAB的fminsearch函数进行最小化计算
initial_params = [1, -1]; % 参数的初始猜测值
options = optimset('TolFun', 1e-6, 'MaxFunEvals', 10000, 'MaxIter', 10000); % 设置优化参数
best_params = fminsearch(@(p) sum((y_data - model_func(p, x_data)).^2), initial_params, options);

% 输出参数估计值
disp(best_params);

### 2.2.2 极大似然估计

极大似然估计是一种基于概率模型的参数估计方法，其核心思想是选择那些使得观测到的数据出现概率最大的参数值。

#### 实现步骤：

1. 定义似然函数，即给定参数下观测数据出现的概率。
2. 对似然函数取对数，得到对数似然函数。
3. 对对数似然函数关于参数求导，并令导数等于零。
4. 解方程得到参数的估计值。

#### 示例代码：

% 假设我们有一组数据y_data和正态分布的概率密度函数
n = length(y_data); % 数据点个数
mu = sum(y_data)/n; % 均值的估计
sigma_squared = sum((y_data - mu).^2)/n; % 方差的估计

% 输出极大似然估计得到的参数值
disp(mu);
disp(sigma_squared);

### 2.2.3 贝叶斯估计

贝叶斯估计是基于贝叶斯定理的一种参数估计方法，它考虑了参数的先验知识，结合观测数据来计算参数的后验分布。

#### 实现步骤：

1. 设定参数的先验分布。
2. 根据观测数据和先验分布计算后验分布。
3. 对后验分布进行分析，得到参数的估计值。

#### 示例代码：

% 假设参数theta的先验分布是beta分布，观测数据y服从二项分布
alpha_prior = 2; % beta分布的alpha参数
beta_prior = 2; % beta分布的beta参数
y = [1, 0, 1, 1, 0, 1, 0, 0]; % 观测数据

% 使用MATLAB的betafit函数进行贝叶斯估计
theta_posterior = betafit(y + alpha_prior, length(y) + beta_prior);
% 输出后验分布的参数估计值
disp(theta_posterior);

## 2.3 参数估计的性能分析

为了评价参数估计方法的好坏，通常会进行一致性和效率分析。

### 2.3.1 一致性分析

一致性分析是考察估计量是否随着样本量的增加而收敛于真实参数值。如果一个估计量是无偏的，并且随着样本量的增加，其方差趋于零，则称这个估计量是渐进一致的。

### 2.3.2 效率分析

效率分析主要是比较不同估计量的方差大小。一般而言，方差越小的估计量效率越高。Cramer-Rao不等式为评估参数估计的效率提供了一个理论下界。

#### 示例分析：

- 在实际应用中，可以通过模拟不同的样本量进行参数估计，然后分析估计量的偏差、方差随样本量变化的趋势，以此来评估参数估计的一致性和效率。
- 评估时还可以使用诸如均方误差（MSE）这样的综合性指标，它考虑了估计值偏离真实值的平方的期望，反映了估计的准确性和精确性。

参数估计的理论与方法是信号处理和数据分析中的重要工具。本章所介绍的方法和分析手段为深入理解和应用参数估计提供了基础。在后续章节中，我们将进一步探讨如何利用MATLAB来实现这些参数估计方法，并通过实际案例来加深对理论的理解。

# 3. 系统辨识的理论与实践

系统辨识是理解和建模动态系统的关键步骤，涉及从输入和输出数据中估计系统参数，以及建立这些参数的数学模型。本章将探讨系统辨识的基本框架和方法，并通过实例分析加深理解。

## 3.1 系统辨识的基本框架

### 3.1.1 系统辨识的定义和目的

系统辨识是一门涉及数学、统计学和计算机科学的交叉学科，它主要研究如何利用观测数据来建立或改善系统的数学模型。系统辨识的目的在于，通过观测数据来构建一个能够准确描述系统行为的模型，从而为系统分析、控制、预测等提供基础。

### 3.1.2 系统模型的选择与分类

系统模型的类型取决于辨识的目标和可用数据。常见的系统模型有：

- **离散时间模型和连续时间模型：** 基于时间属性的不同，系统可以建模为离散或连续。
- **线性模型和非线性模型：** 线性模型简单且易于分析，而非线性模型则能更准确地描述真实世界的复杂系统。
- **黑箱模型、灰箱模型和白箱模型：** 这三种模型分别对应不同水平的系统知识。黑箱模型不考虑系统内部结构，灰箱模型考虑部分内部信息，而白箱模型则对系统内部结构有详尽的了解。

## 3.2 系统辨识的常用算法

### 3.2.