【深入理解MATLAB频谱分析】：FFT和IFFT的奥秘

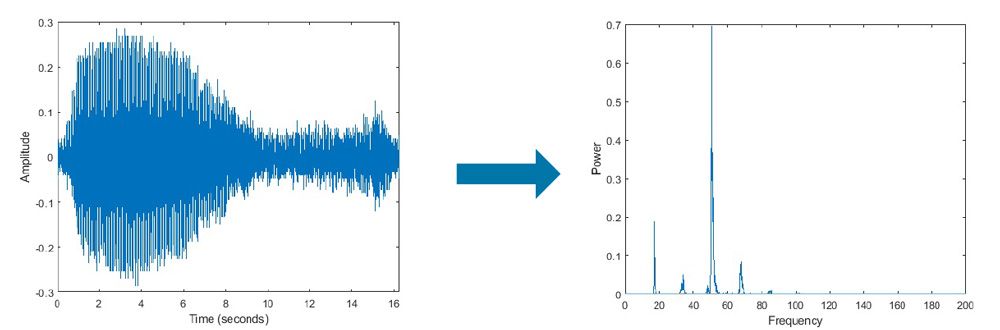
# 1. MATLAB频谱分析基础

频谱分析是数字信号处理中的核心内容，它允许我们从频域的角度理解信号的本质特征。在MATLAB环境中，频谱分析变得更为直观和高效，这得益于MATLAB强大的数值计算能力和丰富的内置函数库。

## 1.1 频谱分析的目的与意义

频谱分析的目的是从复杂的时域信号中提取频率成分，以识别信号的频域特性。这项技术广泛应用于音频处理、通信系统、生物医学信号分析等领域。通过频谱分析，工程师和科学家能够更好地理解信号的组成，从而进行有效的信号处理和分析。

## 1.2 MATLAB在频谱分析中的角色

MATLAB提供了一系列用于频谱分析的工具和函数，使得从信号采集、处理到可视化的过程变得简单而高效。MATLAB的频谱分析功能不仅支持基础的快速傅里叶变换（FFT），还包括窗函数技术、信号滤波等高级技术，支持用户快速实现从理论到实践的转换。

## 1.3 频谱分析的基本步骤

进行MATLAB频谱分析的基本步骤包括信号的采集、预处理（如滤波）、FFT变换、频谱的可视化，以及结果的分析和解释。这个过程不仅要求对MATLAB工具的熟练使用，更需要对信号处理理论的深刻理解。

% MATLAB代码示例：简单的FFT分析
% 假设我们有一个简单的正弦信号
Fs = 1000;            % 采样频率
t = 0:1/Fs:1-1/Fs;    % 时间向量
f = 5;                % 信号频率
signal = sin(2*pi*f*t); % 生成正弦信号

% 执行FFT变换
Y = fft(signal);
L = length(signal);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

% 定义频率域 f
f = Fs*(0:(L/2))/L;

% 绘制单边频谱
figure;
plot(f, P1);
title('Single-Sided Amplitude Spectrum of S(t)');
xlabel('f (Hz)');
ylabel('|P1(f)|');

通过以上代码，我们演示了如何利用MATLAB对简单正弦信号进行频谱分析。这仅仅是一个开始，MATLAB强大的分析能力可以支持更复杂的信号处理和分析任务。随着读者对频谱分析的深入理解和实践，可以探索MATLAB提供的更多高级功能来优化分析过程。

# 2. 快速傅里叶变换（FFT）的理论与实现

## 2.1 FFT算法的基本原理

### 2.1.1 离散傅里叶变换（DFT）的概念

离散傅里叶变换（Discrete Fourier Transform，DFT）是将时域的离散信号转换到频域的一种数学方法。DFT提供了一种观察信号频率成分的方式，它通过将时域信号表示成复指数函数的线性组合来工作。这一过程可以看作是对信号进行采样和重建的过程，将时域中的采样点通过正弦和余弦函数的叠加转换为频域中的频率成分。

在数学表达上，对于长度为N的复数序列 \(x[n]\)，其DFT定义为：

\[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j \frac{2\pi}{N}nk} \]

这里，\(X[k]\) 是复数序列 \(x[n]\) 在频率 \(k\) 处的频率分量，\(j\) 是虚数单位，\(e\) 是自然对数的底数。

### 2.1.2 FFT算法的数学推导

快速傅里叶变换（Fast Fourier Transform，FFT）是一种高效计算DFT的算法，由James W. Cooley和John W. Tukey在1965年提出。FFT显著减少了DFT的计算量，从原始算法的 \(O(N^2)\) 时间复杂度降低到 \(O(N \log N)\)。这一改进使得在实际中大规模的频谱分析成为可能。

FFT算法的核心思想是将原始的DFT问题分解为更小的DFT问题，并利用这些小问题的结果来构造原问题的解。分解通常利用一种称为“蝶形运算”的结构来实现。在递归分治的过程中，将原始的长度为N的DFT分解为两个长度为N/2的DFT，再将这两个DFT分解为四个长度为N/4的DFT，如此类推，直到分解为最简单的长度为1的DFT。

## 2.2 FFT在MATLAB中的应用

### 2.2.1 MATLAB内置FFT函数的使用方法

MATLAB提供了一个强大的内置函数`fft`，用于高效计算信号的快速傅里叶变换。使用`fft`函数非常简单，只需要将信号数据作为输入参数即可得到相应的频域表示。

例如，对于一个长度为N的信号向量x，计算其FFT只需要一行代码：

X = fft(x);

`fft`函数返回的是一个复数向量，其中包含了信号在不同频率上的分量的幅度和相位信息。要查看信号的幅度谱，可以使用`abs`函数取模；要查看信号的相位谱，可以使用`angle`函数取相位角。

### 2.2.2 优化FFT性能的策略

在实际应用中，FFT的性能可以通过多种策略来优化。首先，信号长度N通常选择为2的幂次，这样可以利用FFT算法的最佳性能。MATLAB在执行`fft`时会自动检测信号长度是否为最优化值，如果不是，会进行适当的填充（zero-padding）或截断。

另一个性能优化策略是并行计算。随着多核处理器的普及，MATLAB也提供了多线程支持，允许在计算FFT时并行处理多个数据块。这可以通过使用`parfor`循环来实现，并确保使用了`fft`的并行版本。

## 2.3 FFT分析的案例研究

### 2.3.1 音频信号的频谱分析

通过FFT对音频信号进行频谱分析是音频处理中的一个基本操作。以下是一个简单的案例研究，展示如何使用MATLAB的`fft`函数来分析音频信号的频谱。

% 读取音频文件
[x, Fs] = audioread('example.wav'); % x是音频数据，Fs是采样频率

% 计算FFT
X = fft(x);

% 计算频率向量
N = length(x);
f = (0:N-1)*(Fs/N);

% 绘制幅度谱
X_mag = abs(X);
X_mag = X_mag(1:N/2+1);
f = f(1:N/2+1);
figure;
plot(f, X_mag);
title('Audio Signal Spectrum');
xlabel('Frequency (Hz)');
ylabel('Magnitude');

在这个例子中，我们首先读取一个音频文件，然后计算其FFT，得到信号的频率分量。最后，我们绘制了信号的幅度谱，并通过图形直观地展示了音频信号的频率分布。

### 2.3.2 电力系统信号的频谱分析

在电力系统中，FFT被广泛用于分析电压和电流信号的频谱特性。这对于检测电网中的谐波失真、监控电力系统的稳定性等都有非常重要的作用。以下是一个简单的案例研究，展示如何使用MATLAB进行电力系统信号的FFT分析。

% 读取电力系统信号数据
load power_data.mat; % 假设数据文件包含电压或电流信号

% 计算FFT
X = fft(signal);

% 计算频率向量
Fs = sampleRate; % 假设采样频率已知
N = length(signal);
f = (0:N-1)*(Fs/N);

% 绘制幅度谱
X_mag = abs(X);
X_mag = X_mag(1:N/2+1);
f = f(1:N/2+1);
figure;
plot(f, X_mag);
title('Power System Signal Spectrum');
xlabel('Frequency (Hz)');
ylabel('Magnitude');

在这个例子中，我们加载了一个电力系统信号数据，并计算了其FFT，得到信号的频率分量。通过绘制信号的幅度谱，我们可以观察到电力系统中的频率成分，例如基波和谐波等。

以上案例展示了FFT在不同领域的应用，不仅限于信号处理，还包括音频分析、电力系统监控等。理解FFT的原理及其在MATLAB中的实现，为在这些领域的深入分析打下了坚实的基础。

# 3. 逆快速傅里叶变换（IFFT）的