排序算法实战指南：根据场景精准选择最佳算法

# 1. 排序算法概述

排序算法是计算机科学中一种基本算法，用于对数据集合中的元素进行重新排列，使其满足某种特定顺序。排序算法在各种应用场景中都至关重要，包括数据分析、数据库管理和机器学习。

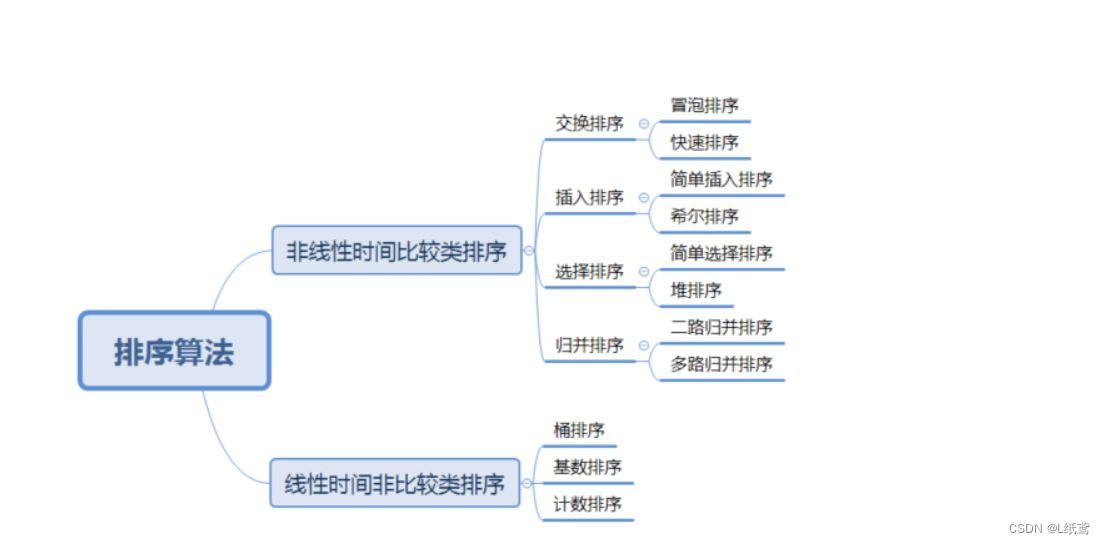
排序算法通常分为两大类：比较排序算法和非比较排序算法。比较排序算法通过比较元素之间的值来确定它们的顺序，而非比较排序算法则使用其他机制，例如哈希或计数。

# 2. 排序算法理论基础

### 2.1 比较排序算法

比较排序算法通过比较相邻元素之间的值来确定元素的顺序。比较排序算法的时间复杂度通常为 O(n^2)，其中 n 为待排序元素的数量。

#### 2.1.1 冒泡排序

冒泡排序通过不断比较相邻元素，将较大的元素向后移动，直到所有元素按升序排列。其算法流程如下：

def bubble_sort(arr):
    for i in range(len(arr) - 1):
        for j in range(len(arr) - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

**代码逻辑分析：**

* 外层循环 `for i in range(len(arr) - 1)` 遍历数组，表示需要进行的排序趟数。
* 内层循环 `for j in range(len(arr) - i - 1)` 遍历未排序的元素，比较相邻元素。
* 如果 `arr[j] > arr[j + 1]`，则交换这两个元素。

**参数说明：**

* `arr`：待排序的数组。

#### 2.1.2 选择排序

选择排序通过在未排序部分中找到最小（或最大）元素，然后将其与未排序部分的第一个元素交换，重复此过程直到所有元素按升序排列。其算法流程如下：

def selection_sort(arr):
    for i in range(len(arr)):
        min_idx = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

**代码逻辑分析：**

* 外层循环 `for i in range(len(arr))` 遍历数组，表示需要进行的排序趟数。
* 内层循环 `for j in range(i + 1, len(arr))` 遍历未排序的元素，寻找最小元素。
* 如果 `arr[j] < arr[min_idx]`，则更新最小元素索引 `min_idx`。
* 最后，交换 `arr[i]` 和 `arr[min_idx]`。

**参数说明：**

* `arr`：待排序的数组。

#### 2.1.3 插入排序

插入排序通过将未排序元素插入到已排序部分的正确位置，重复此过程直到所有元素按升序排列。其算法流程如下：

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key

**代码逻辑分析：**

* 外层循环 `for i in range(1, len(arr))` 遍历未排序的元素。
* 将 `arr[i]` 作为待插入元素 `key`。
* 内层循环 `while j >= 0 and key < arr[j]` 查找 `key` 在已排序部分中的正确位置。
* 将已排序部分中的元素向后移动，为 `key` 腾出位置。
* 最后，将 `key` 插入到正确位置。

**参数说明：**

* `arr`：待排序的数组。

# 3.1 数据结构对排序算法的影响

数据结构的选择会对排序算法的性能产生显著影响。不同的数据结构具有不同的特性，这些特性会影响算法的执行效率。

#### 3.1.1 数组

数组是一种顺序存储结构，元素在内存中连续存储。数组的优势在于其快速的数据访问和索引能力。对于基于比较的排序算法，如冒泡排序、选择排序和插入排序，数组的顺序存储特性使其能够高效地比较相邻元素。

def bubble_sort(arr):
    """
    冒泡排序算法

    参数：
        arr: 待排序数组

    逻辑分析：
        冒泡排序通过不断比较相邻元素并交换位置，将最大元素逐步移动到数组末尾。

    时间复杂度：O(n^2)
    空间复杂度：O(1)
    """
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

#### 3.1.2 链表

链表是一种动态存储结构，元素通过指针连接。链表的优势在于其插入和删除操作的效率。对于基于交换的排序算法，如快速排序和归并排序，链表的动态存储特性使其能够灵活地移动元素，从而实现高效的排序。

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

def merge_sort(head):
    """
    归并排序算法

    参数：
        head: 待排序链表的头节点

    逻辑分析：
        归并排序采用分治思想，将链表拆分成多个子链表，分别排序后合并。

    时间复杂度：O(n log n)
    空间复杂度：O(n)
    """
    if not head or not head.next:
        return head

    mid = get_middle(head)
    right_half = mid.next
    mid.next = None

    left_half = merge_sort(head)
    right_half = merge_sort(right_half)

    return merge_two_sorted_lists(left_half, right_half)

#### 3.1.3 哈希表

哈希表是一种基于键值对存储的结构。哈希表的优势在于其快速的数据查找和插入能力。对于基于比较的排序算法，哈希表可以通过将元素映射到不同的桶中来实现快速排序。

import hashlib

def hash_sort(arr):
    """
    哈希排序算法

    参数：
        arr: 待排序数组

    逻辑分析：
        哈希排序利用哈希表将元素映射到不同的桶中，然后对每个桶中的元素进行排序。

    时间复杂度：O(n)
    空间复杂度：O(n)
    """
    hash_table = {}

    for element in arr:
        hash_key = hashlib.md5(str(element).encode()).hexdigest()
        if hash_key not in hash_table:
            hash_table[hash_key] = []
        hash_table[hash_key].append(element)

    sorted_arr = []
    for key in hash_table:
        sorted_arr.extend(sorted(hash_table[key]))

    return sorted_arr

# 4. 排序算法优化技巧

排序算法的优化技巧主要从时间复杂度和空间复杂度两个方面进行。

### 4.1 时间复杂度优化

#### 4.1.1 剪枝优化

剪枝优化是一种通过提前判断元素是否满足排序条件，从而减少不必要的比较和交换操作的优化技巧。例如，在冒泡排序中，当发现某一轮排序后没有发生任何交换时，说明数组已经有序，此时可以提前终止排序。

#### 4.1.2 分治优化

分治优化是一种将大问题分解成若干个小问题的优化技巧。例如，归并排序和快速排序都是采用分治的思想，将待排序数组不断分解成较小的子数组，分别进行排序，然后再合并成有序的数组。

#### 4.1.3 桶排序

桶排序是一种非比较排序算法，其时间复杂度为 O(n+k)，其中 n 为待排序元素个数，k 为桶的个数。桶排序的原理是将待排序元素分配到不同的桶中，每个桶内再进行排序，最后将各个桶内的元素合并成有序的数组。

### 4.2 空间复杂度优化

#### 4.2.1 归并排序的非递归实现

归并排序的递归实现需要额外的空间存储临时数组。通过使用迭代的方式代替递归，可以避免使用额外的空间。

#### 4.2.2 快速排序的尾递归优化

快速排序的递归实现也需要额外的空间存储递归栈。通过使用尾递归优化，可以将递归栈的空间复杂度降为 O(1)。

#### 4.2.3 堆排序的原地排序

堆排序是一种原地排序算法，不需要额外的空间存储临时数组。堆排序的原理是将待排序数组构建成一个大根堆，然后依次弹出堆顶元素，得到有序的数组。

### 代码示例

#### 剪枝优化（冒泡排序）

def bubble_sort_with_pruning(arr):
    """
    冒泡排序优化：当某一轮排序后没有发生任何交换时，说明数组已经有序，提前终止排序。

    Args:
        arr: 待排序数组

    Returns:
        排序后的数组
    """
    n = len(arr)
    for i in range(n):
        swapped = False
        for j in range(n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                swapped = True
        if not swapped:
            break
    return arr

#### 分治优化（归并排序）

def merge_sort(arr):
    """
    归并排序：采用分治思想，将大问题分解成若干个小问题，分别进行排序，然后再合并成有序的数组。

    Args:
        arr: 待排序数组

    Returns:
        排序后的数组
    """
    n = len(arr)
    if n <= 1:
        return arr

    mid = n // 2
    left_half = merge_sort(arr[:mid])
    right_half = merge_sort(arr[mid:])

    return merge(left_half, right_half)

def merge(left, right):
    """
    合并两个有序数组

    Args:
        left: 左侧有序数组
        right: 右侧有序数组

    Returns:
        合并后的有序数组
    """
    i = 0
    j = 0
    merged = []
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            merged.append(left[i])
            i += 1
        else:
            merged.append(right[j])
            j += 1

    while i < len(left):
        merged.append(left[i])
        i += 1

    while j < len(right):
        merged.append(right[j])
        j += 1

    return merged

#### 桶排序

def bucket_sort(arr, k):
    """
    桶排序：将待排序元素分配到不同的桶中，每个桶内再进行排序，最后将各个桶内的元素合并成有序的数组。

    Args:
        arr: 待排序数组
        k: 桶的个数

    Returns:
        排序后的数组
    """
    n = len(arr)
    buckets = [[] for _ in range(k)]

    # 将元素分配到不同的桶中
    for i in range(n):
        bucket_index = int(arr[i] * (k - 1))
        buckets[bucket_index].append(arr[i])

    # 对每个桶内的元素进行排序
    for bucket in buckets:
        bucket.sort()

    # 将各个桶内的元素合并成有序的数组
    sorted_arr = []
    for bucket in buckets:
        sorted_arr.extend(bucket)

    return sorted_arr

# 5.1 分布式排序

在处理大规模数据集时，传统的排序算法可能会遇到内存和计算资源的限制。分布式排序技术通过将排序任务分布在多个节点上，有效地解决了这些问题。

### 5.1.1 MapReduce 框架

MapReduce 是一个分布式计算框架，它将数据处理任务分解为两个阶段：

- **Map 阶段：**将输入数据拆分成较小的块，并应用一个映射函数对每个块进行处理，产生键值对。
- **Reduce 阶段：**将相同键的键值对聚合在一起，应用一个规约函数对聚合后的数据进行进一步处理。

**排序应用：**

使用 MapReduce 进行排序时，Map 阶段将输入数据拆分成块，并对每个块应用一个映射函数，将每个元素映射为键值对，其中键是元素本身，值是 1。Reduce 阶段将相同元素的键值对聚合在一起，并应用一个规约函数对聚合后的数据进行排序。

### 5.1.2 Spark 框架

Spark 是一个统一的分布式计算引擎，它提供了更高级别的 API，简化了分布式应用程序的开发。Spark 支持多种排序算法，包括：

- **排序ByKey：**对键进行排序，并返回键值对。
- **sortBy：**根据指定的函数对元素进行排序，并返回排序后的元素。

**排序应用：**

使用 Spark 进行排序时，可以使用 `sortBy` 函数对元素进行排序。以下代码示例演示了如何使用 Spark 对一个 RDD 进行排序：

import org.apache.spark.rdd.RDD

val rdd: RDD[Int] = ...

// 对 RDD 中的元素进行升序排序
val sortedRDD: RDD[Int] = rdd.sortBy(x => x)

// 对 RDD 中的元素进行降序排序
val sortedRDD: RDD[Int] = rdd.sortBy(x => -x)