排序函数实现大全：从基础到优化，手把手教你写出高效代码

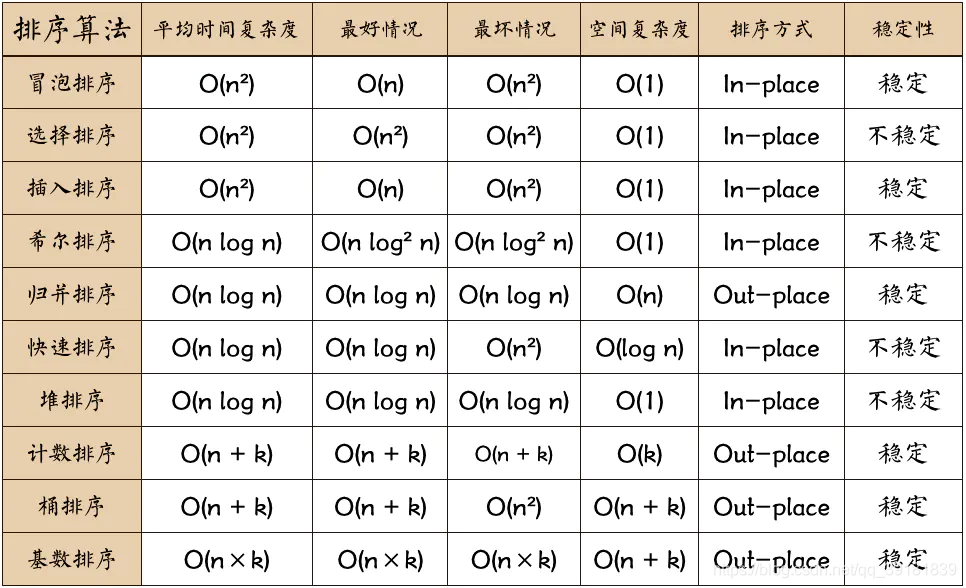
# 1. 排序算法基础**

排序算法是计算机科学中用于对数据进行排列的一种算法。排序算法的基本思想是将数据按照一定的顺序排列，例如升序或降序。排序算法广泛应用于各种领域，例如数据库管理、数据分析和机器学习。

排序算法的性能由时间复杂度和空间复杂度决定。时间复杂度衡量算法执行所需的时间，而空间复杂度衡量算法执行所需的空间。常见的排序算法包括冒泡排序、选择排序和插入排序，这些算法的时间复杂度为 O(n^2)，其中 n 是数据元素的数量。

# 2. 经典排序算法

经典排序算法是排序算法的基础，它们简单易懂，在各种场景下都有广泛的应用。本章将介绍三种经典排序算法：冒泡排序、选择排序和插入排序。

### 2.1 冒泡排序

冒泡排序是一种简单的排序算法，它通过不断比较相邻元素，将较大的元素向后移动，直到所有元素按升序排列。

**算法步骤：**

1. 遍历数组，比较相邻元素。
2. 如果前一个元素大于后一个元素，则交换它们。
3. 重复步骤 1 和 2，直到数组完全排序。

**代码实现：**

def bubble_sort(arr):
    """
    冒泡排序算法

    Args:
        arr (list): 待排序数组

    Returns:
        list: 排序后的数组
    """
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr

**逻辑分析：**

* 外层循环 `for i in range(n)` 遍历数组，每轮将最大的元素移动到末尾。
* 内层循环 `for j in range(0, n - i - 1)` 比较相邻元素并交换。
* 随着外层循环的进行，已排序元素逐渐增加，内层循环的范围缩小。

### 2.2 选择排序

选择排序是一种基于选择思想的排序算法，它通过不断选择数组中最小元素，将其与当前元素交换，直到所有元素按升序排列。

**算法步骤：**

1. 遍历数组，找到最小元素。
2. 将最小元素与当前元素交换。
3. 重复步骤 1 和 2，直到数组完全排序。

**代码实现：**

def selection_sort(arr):
    """
    选择排序算法

    Args:
        arr (list): 待排序数组

    Returns:
        list: 排序后的数组
    """
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i + 1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
    return arr

**逻辑分析：**

* 外层循环 `for i in range(n)` 遍历数组，每轮将最小元素移动到当前位置。
* 内层循环 `for j in range(i + 1, n)` 寻找当前元素后的最小元素。
* 找到最小元素后，将其与当前元素交换。

### 2.3 插入排序

插入排序是一种基于插入思想的排序算法，它通过将当前元素插入到前面已排序的序列中，直到所有元素按升序排列。

**算法步骤：**

1. 遍历数组，从第二个元素开始。
2. 将当前元素与前面已排序序列中的元素比较。
3. 找到合适的位置，将当前元素插入。
4. 重复步骤 2 和 3，直到数组完全排序。

**代码实现：**

def insertion_sort(arr):
    """
    插入排序算法

    Args:
        arr (list): 待排序数组

    Returns:
        list: 排序后的数组
    """
    n = len(arr)
    for i in range(1, n):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

**逻辑分析：**

* 外层循环 `for i in range(1, n)` 遍历数组，从第二个元素开始。
* 内层循环 `while j >= 0 and key < arr[j]` 寻找合适的位置插入当前元素。
* 找到合适的位置后，将已排序序列中的元素向后移动，腾出空间插入当前元素。

# 3.1 快速排序

快速排序是一种分治排序算法，它将数组划分为两个较小的子数组，然后递归地对每个子数组进行排序。快速排序的平均时间复杂度为 O(n log n)，最坏情况下的时间复杂度为 O(n^2)。

#### 算法流程

快速排序的算法流程如下：

1. 选择一个基准元素。
2. 将数组划分为两个子数组：小于基准元素的元素和大于基准元素的元素。
3. 递归地对两个子数组进行排序。

#### 代码实现

def quick_sort(arr):
    """快速排序算法

    Args:
        arr: 待排序的数组

    Returns:
        排序后的数组
    """

    if len(arr) <= 1:
        return arr

    # 选择基准元素
    pivot = arr[len(arr) // 2]

    # 划分数组
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]

    # 递归地对子数组进行排序
    return quick_sort(left) + middle + quick_sort(right)

#### 逻辑分析

快速排序的逻辑分析如下：

1. **选择基准元素：**基准元素的选择对快速排序的性能有很大的影响。如果基准元素选择得不好，可能会导致最坏情况下的时间复杂度 O(n^2)。
2. **划分数组：**划分数组可以采用多种方法，例如双指针法或荷兰国旗问题算法。
3. **递归排序：**递归排序子数组是快速排序的关键步骤。递归深度与数组的大小成正比，因此平均时间复杂度为 O(n log n)。

#### 参数说明

* **arr：**待排序的数组

#### 代码解读

# 选择基准元素
pivot = arr[len(arr) // 2]

这行代码选择数组中间元素作为基准元素。

# 划分数组
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]

这三行代码使用列表解析划分数组。

# 递归地对子数组进行排序
return quick_sort(left) + middle + quick_sort(right)

这行代码递归地对子数组进行排序，并返回排序后的数组。

# 4. 排序算法优化

### 4.1 时间复杂度分析

排序算法的时间复杂度是衡量算法效率的重要指标。它表示算法在最坏情况下执行所需的时间。常见的排序算法时间复杂度如下：

| 排序算法 | 时间复杂度 |
|---|---|
| 冒泡排序 | O(n^2) |
| 选择排序 | O(n^2) |
| 插入排序 | O(n^2) |
| 快速排序 | O(n log n) |
| 归并排序 | O(n log n) |
| 堆排序 | O(n log n) |

时间复杂度分析可以帮助我们选择在给定数据集上使用最合适的排序算法。例如，对于较小的数据集，冒泡排序或选择排序可能就足够了。对于较大的数据集，快速排序或归并排序是更好的选择。

### 4.2 空间复杂度优化

空间复杂度表示算法在执行过程中所需的内存量。与时间复杂度类似，空间复杂度也是衡量算法效率的重要指标。

常见的排序算法空间复杂度如下：

| 排序算法 | 空间复杂度 |
|---|---|
| 冒泡排序 | O(1) |
| 选择排序 | O(1) |
| 插入排序 | O(1) |
| 快速排序 | O(log n) |
| 归并排序 | O(n) |
| 堆排序 | O(1) |

空间复杂度优化可以帮助我们选择在内存受限的环境中使用最合适的排序算法。例如，如果内存有限，冒泡排序、选择排序或插入排序是不错的选择。

### 4.3 稳定性与不稳定性

稳定性是排序算法的一个重要特性。它表示算法是否保持相等元素的相对顺序。

**稳定排序算法**：在排序过程中保持相等元素的相对顺序。
**不稳定排序算法**：在排序过程中可能改变相等元素的相对顺序。

常见的排序算法稳定性如下：

| 排序算法 | 稳定性 |
|---|---|
| 冒泡排序 | 稳定 |
| 选择排序 | 不稳定 |
| 插入排序 | 稳定 |
| 快速排序 | 不稳定 |
| 归并排序 | 稳定 |
| 堆排序 | 不稳定 |

稳定性在某些情况下很重要。例如，如果我们有一个包含学生成绩和姓名的数据集，并且我们想按成绩对数据集进行排序，同时保持同等成绩的学生按姓氏的顺序，那么我们应该使用稳定的排序算法，如冒泡排序或归并排序。

# 5.1 Python中的排序算法

Python提供了丰富的内置函数和第三方库来实现各种排序算法。

### 内置函数

Python内置的`sort()`方法可以对可迭代对象（如列表、元组）进行排序。它使用快速排序算法，时间复杂度为O(n log n)。

# 对列表进行升序排序
my_list = [5, 2, 8, 3, 1]
my_list.sort()
print(my_list)  # 输出：[1, 2, 3, 5, 8]

# 对元组进行降序排序
my_tuple = (5, 2, 8, 3, 1)
my_tuple = sorted(my_tuple, reverse=True)
print(my_tuple)  # 输出：[8, 5, 3, 2, 1]

### 第三方库

Python生态系统中提供了许多第三方库，提供了更高级的排序算法和优化。

**NumPy**

NumPy库提供了`np.sort()`函数，它使用快速排序算法对NumPy数组进行排序。它还提供了`np.argsort()`函数，返回排序后的数组的索引。

import numpy as np

# 对NumPy数组进行升序排序
my_array = np.array([5, 2, 8, 3, 1])
my_array = np.sort(my_array)
print(my_array)  # 输出：[1, 2, 3, 5, 8]

# 获取排序后的索引
my_indices = np.argsort(my_array)
print(my_indices)  # 输出：[0, 1, 2, 3, 4]

**SciPy**

SciPy库提供了`scipy.sort()`函数，它支持多种排序算法，包括快速排序、归并排序和堆排序。

from scipy.sort import quicksort, mergesort, heapsort

# 使用快速排序对列表进行升序排序
my_list = [5, 2, 8, 3, 1]
quicksort(my_list)
print(my_list)  # 输出：[1, 2, 3, 5, 8]

# 使用归并排序对元组进行降序排序
my_tuple = (5, 2, 8, 3, 1)
mergesort(my_tuple, axis=0, order='descending')
print(my_tuple)  # 输出：[8, 5, 3, 2, 1]

### 选择排序算法

在Python中，可以使用以下代码实现选择排序算法：

def selection_sort(arr):
    """
    选择排序算法

    参数：
        arr: 待排序的列表

    返回：
        排序后的列表
    """

    # 遍历列表
    for i in range(len(arr)):
        # 找到当前元素之后的最小元素的索引
        min_idx = i
        for j in range(i+1, len(arr)):
            if arr[j] < arr[min_idx]:
                min_idx = j

        # 交换当前元素和最小元素
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

    return arr

**代码逻辑分析：**

* 外层循环`for i in range(len(arr))`遍历列表中的每个元素。
* 内层循环`for j in range(i+1, len(arr))`查找当前元素之后的最小元素。
* 如果找到更小的元素，则更新`min_idx`为该元素的索引。
* 最后，交换当前元素和最小元素的位置。

**参数说明：**

* `arr`: 待排序的列表。

**返回说明：**

* 返回排序后的列表。

# 6. 高级排序算法**

**6.1 计数排序**

计数排序是一种非比较排序算法，适用于输入数据范围有限且分布均匀的情况。其基本原理是：

1. 统计输入数组中每个元素出现的次数。
2. 根据统计结果，计算每个元素在排序后数组中的位置。
3. 根据位置信息，将元素依次写入排序后数组。

**代码实现：**

def counting_sort(arr):
    """
    计数排序算法

    :param arr: 输入数组
    :return: 排序后的数组
    """
    max_value = max(arr)
    min_value = min(arr)
    count_arr = [0] * (max_value - min_value + 1)  # 统计数组

    # 统计每个元素出现的次数
    for i in arr:
        count_arr[i - min_value] += 1

    # 计算每个元素在排序后数组中的位置
    for i in range(1, len(count_arr)):
        count_arr[i] += count_arr[i - 1]

    # 将元素依次写入排序后数组
    sorted_arr = [0] * len(arr)
    for i in range(len(arr) - 1, -1, -1):
        sorted_arr[count_arr[arr[i] - min_value] - 1] = arr[i]
        count_arr[arr[i] - min_value] -= 1

    return sorted_arr

**6.2 桶排序**

桶排序是一种非比较排序算法，适用于输入数据分布范围较大的情况。其基本原理是：

1. 将输入数组划分为多个大小相等的桶。
2. 将输入元素分配到相应的桶中。
3. 对每个桶内的元素进行排序。
4. 将各个桶内排序后的元素合并为排序后的数组。

**代码实现：**

def bucket_sort(arr, bucket_size):
    """
    桶排序算法

    :param arr: 输入数组
    :param bucket_size: 桶大小
    :return: 排序后的数组
    """
    max_value = max(arr)
    min_value = min(arr)
    num_buckets = (max_value - min_value) // bucket_size + 1  # 桶数量

    # 创建桶
    buckets = [[] for _ in range(num_buckets)]

    # 将元素分配到桶中
    for i in arr:
        buckets[(i - min_value) // bucket_size].append(i)

    # 对每个桶内的元素进行排序
    for bucket in buckets:
        bucket.sort()

    # 将各个桶内排序后的元素合并
    sorted_arr = []
    for bucket in buckets:
        sorted_arr.extend(bucket)

    return sorted_arr

**6.3 基数排序**

基数排序是一种非比较排序算法，适用于输入数据为整数且范围有限的情况。其基本原理是：

1. 从最低位开始，逐位比较和排序。
2. 对每一数位，使用计数排序或桶排序。
3. 重复步骤1和2，直到所有数位排序完成。

**代码实现：**

def radix_sort(arr):
    """
    基数排序算法

    :param arr: 输入数组
    :return: 排序后的数组
    """
    max_value = max(arr)
    exp = 1
    while max_value // exp > 0:
        counting_sort(arr, exp)
        exp *= 10  # 逐位比较，移动一位