排序算法的无限可能：从数据分析到机器学习，解锁更多应用场景

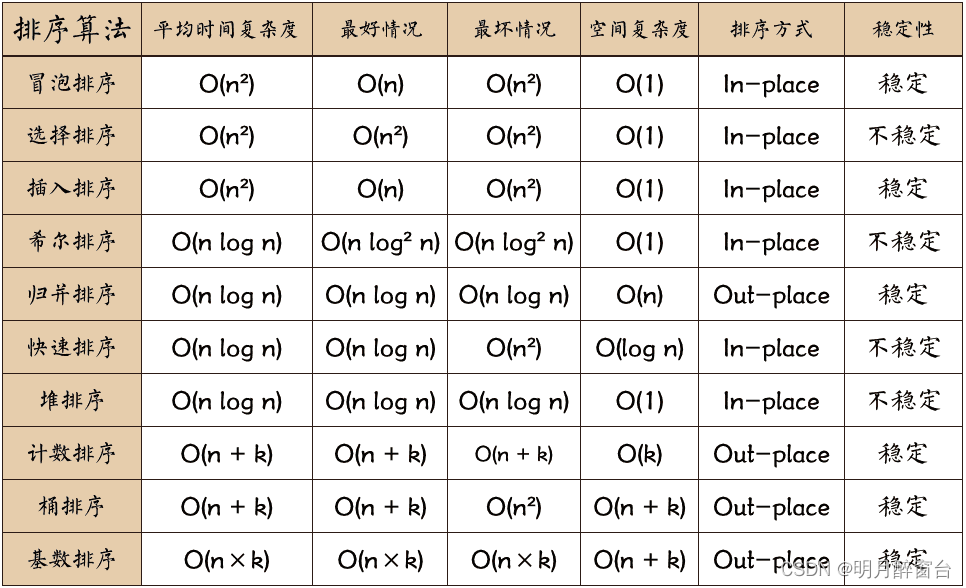
# 1. 排序算法概述

排序算法是一种计算机科学中的基本技术，用于将一组数据按特定顺序排列。排序算法广泛应用于各种领域，例如数据分析、机器学习和数据库管理。

排序算法的基本原理是比较两个元素并根据比较结果将它们交换位置。通过多次比较和交换，算法最终将数据排列成所需的顺序。不同的排序算法采用不同的比较策略和数据结构，从而产生不同的时间和空间复杂度。

排序算法的复杂度分析是评估算法效率的关键因素。时间复杂度衡量算法执行所需的时间，而空间复杂度衡量算法执行所需的空间。理解排序算法的复杂度对于选择最适合特定任务的算法至关重要。

# 2. 排序算法理论基础

### 2.1 排序算法的分类与特点

排序算法可以根据其工作原理分为两大类：比较排序算法和非比较排序算法。

#### 2.1.1 比较排序算法

比较排序算法通过比较元素之间的关系来确定它们的顺序。常见的比较排序算法包括：

- **冒泡排序：**逐个比较相邻元素，将较大的元素向后移动。
- **选择排序：**在未排序部分中找到最小元素，并将其与未排序部分的第一个元素交换。
- **插入排序：**将元素插入到已排序部分的正确位置。
- **快速排序：**使用分治法将数组划分为较小部分，并递归地对每个部分进行排序。
- **归并排序：**将数组分成两部分，分别排序，然后合并排序后的部分。

#### 2.1.2 非比较排序算法

非比较排序算法不通过比较元素之间的关系来确定它们的顺序。它们通常基于元素的分布或其他特性。常见的非比较排序算法包括：

- **计数排序：**根据元素的范围对元素进行计数，然后根据计数信息确定元素的顺序。
- **桶排序：**将元素分配到多个桶中，然后对每个桶中的元素进行排序。
- **基数排序：**将元素根据其各个位进行排序，从最低位到最高位。

### 2.2 排序算法的复杂度分析

排序算法的复杂度通常用时间复杂度和空间复杂度来衡量。

#### 2.2.1 时间复杂度

时间复杂度表示算法执行所需的时间。常见的排序算法的时间复杂度如下：

| 算法 | 最佳情况 | 平均情况 | 最坏情况 |
|---|---|---|---|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) |
| 插入排序 | O(n) | O(n^2) | O(n^2) |
| 快速排序 | O(n log n) | O(n log n) | O(n^2) |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) |

#### 2.2.2 空间复杂度

空间复杂度表示算法执行所需的内存空间。常见的排序算法的空间复杂度如下：

| 算法 | 空间复杂度 |
|---|---|
| 冒泡排序 | O(1) |
| 选择排序 | O(1) |
| 插入排序 | O(1) |
| 快速排序 | O(log n) |
| 归并排序 | O(n) |

**代码块：**

def bubble_sort(arr):
    """
    冒泡排序算法

    参数：
        arr: 待排序数组

    返回：
        排序后的数组
    """

    for i in range(len(arr) - 1):
        for j in range(len(arr) - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

    return arr

**逻辑分析：**

冒泡排序算法逐个比较相邻元素，将较大的元素向后移动。外层循环控制排序的次数，内层循环控制每次比较的元素对。如果相邻元素的顺序不正确，则交换它们的顺序。

**参数说明：**

* `arr`: 待排序的数组

# 3.1 排序算法在数据分析中的应用

排序算法在数据分析中扮演着至关重要的角色，它为数据预处理、清洗、探索和可视化奠定了基础。

#### 3.1.1 数据预处理和清洗

在数据分析过程中，数据预处理和清洗是必不可少的一步。排序算法可以帮助我们对数据进行排序，从而识别异常值、重复项和缺失值。

**代码示例：**

import numpy as np

# 生成一个包含异常值和重复项的数据集
data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3])

# 使用排序算法对数据进行排序
sorted_dat