排序函数常见错误大全：避开陷阱，编写高效代码

# 1. 排序算法的理论基础**

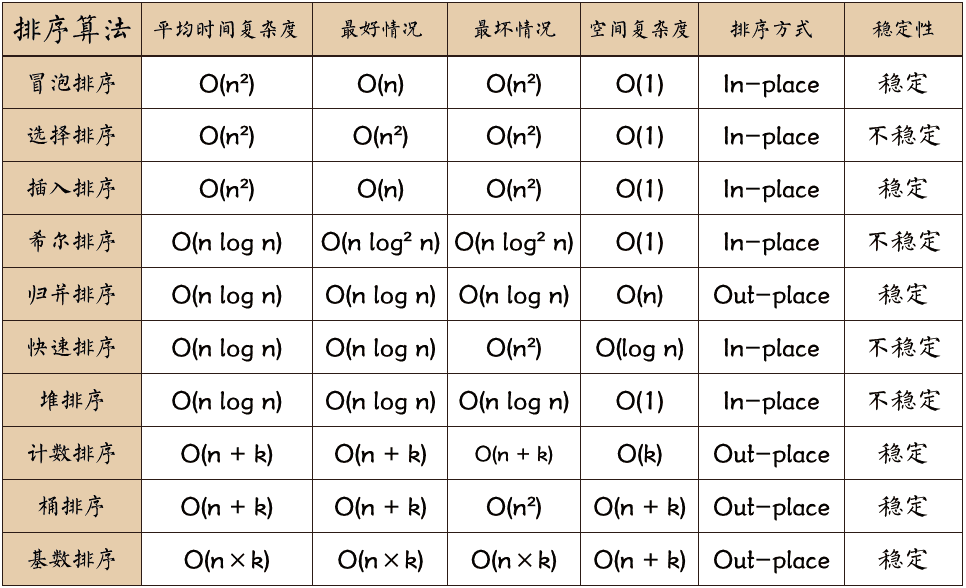
排序算法是计算机科学中用于对数据进行排序的基本算法。排序算法的目的是将数据按特定顺序排列，通常是升序或降序。

排序算法的效率由其时间复杂度和空间复杂度决定。时间复杂度衡量算法执行所需的时间，而空间复杂度衡量算法执行所需的内存量。

常见的排序算法包括冒泡排序、选择排序、插入排序、归并排序和快速排序。每种算法都有其独特的优点和缺点，具体选择取决于数据类型、数据量和所需的排序速度。

# 2. 排序函数常见的错误

排序函数在实际应用中经常会遇到各种各样的错误，这些错误不仅会影响排序结果的正确性，还会降低排序效率。本章将重点介绍排序函数中常见的错误，包括算法选择错误、数据类型处理不当等，并提供相应的解决方案。

### 2.1 算法选择错误

算法选择错误是排序函数中常见的错误之一。不同的排序算法具有不同的时间复杂度和稳定性，在不同的应用场景下，需要选择合适的排序算法。

#### 2.1.1 复杂度分析

排序算法的时间复杂度是衡量算法效率的重要指标。对于大规模数据集，选择时间复杂度较低的算法至关重要。

例如，对于一个包含 n 个元素的数组，冒泡排序的时间复杂度为 O(n^2)，而快速排序的时间复杂度为 O(n log n)。当 n 较小时，冒泡排序的效率可能高于快速排序，但当 n 较大时，快速排序的效率将明显高于冒泡排序。

#### 2.1.2 稳定性与否

稳定性是指排序算法在遇到相同元素时，保持其相对顺序不变。对于某些应用场景，稳定性至关重要。

例如，对于一个包含学生成绩的数组，如果使用不稳定的排序算法，可能会导致成绩相同的学生在排序后顺序发生改变，这将影响成绩排名。

### 2.2 数据类型处理不当

数据类型处理不当也是排序函数中常见的错误。排序算法需要根据数据类型进行比较和交换，如果数据类型处理不当，可能会导致排序结果不正确。

#### 2.2.1 比较函数的定义

比较函数是排序算法中用于比较两个元素的关键函数。如果比较函数定义不当，可能会导致排序结果不正确。

例如，对于一个包含字符串的数组，如果比较函数使用的是 ASCII 码比较，则会将大小写字母视为相等，导致排序结果不正确。

#### 2.2.2 数据类型转换

在某些情况下，需要对数据类型进行转换才能进行比较。如果数据类型转换不当，可能会导致比较结果不正确。

例如，对于一个包含整数和浮点数的数组，如果在比较前没有将整数转换为浮点数，则整数和浮点数将无法正确比较，导致排序结果不正确。

# 3. 排序函数的实践优化

### 3.1 优化算法实现

#### 3.1.1 减少比较次数

**优化策略：**

* **使用快速排序：**快速排序是一种分治算法，平均复杂度为 O(n log n)，比冒泡排序、选择排序等算法效率更高。
* **使用归并排序：**归并排序也是一种分治算法，平均复杂度为 O(n log n)，并且是稳定的排序算法。
* **使用桶排序：**桶排序适用于数据范围较小的情况，通过将数据分配到不同的桶中，可以减少比较次数。

**代码示例：**

def quick_sort(arr):
    if len(arr) <= 1:
        return arr

    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]

    return quick_sort(left) + middle + quick_sort(right)

**逻辑分析：**

快速排序将数组分成三部分：比枢纽小的元素、等于枢纽的元素和比枢纽大的元素。然后递归地对较小和较大的部分进行排序，最后合并三个部分。

#### 3.1.2 优化数据结构

**优化策略：**

* **使用数组而不是链表：**数组的随机访问性能优于链表，在排序操作中可以显著提高效率。
* **使用平衡树：**平衡树（如红黑树）可以保持数据有序，并支持高效的插入、删除和查找操作，从而优化排序过程。

**代码示例：**

import bisect

def binary_search_insert(arr, element):
    i = bisect.bisect_left(arr, element)
    arr.insert(i, element)

**逻辑分析：**

bisect_left 函数使用二分查找算法找到元素的插入位置，然后使用 insert 方法将元素插入到数组中。这种方法比线性搜索和插入效率更高。

### 3.2 提升代码效率

#### 3.2.1 内存管理

**优化策略：**

* **避免不必要的内存分配：**在排序