Trie树的性能优化技巧：提升搜索和插入效率（Trie树性能优化秘诀：提升搜索和插入效率）

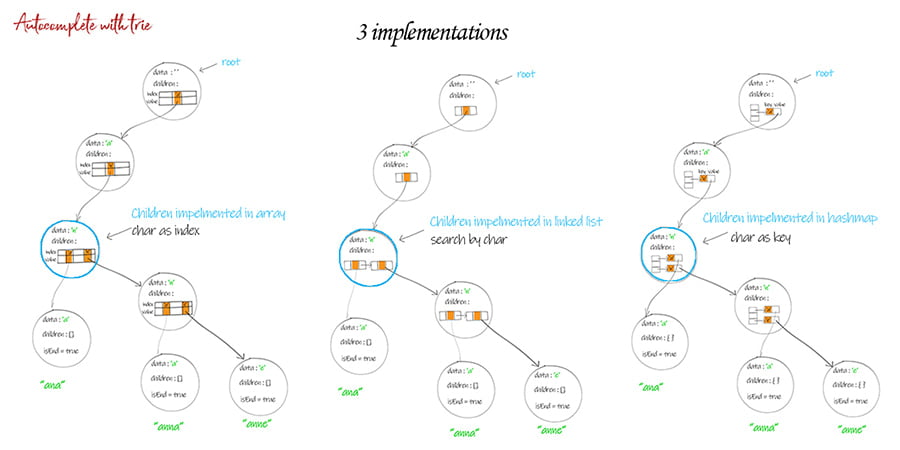
# 1. Trie树概述

Trie树，又称前缀树或字典树，是一种高效的数据结构，用于存储字符串集合并支持快速搜索和插入操作。它以树形结构组织字符串，其中每个节点代表字符串中的一个字符。

Trie树的优势在于其空间复杂度低，因为每个字符串只存储一次。此外，由于其树形结构，搜索和插入操作的时间复杂度为 O(m)，其中 m 是字符串的长度。这使得 Trie树在处理大量字符串时非常高效。

# 2. Trie树的性能瓶颈

### 2.1 节点膨胀

#### 2.1.1 原因分析

Trie树的节点膨胀问题主要源于以下原因：

- **大量重复前缀：**当插入大量具有相同前缀的字符串时，Trie树会创建大量的重复节点，导致空间浪费。
- **冗余空节点：**Trie树中可能存在大量空节点，这些节点不存储任何字符，但为了保持树的结构而存在。

#### 2.1.2 解决方法

解决节点膨胀问题的方法包括：

- **节点压缩：**将具有相同前缀的节点合并为一个节点，减少重复节点的数量。
- **分支剪枝：**删除不包含任何字符串的空分支，释放空间。

### 2.2 搜索效率低下

#### 2.2.1 原因分析

Trie树的搜索效率低下可能是由于以下原因：

- **树的高度过高：**当Trie树包含大量字符串时，树的高度可能会过高，导致搜索路径过长。
- **节点比较开销：**在搜索过程中，需要逐个比较节点中的字符，这会消耗大量时间。

#### 2.2.2 解决方法

提高搜索效率的方法包括：

- **分叉剪枝：**在搜索过程中，当遇到不包含目标字符串前缀的分支时，可以立即剪枝，避免不必要的搜索。
- **缓存机制：**缓存搜索结果，减少重复搜索的开销。

# 3. Trie树性能优化实践

### 3.1 节点压缩

#### 3.1.1 原理介绍

节点压缩是一种优化Trie树空间占用率的技术。在传统的Trie树中，每个节点都存储着一个字符和一个指向子节点的指针。对于大量重复的字符，这种存储方式会造成空间浪费。节点压缩通过将重复的字符合并到一个节点中来解决这个问题。

具体而言，节点压缩将具有相同字符的子节点合并为一个节点，并使用一个计数器来记录重复的次数。例如，对于一个包含单词"apple"的Trie树，传统的存储方式会创建5个节点，分别存储字符'a'、'p'、'p'、'l'和'e'。而使用节点压缩后，只需创建3个节点，其中一个节点存储字符'a'和计数器2，另一个节点存储字符'p'和计数器2，最后一个节点存储字符'l'和'e'。

#### 3.1.2 实现方法

节点压缩可以通过修改Trie树的插入和查找算法来实现。在插入时，如果要插入的字符已经存在于当前节点的子节点中，则将该子节点的计数器加1；否则，创建一个新的子节点并将其添加到当前节点。在查找时，如果要查找的字符存在于当前节点的子节点中，则直接返回该子节点；否则，返回空。

### 3.2 分支剪枝

#### 3.2.1 原理介绍

分支剪枝是一种优化Trie树搜索效率的技术。在传统的Trie树中，搜索一个单词需要从根节点开始逐个字符匹配。对于不匹配的单词，这种搜索方式会遍历大量不必要的节点。分支剪枝通过提前判断是否需要继续搜索来解决这个问题。

具体而言，分支剪枝在每个节点上维护一个计数器，记录该节点下所有子节