从零开始学排序：C语言冒泡排序算法教程

# 1. 冒泡排序算法概述

冒泡排序算法是计算机科学领域中最基本的算法之一，以其简单直观而广为人知。该算法重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

冒泡排序虽然易于理解和实现，但在效率上并非最优。特别是对于含有大量元素的列表，冒泡排序的性能可能不尽人意。尽管如此，作为排序算法的入门示例，它有助于理解更复杂的排序技术，比如快速排序、归并排序等。

在接下来的章节中，我们将探讨冒泡排序的理论基础、效率分析、稳定性以及如何在实际编程语言中实现和优化。通过对冒泡排序的深入理解，我们可以更好地掌握排序算法的原理，并将其应用于解决实际问题。

# 2. 冒泡排序的理论基础

## 2.1 算法概念解析

### 2.1.1 排序算法简介

排序算法是计算机科学中一类重要的算法，它的核心目标是将一系列数据按照一定的顺序重新排列。在数据处理、数据库查询、优化算法、搜索技术等领域，排序算法扮演着至关重要的角色。排序算法按其操作方式大致可分为比较排序和非比较排序两大类。比较排序的基本操作是通过比较两个元素的大小来决定其顺序，而非比较排序则采用其他信息来决定排序，例如计数排序、基数排序等。

排序算法的性能评价标准主要包括时间复杂度和空间复杂度。时间复杂度是衡量算法执行效率的重要指标，它描述了算法执行时间与输入数据规模之间的关系；空间复杂度则关注算法在运行过程中所占用的存储空间大小。

### 2.1.2 冒泡排序的工作原理

冒泡排序是一种简单的比较排序算法，它通过重复遍历待排序的数组，比较相邻元素的值，并在必要时交换它们的位置。这一过程持续进行，直至整个数组被遍历完成，最终达到排序的目的。

冒泡排序的名字来源于其工作方式：较小的元素逐渐“冒泡”至数组的前端。在每一趟遍历中，最大的元素会被放置到它的最终位置，因此下一次遍历将排除掉上一次找到的最大元素。

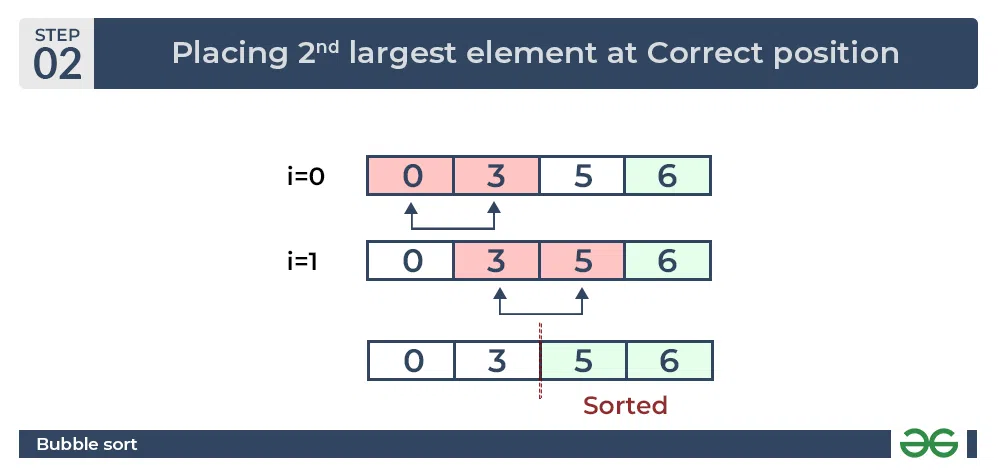
为了更好地理解冒泡排序的工作原理，以下是一个冒泡排序的基本步骤描述：

1. 比较相邻的元素。如果第一个比第二个大，就交换它们两个。
2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后已经排序好的元素。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

## 2.2 算法效率分析

### 2.2.1 时间复杂度分析

冒泡排序的时间复杂度分析，可以帮助我们理解该算法在处理不同大小的数据集时效率如何变化。在最坏的情况下，即数据完全逆序时，冒泡排序需要执行 (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2 次比较操作，因此最坏情况的时间复杂度为 O(n²)。在最好情况下，即数组已经是排序好的，每次只需比较一次，此时只需要 n-1 次比较，时间复杂度为 O(n)。在平均情况下，时间复杂度同样为 O(n²)，因为每一趟排序都有可能交换元素，所以平均起来每次比较都有可能进行一次元素交换。

### 2.2.2 空间复杂度分析

冒泡排序是原地排序算法，这意味着它不需要额外的存储空间（除了输入的数组之外），因此空间复杂度为 O(1)。这种空间效率是冒泡排序在某些特定场景下仍然被使用的原因之一。

## 2.3 算法稳定性探讨

### 2.3.1 稳定排序的定义

排序算法的稳定性是衡量排序算法对相等元素排序后相对位置是否发生变化的标准。如果一个排序算法能保证相等元素之间的相对位置不变，那么这个算法就是稳定的。例如，在一个排序好的数组中，有多个值相同的元素，稳定排序后这些元素的相对位置应与排序前相同。

### 2.3.2 冒泡排序的稳定性讨论

冒泡排序是一种稳定的排序算法。在冒泡排序的过程中，只有当一个元素比它相邻的元素大时，这两个元素才会交换位置。如果遇到两个相等的元素，它们将保持相邻，不会发生交换。因此，冒泡排序不会改变相等元素之间的相对位置，满足稳定性定义。

graph TD
A[开始冒泡排序] --> B[初始化比较次数]
B --> C{遍历数组}
C -->|相等元素| D[保持位置不变]
C -->|不等且前者大| E[交换元素位置]
C -->|完成一趟| F[减少比较次数]
F -->|未完成所有元素| C
F -->|完成所有元素| G[冒泡排序结束]

以上流程图展示冒泡排序中元素的比较和交换过程，通过这一过程可以清晰地看出冒泡排序的稳定性特征。在下一章中，我们将使用C语言来实现冒泡排序，并进一步展开讨论。

# 3. ```
# 第三章：C语言实现冒泡排序

## 3.1 C语言基础知识回顾

### 3.1.1 数据类型与变量

在C语言中，数据类型定义了变量的存储大小和布局、可以使用该类型存储的值的范围，以及可应用于该类型的运算符集合。了解C语言中的基本数据类型是编写任何有效程序的前提。基本的数据类型有以下几种：

- `int`：整数类型，用于存储整数。
- `float`和`double`：浮点类型，用于存储小数。
- `char`：字符类型，用于存储单个字符。
- `void`：无类型，用于指示函数不返回值或不接受参数。

变量是数据的标识符，它提供了数据存储位置的名称。在C语言中，变量必须先声明再使用，声明时需要指定数据类型和变量名，例如：

int number;
float decimal;
char character;

### 3.1.2 控制结构与循环

控制结构允许程序员控制程序的执行流程。最常用的控制结构包括：

- `if`语句：根据条件表达式的结果，决定是否执行一组语句。
- `switch`语句：根据变量的值，执行不同的分支。
- 循环语句：使程序重复执行某段代码，直到满足退出条件。

循环语句有三种主要形式：

- `for`循环：适合已知循环次数的情况。
- `while`循环：当条件为真时，持续执行循环体。
- `do-while`循环：至少执行一次循环体，之后每次条件为真时重复执行。

例如，一个简单的`for`循环用于打印数字1到10：

#include <stdio.h>

int main() {
    for (int i = 1; i <= 10; i++) {
        printf("%d\n", i);
    }
    return 0;
}

## 3.2 冒泡排序的C语言实现

### 3.2.1 算法核心代码解析

冒泡排序的核心思想是通过重复地遍历待排序的数组，比较相邻元素的大小，并在必要时交换它们的位置。每一次遍历，最大的元素会被“冒泡”到数组的末尾。下面是冒泡排序的C语言实现：

#include <stdio.h>

void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n-1; i++) {
        for (int j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                // 交换两个元素的位置
                int temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
}

int main() {
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr)/sizeof(arr[0]);
    bubbleSort(arr, n);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");
    return 0;
}

这段代码首先定义了`bubbleSort`函数，它接受一个整数数组和数组的长度作为参数。外层`for`循环控制遍历的次数，内层`for`循环负责进行实际的比较和交换。若当前元素比后一个元素大，则交换这两个元素的位置。`main`函数中创建并初始化了一个整数数组，调用`bubbleSort`函数对其进行排序，并打印排序后的结果。

### 3.2.2 排序过程可视化

为了更深入地理解冒泡排序的过程，我们可以使用一个简单的数组来跟踪每一步的交换操作：

初始数组: [64, 34, 25, 12, 22, 11, 90]

第 1 轮排序后: [34, 25, 12, 22, 11, 64, 90]
第 2 轮排序后: [25, 12, 22, 11, 34, 64, 90]
第 3 轮排序后: [12, 22, 11, 25, 34, 64, 90]
第 4 轮排序后: [11, 12, 22, 25, 34, 64, 90]
第 5 轮排序后: [11, 12, 22, 25, 34, 64, 90]  // 无变化，排序完成

通过这个过程，我们可以看到，每次外层循环结束后，数组末尾会有一个元素被正确排序。这个简单的可视化有助于理解冒泡排序的机制。

## 3.3 代码优化与异常处理

### 3.3.1 性能优化技巧

冒泡排序的性能可以通过一些简单的方法得到优化。例如，我们可以在每轮遍历后检查数组是否已经排序完成。如果在一轮遍历中没有发生任何交换，则可以提前结束排序。这种优化称为“优化冒泡排序”：

void optimizedBubbleSort(int arr[], int n) {
    int i, j, swapped;
    for (i = 0; i < n-1; i++) {
        swapped = 0;
        for (j = 0; j < n-i-1; j++) {
            if (arr[j] > a