【算法应用指南】：在JavaScript数据删除中运用数据结构与算法

# 1. 数据删除操作概述与算法基础

在现代IT行业中，数据的存储和处理是核心任务之一。数据删除，作为数据维护的基本操作，对于提高系统性能和保护隐私至关重要。本章节将介绍数据删除操作的基本概念，以及支持这些操作的算法基础。

## 1.1 数据删除的重要性

数据删除是数据管理的关键环节，它不仅能够释放存储空间，还能提高数据访问效率。此外，在遵守数据隐私法规方面，精确的数据删除也至关重要。了解数据删除的影响因素，对于设计高效可靠的系统至关重要。

## 1.2 算法基础

为了高效地执行数据删除操作，算法的选择尤为关键。基本的算法包括线性删除、二分查找删除等。更复杂的场景可能需要排序、搜索、分治、动态规划和贪心算法等高级策略。本章将对这些算法进行深入探讨，并分析它们在数据删除中的应用。

通过理解数据删除的基本概念和算法基础，我们可以为后续章节中数据结构的应用、经典算法实践、以及性能评估打下坚实的基础。在下一章中，我们将具体了解数据结构在数据删除中的应用，并分析不同数据结构对删除操作效率的影响。

# 2. 数据结构在数据删除中的应用

## 2.1 常用数据结构简介

### 2.1.1 数组和列表

数组和列表是计算机程序中最基本的数据结构之一。它们被广泛用于存储元素的集合，并提供对集合中元素的访问。在数据删除的上下文中，数组和列表提供基本的增删改查操作，但它们的实现和性能表现存在差异。

数组通常由连续的内存空间构成，这意味着元素可以按序号快速访问。但在数组中进行删除操作时，为了保持连续性，可能需要将后面的元素向前移动，这在大数据量时效率较低。以JavaScript为例，数组的`splice`方法可以用于删除元素，但会导致数组中元素的重新排列。

let arr = [1, 2, 3, 4, 5];
arr.splice(2, 1); // 删除第三个元素
console.log(arr); // 输出: [1, 2, 4, 5]

列表（或链表）则通过指针或引用连接不连续的内存块，因此添加或删除节点时通常只需要改变相邻节点的指针，而不必像数组那样移动元素。列表在删除操作中通常表现更好，尤其适用于频繁的插入和删除操作。

class ListNode {
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

let node1 = new ListNode(1);
let node2 = new ListNode(2);
let node3 = new ListNode(3);
let node4 = new ListNode(4);
let node5 = new ListNode(5);

node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;

// 删除节点3
node2.next = node4; // 跳过node3
console.log(node1); // 输出: [1 -> 2 -> 4 -> 5]

### 2.1.2 栈和队列

栈（Stack）和队列（Queue）是两个更为特殊的线性结构，它们的操作规则各有特点，对数据删除操作有特定的影响。

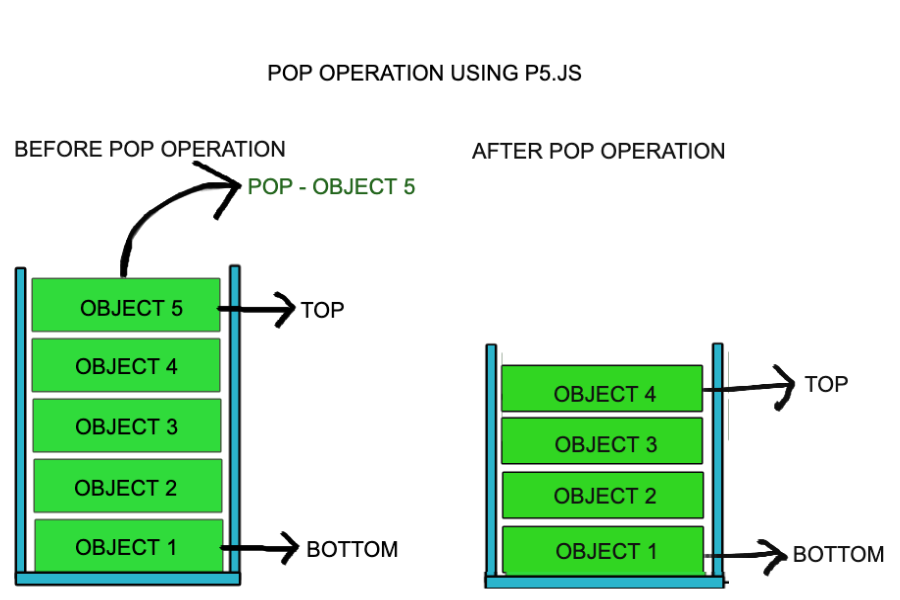
栈是一种后进先出（LIFO）的数据结构，元素添加（push）和删除（pop）都发生在同一端。在栈中，最后一个添加的元素总是第一个被删除，这种特性使得栈在处理某些特定问题（如递归函数的执行）时非常方便。

队列是一种先进先出（FIFO）的数据结构，元素的添加发生在一端（尾部），而删除则发生在另一端（头部）。队列常用于处理任务调度、缓冲区等场景。

这两种数据结构在删除操作上都具有固定的规则，使得它们在某些特定的算法和应用场景中特别有用。

### 2.1.3 链表

链表是一种由节点组成的线性集合，每个节点包含数据部分和至少一个指向前一个或后一个节点的指针。在数据删除时，链表的优势在于可以快速地删除或插入节点，只需调整指针即可。

链表分为单向链表、双向链表和循环链表等类型。单向链表只允许节点在单一方向上链接，而双向链表的节点之间可以双向链接，循环链表的尾部节点连接回头部，形成一个环形结构。

### 2.1.4 树和图

树是一种层级化的数据结构，它由节点组成，节点之间有父子关系。每个节点可以有多个子节点，但只有一个父节点（根节点除外）。树的删除操作涉及到节点的移除，并可能需要更新其子节点的父指针。

图是由顶点（节点）和边组成的复杂数据结构，用于表示元素之间的关系。在图中进行删除操作时，可能需要考虑更多因素，如图的类型（有向或无向）、图的连通性，以及删除后的路径问题等。

## 2.2 数据删除操作中的数据结构选择

### 2.2.1 不同数据结构的删除操作特点

根据数据的类型和操作需求选择合适的数据结构是关键。不同的数据结构对删除操作的支持程度也不同：

- 数组在数据量小且删除操作不频繁时可以是一个好选择，但在处理大量数据且需要频繁修改时可能会导致性能问题。
- 列表（链表）在频繁的插入和删除操作中更加高效，尤其是在数据量未知或需要动态扩展时。
- 栈和队列因其独特的数据存取规则，在特定应用场景中可以提供简单的解决方案。
- 树和图结构适用于复杂的数据关系和层次化数据，删除操作需要关注数据结构的连通性和完整性。

### 2.2.2 数据结构与删除效率分析

删除操作的效率分析需要考虑以下几个方面：

- 时间复杂度：不同数据结构在删除操作中的时间消耗不同。例如，数组中的删除操作可能导致O(n)的复杂度，而链表则能保持在O(1)。
- 空间复杂度：数据结构需要的空间以及删除操作对空间的消耗也应考虑在内。
- 算法复杂度：在处理更复杂的数据结构（如树和图）时，相关算法（如深度优先搜索和广度优先搜索）的时间复杂度也应纳入考量。

## 2.3 数据结构的优化策略

### 2.3.1 空间复杂度的考量

优化数据结构的空间复杂度可以从以下几个方面入手：

- 压缩存储：例如，使用稀疏矩阵来存储只有少数非零元素的大型矩阵。
- 空间复用：在数据删除操作中，复用被删除元素的存储空间可以降低整体的空间开销。

### 2.3.2 时间复杂度的优化

时间复杂度的优化依赖于合理的选择和应用数据结构：

- 数据预处理：在删除前对数据进行排序或建立索引可以降低查找元素的时间成本。
- 惰性删除：在某些情况下，可以采用标记删除而非立即删除，这样可以减少删除操作的频率和执行时间。
- 分区存储：对于不同的数据访问模式，使用不同的数据结构进行存储可以减少不必要的数据遍历。

通过上述策略，可以使得在面对数据删除操作时，更加高效和有针对性地应用数据结构，从而优化整体性能和资源消耗。

# 3. 经典算法在数据删除中的实践

在数据管理中，高效的数据删除操作对于系统性能和存储资源的优化至关重要。本章节将深入探讨几种经典算法在数据删除操作中的具体应用，以及如何通过这些算法提高删除效率和数据处理的速度。

## 3.1 排序算法在删除操作中的应用

### 3.1.1 常见排序算法回顾

排序算法是编程中的基础，也是处理数据删除操作前的重要步骤。有效的排序算法可以确保数据在删除之前是有序的，从而提高整体处理的效率。常见的排序算法包括冒泡排序、选择排序、插入排序、归并排序、快速排序和堆排序等。

冒泡排序通过重复遍历要排序的数列，比较相邻两个元素，如果顺序错误就交换它们的位置，直到没有需要交换的为止。选择排序则是通过选择未排序部分的最小（大）值，将其放置到排序序列的起始位置，重复此操作直到整个序列排序完毕。插入排序则是在已排序序列中，找到相应的插入位置并插入新的数据元素。

归并排序采用了分治法的思想，将数列分成两半，分别排序，然后合并。快速排序采用分治策略，通过一个基准值将数列分为独立的两部分，一边的数都比基准值小，另一边的数都比基准值大，然后递归排序子序列。堆排序则利用堆这种数据结构所设计的一种排序算法，通过建立大顶堆或小顶堆的方式，将最大（小）元素放到堆顶，并完成排序。

### 3.1.2 排序算法在数据删除前的预处理

在数据删除前进行预处理通常涉及到快速定位到需要删除的元素，这需要数据在某种程度上是有序的。例如，在一个已排序的数组中，可以通过二分搜索快速定位到目标元素的位置，然后进行删除操作。

例如，假设我们需要删除一个有序数组中的某个元素`value`：

def delete_element(sorted_array, value):
    left, right = 0, len(sorted_array) - 1
    while left <= right:
        mid = (left + right) // 2
        if sorted_array[mid] == value:
            # 找到元素，执行删除操作
            # 具体删除操作取决于数组是如何存储的
            return sorted_array[:mid] + sorted_array[mid+1:]
        elif sorted_array[mid] < value:
            left = mid + 1