MATLAB拟合函数实战技巧:解决常见拟合问题,掌握数据拟合的艺术
发布时间: 2024-06-06 00:16:47 阅读量: 158 订阅数: 42 


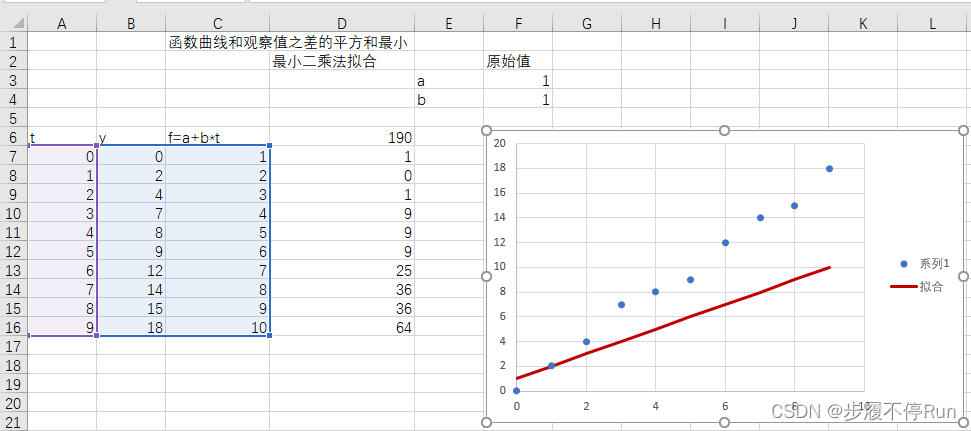
使用matlab进行数据拟合
# 1. MATLAB拟合函数概述**
MATLAB拟合函数是用于找到一组数据点的最佳数学模型的强大工具。这些函数允许用户通过最小化误差函数来拟合各种类型的函数到数据。拟合函数在许多领域都有应用,包括数据分析、建模和预测。
拟合函数的工作原理是通过迭代地调整模型参数,直到找到与数据最匹配的模型。MATLAB提供了多种拟合函数,每种函数都适用于特定类型的数据和模型。常见的拟合函数包括线性回归、非线性回归和多项式拟合。
# 2. MATLAB拟合函数的理论基础
### 2.1 拟合函数的数学原理
#### 2.1.1 线性回归
线性回归是一种拟合函数,用于拟合一组数据点到一条直线。其数学表达式为:
```
y = mx + b
```
其中:
- `y` 是因变量
- `x` 是自变量
- `m` 是斜率
- `b` 是截距
线性回归的目标是找到一组参数 `m` 和 `b`,使得拟合直线与数据点之间的误差最小。误差通常使用均方误差 (MSE) 来衡量,其计算公式为:
```
MSE = (1/n) * Σ(y_i - (mx_i + b))^2
```
其中:
- `n` 是数据点的数量
- `y_i` 是第 `i` 个数据点的因变量值
- `x_i` 是第 `i` 个数据点的自变量值
#### 2.1.2 非线性回归
非线性回归是一种拟合函数,用于拟合一组数据点到一条非线性曲线。其数学表达式可以非常复杂,具体形式取决于拟合曲线的类型。
常见非线性回归模型包括:
- 多项式回归:`y = a + bx + cx^2 + ...`
- 指数回归:`y = ae^(bx)`
- 对数回归:`y = a + b * log(x)`
非线性回归的目标也是找到一组参数,使得拟合曲线与数据点之间的误差最小。误差的衡量方法与线性回归类似,通常使用均方误差或其他误差度量。
### 2.2 拟合函数的评估指标
拟合函数的评估指标用于衡量拟合函数的性能。常用的评估指标包括:
#### 2.2.1 均方误差 (MSE)
均方误差 (MSE) 是衡量拟合函数与数据点之间误差的常用指标。其计算公式如上文所述。MSE 越小,表示拟合函数与数据点之间的误差越小,拟合效果越好。
#### 2.2.2 决定系数 (R^2)
决定系数 (R^2) 是另一个衡量拟合函数性能的指标。其计算公式为:
```
R^2 = 1 - (MSE / Var(y))
```
其中:
- `Var(y)` 是因变量值的方差
决定系数表示拟合函数解释因变量变异的比例。R^2 越接近 1,表示拟合函数解释的变异越多,拟合效果越好。
# 3. MATLAB拟合函数的实践技巧
### 3.1 数据预处理
#### 3.1.1 数据清洗和转换
在拟合函数之前,对数据进行预处理至关重要。数据预处理包括数据清洗和转换,以确保数据质量并提高拟合精度。
**数据清洗**
数据清洗涉及识别和删除异常值、缺失值和噪声。异常值是明显偏离数据集其余部分的数据点,可能由测量误差或其他因素引起。缺失值是缺少数据的点,需要用适当的方法填充或删除。噪声是随机波动,会干扰拟合过程。
**数据转换**
数据转换包括将数据从一种格式转换为另一种格式,以提高拟合精度。常见的转换包括:
- **标准化:**将数据转换为具有均值为 0 和标准差为 1 的分布。
- **归一化:**将数据转换为 0 到 1 之间的范围。
- **对数转换:**对数据取对数,以处理偏态或非正态分布。
### 3.1.2 特征工程
特征工程是创建或修改特征的过程,以提高拟合模型的性能。特征是用于拟合函数的数据属性。特征工程技术包括:
- **特征选择:**选择与目标变量最相关的特征。
- **特征提取:**创建新的特征,通过组合或转换现有特征。
- **特征缩放:**将特征缩放为相同范围,以防止某些特征对拟合过程产生过大影响。
### 3.2 拟合函数的选择和参数优化
#### 3.2.1 常见拟合函数的优缺点
MATLAB 提供了各种拟合函数,每种函数都有其优点和缺点。常见的拟合函数包括:
| 拟合函数 | 优点 | 缺点 |
|---|---|---|
| 线性回归 | 简单、易于解释 | 对非线性数据拟合效果较差 |
| 多项式回归 | 适用于复杂非线性数据 | 容易过拟合 |
| 指数回归 | 用于拟合指数增长或衰减数据 | 对噪声敏感 |
| 对数回归 | 用于拟合逻辑或二分类数据 | 要求数据可线性分离 |
#### 3.2.2 参数优化算法
拟合函数通常具有多个参数,需要优化以获得最佳拟合。MATLAB 提供了各种参数优化算法,包括:
- **最小二乘法:**最小化拟合函数与数据点之间的平方误差。
- **梯度下降:**沿着梯度负方向迭代更新参数,以最小化目标函数。
- **牛顿法:**使用牛顿法迭代更新参数,以二次收敛速度找到极小值。
**代码块:**
```matlab
% 使用最小二乘法拟合线性回归模型
model = fitlm(x, y);
% 使用梯度下降优化多项式回归模型的参数
options = optimset('Algorithm', 'gradientdescent');
model = fitlm(x, y, 'poly2', 'Options', options);
% 使用牛顿法优化指数回归模型的参数
model = fitnlm(x, y, 'exp1');
```
**逻辑分析:**
* `fitlm` 函数使用最小二乘法拟合线性回归模型。
* `fitlm` 函数使用梯度下降算法优化多项式回归模型的参数。
* `fitnlm` 函数使用牛顿法优化指数回归模型的参数。
# 4. MATLAB拟合函数的进阶应用
### 4.1 复杂数据拟合
#### 4.1.1 多项式拟合
**理论基础:**
多项式拟合是一种拟合函数,它使用多项式方程来拟合数据。多项式方程的形式为:
```
y = a0 + a1*x + a2*x^2 + ... + an*x^n
```
其中,`y` 是因变量,`x` 是自变量,`a0`, `a1`, ..., `an` 是多项式的系数。
**MATLAB实现:**
```matlab
% 数据
x = [1, 2, 3, 4, 5];
y = [2, 4, 8, 16, 32];
% 多项式拟合
p = polyfit(x, y, 2);
% 拟合曲线
x_fit = linspace(min(x), max(x), 100);
y_fit = polyval(p, x_fit);
% 绘制拟合曲线
plot(x, y, 'o', x_fit, y_fit, '-');
legend('数据', '多项式拟合');
```
**逻辑分析:**
* `polyfit` 函数用于进行多项式拟合,其中 `x` 是自变量数据,`y` 是因变量数据,`2` 表示拟合多项式的次数。
* `linspace` 函数用于生成用于绘制拟合曲线的均匀间隔的自变量数据。
* `polyval` 函数用于计算指定自变量值下的多项式值。
* 绘图部分展示了原始数据点和拟合曲线。
#### 4.1.2 分段拟合
**理论基础:**
分段拟合是一种拟合函数,它将数据分成多个子区间,并在每个子区间内使用不同的拟合函数。分段拟合可以提高复杂数据的拟合精度。
**MATLAB实现:**
```matlab
% 数据
x = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
y = [0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100];
% 分段拟合
breakpoints = [0, 5, 10];
p1 = polyfit(x(1:5), y(1:5), 1);
p2 = polyfit(x(6:10), y(6:10), 2);
% 拟合曲线
x_fit = linspace(min(x), max(x), 100);
y_fit = zeros(size(x_fit));
for i = 1:length(breakpoints)
if x_fit(i) <= breakpoints(i)
y_fit(i) = polyval(p1, x_fit(i));
else
y_fit(i) = polyval(p2, x_fit(i));
end
end
% 绘制拟合曲线
plot(x, y, 'o', x_fit, y_fit, '-');
legend('数据', '分段拟合');
```
**逻辑分析:**
* `breakpoints` 变量定义了分段拟合的断点。
* `polyfit` 函数分别用于拟合每个子区间的数据。
* 循环用于根据断点计算每个自变量值下的拟合值。
* 绘图部分展示了原始数据点和分段拟合曲线。
# 5. MATLAB拟合函数的实战案例
### 5.1 实验数据拟合
**5.1.1 实验数据的线性拟合**
**实验数据:**
```
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
y = [2, 4, 6, 8, 10, 12, 14, 16, 18, 20];
```
**线性拟合:**
```
% 拟合线性函数
p = polyfit(x, y, 1);
% 计算拟合直线的方程
y_fit = polyval(p, x);
% 绘制拟合直线和原始数据
plot(x, y, 'o', x, y_fit, '-r');
legend('原始数据', '拟合直线');
```
### 5.1.2 实验数据的非线性拟合
**实验数据:**
```
x = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
y = [0, 0.84, 1.55, 2.14, 2.62, 3.01, 3.33, 3.60, 3.83, 4.00];
```
**非线性拟合(指数函数):**
```
% 拟合指数函数
p = polyfit(x, log(y), 1);
% 计算拟合指数函数
y_fit = exp(polyval(p, x));
% 绘制拟合指数函数和原始数据
plot(x, y, 'o', x, y_fit, '-r');
legend('原始数据', '拟合指数函数');
```
0
0





