MATLAB拟合函数在教育和研究中的应用：从学生项目到科学突破，让数据分析点亮知识之光

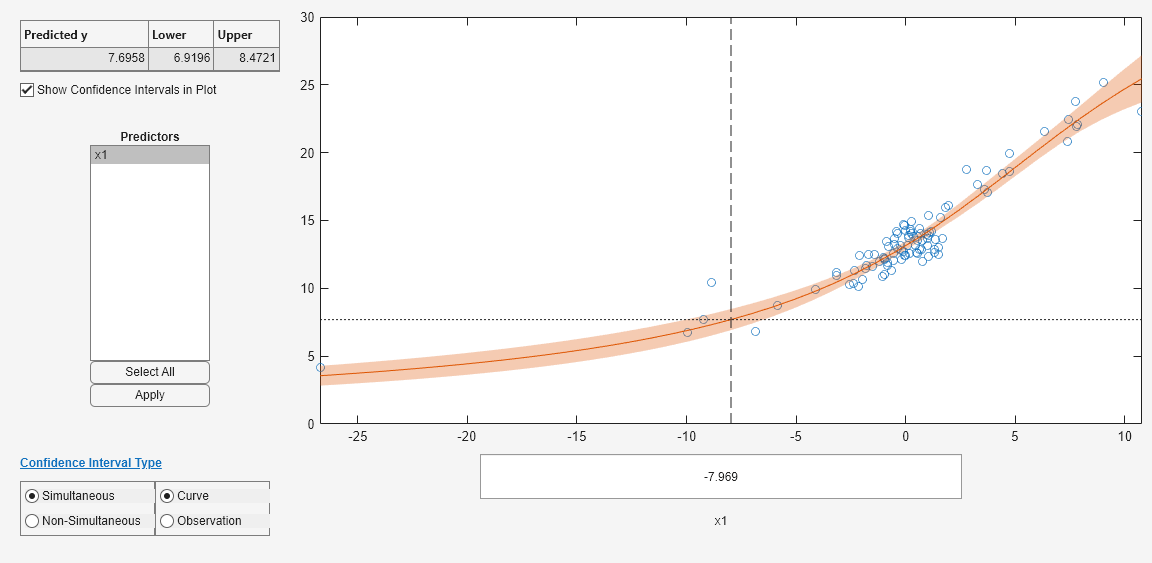
# 1. MATLAB拟合函数概述

MATLAB拟合函数是一组强大的工具，用于从数据中提取有意义的信息。这些函数允许用户创建数学模型来近似给定数据集的趋势和模式。通过拟合函数，研究人员和工程师可以分析数据、进行预测并优化系统。

MATLAB提供各种拟合函数类型，包括线性、多项式、非线性以及自定义函数。这些函数基于最小二乘法和最大似然法等统计方法，可确保拟合模型准确且可靠。拟合函数的评估和验证至关重要，以确保模型的有效性和预测能力。

# 2. MATLAB拟合函数的理论基础

### 2.1 拟合函数的类型和选择

拟合函数是用来描述数据集中点之间的关系的数学方程。在MATLAB中，有各种类型的拟合函数可供选择，包括：

- 线性拟合：描述一条直线，用于拟合具有线性关系的数据。
- 多项式拟合：描述一条曲线，用于拟合具有非线性关系的数据。
- 指数拟合：描述一个指数曲线，用于拟合具有指数关系的数据。
- 对数拟合：描述一个对数曲线，用于拟合具有对数关系的数据。
- 高斯拟合：描述一个高斯分布曲线，用于拟合具有正态分布的数据。

选择合适的拟合函数取决于数据的性质和要拟合的关系类型。

### 2.2 最小二乘法和最大似然法

拟合函数的拟合质量可以通过最小化误差来评估。有两种常用的方法来最小化误差：最小二乘法和最大似然法。

**最小二乘法**通过最小化拟合函数和数据点之间的平方误差来拟合函数。它假设误差是正态分布的，并且是独立的。

**最大似然法**通过最大化拟合函数的参数值使似然函数最大的值来拟合函数。它假设数据是从特定分布中生成的，并且误差服从该分布。

### 2.3 拟合函数的评估和验证

拟合函数的拟合质量可以通过以下指标来评估：

- **残差平方和 (RSS)**：拟合函数和数据点之间的平方误差之和。
- **决定系数 (R^2)**：拟合函数解释数据变异的程度。
- **调整后的决定系数 (Adj. R^2)**：考虑了拟合函数的自由度，提供了更准确的拟合质量度量。
- **均方根误差 (RMSE)**：拟合函数和数据点之间的平均误差的平方根。

拟合函数的验证涉及使用独立的数据集来测试其预测能力。如果拟合函数在验证数据集上表现良好，则表明它具有良好的泛化能力。

**代码示例：**

% 生成数据
x = linspace(-10, 10, 100);
y = sin(x) + 0.1 * randn(size(x));

% 拟合正弦函数
fit_func = fit(x', y', 'sin1');

% 评估拟合质量
r2 = fit_func.rsquare;
rmse = sqrt(mean((y - fit_func(x')).^2));

% 打印结果
disp("决定系数 (R^2): " + r2);
disp("均方根误差 (RMSE): " + rmse);

**代码逻辑分析：**

* `linspace` 函数生成一个等间隔的数据点序列。
* `fit` 函数拟合正弦函数到数据。
* `rsquare` 属性返回拟合函数的决定系数。
* `mean` 函数计算数据点和拟合函数之间的平方误差的平均值。
* `sqrt` 函数计算均方根误差。

# 3. MATLAB拟合函数的实践应用

### 3.1 学生项目中的拟合函数应用

#### 3.1.1 线性拟合和多项式拟合

在学生项目中，拟合函数经常用于对实验数据进行建模和分析。线性拟合和多项式拟合是最常用的拟合类型，它们可以揭示数据中的线性或非线性趋势。

**线性拟合**

% 给定数据点
x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8, 10];