MATLAB拟合函数的性能评估：度量拟合结果的准确性和鲁棒性，让数据分析更可靠

# 1. 拟合函数的基本原理

拟合函数是一种数学模型，用于根据一组给定的数据点，估计一个函数。它通过找到一个函数，使得函数的输出值与给定的数据点之间的误差最小化。

拟合函数的基本原理是使用一个数学函数来近似一组数据点。这个函数可以是线性的、非线性的、多项式的或任何其他形式。拟合函数的目标是找到一个函数，使得函数的输出值与给定的数据点之间的误差最小。

# 2. 拟合函数的评估方法

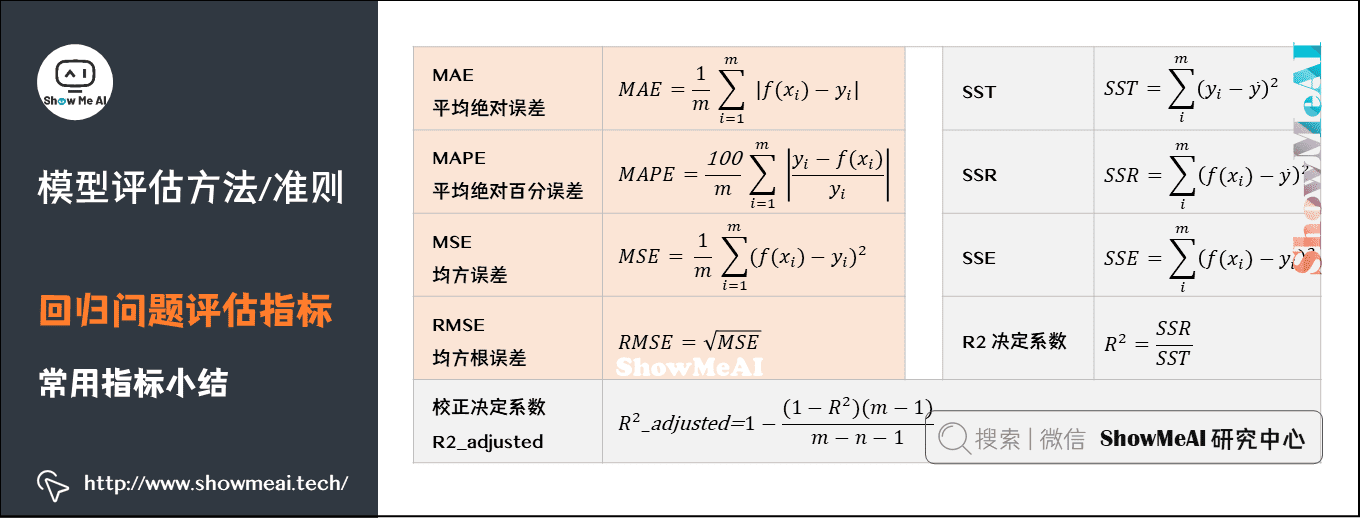
在本章节中，我们将探讨评估拟合函数性能的不同方法。拟合函数的评估对于确定其准确性、鲁棒性和适用性至关重要。

### 2.1 度量拟合结果的准确性

准确性是拟合函数评估的关键方面。它衡量拟合函数在预测目标变量方面与实际值之间的接近程度。以下是一些常用的准确性度量：

#### 2.1.1 均方误差 (MSE)

MSE 是预测值和实际值之间的平方误差的平均值。它衡量拟合函数对预测目标变量的总体准确性。

MSE = (1/n) * Σ(y_i - f(x_i))^2

其中：

* n 是数据点的数量
* y_i 是实际值
* f(x_i) 是预测值

#### 2.1.2 平均绝对误差 (MAE)

MAE 是预测值和实际值之间的绝对误差的平均值。它衡量拟合函数对预测目标变量的平均准确性。

MAE = (1/n) * Σ|y_i - f(x_i)|

#### 2.1.3 决定系数 (R²)

R² 是拟合函数解释目标变量变化的程度的度量。它表示预测值与实际值之间的相关性。

R² = 1 - (Σ(y_i - f(x_i))^2 / Σ(y_i - y_mean)^2)

其中：

* y_mean 是实际值的平均值

### 2.2 评估拟合函数的鲁棒性

鲁棒性是指拟合函数在处理噪声和异常值时的稳定性。以下是一些评估拟合函数鲁棒性的方法：

#### 2.2.1 抗噪声性

抗噪声性衡量拟合函数在存在噪声数据时的性能。噪声数据是指包含随机误差的数据。

#### 2.2.2 抗异常值性

抗异常值性衡量拟合函数在存在异常值时的性能。异常值是与其他数据点明显不同的数据点。

# 3.1 线性拟合

#### 3.1.1 线性回归模型

线性回归模型是一种常见的线性拟合方法，它旨在找到一条直线来近似一组数据点。MATLAB 中的 `polyfit` 函数可用于执行线性回归。

% 数据点
x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8, 10];

% 线性回归
p = polyfit(x, y, 1);

% 绘制拟合直线
plot(x, y, 'o');
hold on;
plot(x, polyval(p, x), 'r-');
legend('数据点', '拟合直线');

**参数说明：**

* `x`: 自变量数据点
* `y`: 因变量数据点
* `1`: 拟合多项式的阶数（1 表示线性回归）

**代码逻辑：**

1. 使用 `polyfit` 函数拟合一条线性回归直线，并存储在 `p` 中。
2. 绘制原始数据点和拟合直线。
3. 使用 `legend` 函数添加图例。

#### 3.1.2 多项式拟合

多项式拟合是一种更通用的线性拟合方法，它允许拟合任意阶数的多项式。MATLAB 中的 `polyfit` 函数也可以用于多项式拟合。

% 数据点
x = [1, 2, 3, 4, 5];
y = [2, 4, 8, 16, 32];

% 多项式拟合
p = polyfit(x, y, 2);

% 绘制拟合多项式
plot(x, y, 'o');
hold on;
plot(x, polyval(p, x), 'r-');
legend('数据点', '拟合多项式');

**参数说明：**

* `x`: 自变量数据点
* `y`: 因变量数据点
* `2`: 拟合多项式的阶数（2 表示二次多项式）

**代码逻辑：**

1. 使用 `polyfit` 函数拟合一个二次多项式，并存储在 `p` 中。
2. 绘制原始数据点和拟合多项式。
3. 使用 `legend` 函数添加图例。

# 4. MATLAB拟合函数的进阶应用

### 4.1 拟合函数的优化

在某些情况下，拟合函数的默认参数可能无法产生最佳拟合结果。为了提高拟合精度，可以对拟合函数进行优化，调整其参数以最小化误差度量。

#### 4.1.1 梯度下降法

梯度下降法是一种迭代优化算法，通过重复移动参数来最小化目标函数（例如，均方误差）。在每一步中，算法计算目标函数相对于参数的梯度，并沿着梯度负方向移动参数，从而减小目标函数的值。

% 使用梯度下降法优化线性拟合函数
data = [1, 2; 3, 4; 5, 6];
initial_params = [0, 0]; % 初始参数

% 定义目标函数（均方误差）
mse = @(params) mean((data(:, 2) - (params(1) * data(:, 1) + params(2))).^2);

% 设置学习率
learning_rate = 0.01;

% 迭代优化
for i = 1:1000
    params = pa