ElasticNet回归在人工智能领域的应用：机器学习和深度学习，赋能智能化未来

# 1. ElasticNet回归的基本原理

ElasticNet回归是一种线性回归模型，结合了L1正则化（Lasso）和L2正则化（Ridge）的优点。它通过在目标函数中添加一个惩罚项来实现变量选择和模型正则化。

**目标函数：**

min (1/2n) ||y - Xβ||^2 + α||β||_1 + (1 - α)||β||_2^2

其中：

* y 是目标变量
* X 是特征矩阵
* β 是回归系数
* n 是样本数量
* α 是正则化参数（0 ≤ α ≤ 1）

**L1正则化：**

L1正则化项（||β||_1）鼓励系数稀疏，即使一些系数为零。这有助于进行变量选择，剔除不重要的特征。

**L2正则化：**

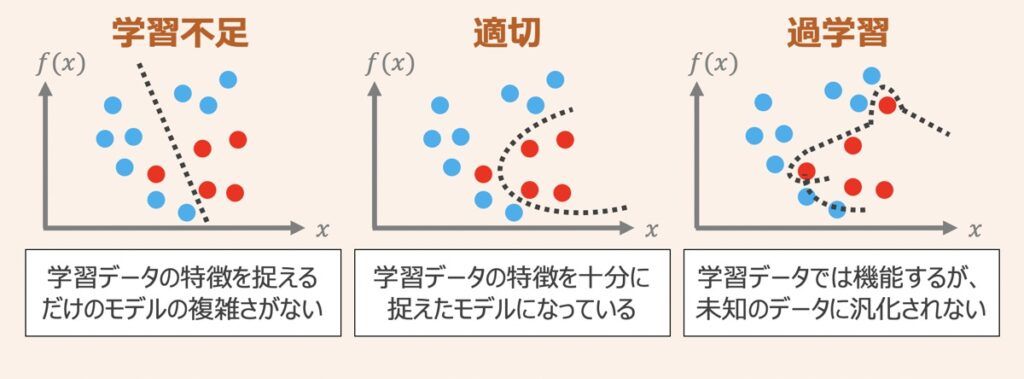
L2正则化项（||β||_2^2）鼓励系数平滑，即防止系数过大。这有助于防止过拟合，提高模型的泛化能力。

# 2. ElasticNet 回归在机器学习中的应用

### 2.1 监督学习中的 ElasticNet 回归

#### 2.1.1 线性回归和逻辑回归中的 ElasticNet

**线性回归**

在线性回归中，ElasticNet 回归通过在损失函数中添加 L1 和 L2 正则化项来解决过拟合问题。损失函数如下：

loss = (1/2n) * ||y - Xw||^2 + α * ||w||_1 + β * ||w||_2^2

其中：

* `n` 是样本数量
* `y` 是目标变量
* `X` 是特征矩阵
* `w` 是模型权重
* `α` 是 L1 正则化参数
* `β` 是 L2 正则化参数

L1 正则化通过惩罚权重向量的绝对值之和来促进稀疏性，而 L2 正则化通过惩罚权重向量的平方和来促进权重向量的平滑。

**逻辑回归**

在逻辑回归中，ElasticNet 回归同样可以应用于解决过拟合问题。损失函数如下：

loss = -(1/n) * Σ[y * log(p) + (1 - y) * log(1 - p)] + α * ||w||_1 + β * ||w||_2^2

其中：

* `n` 是样本数量
* `y` 是目标变量（二分类）
* `p` 是模型预测的概率
* `w` 是模型权重
* `α` 是 L1 正则化参数
* `β` 是 L2 正则化参数

#### 2.1.2 决策树和支持向量机中的 ElasticNet

**决策树**

在决策树中，ElasticNet 回归可以通过在节点分裂准则中添加正则化项来防止过拟合。正则化项如下：

regularization_term = α * ||w||_1 + β * ||w||_2^2

其中：

* `α` 是 L1 正则化参数
* `β` 是 L2 正则化参数

**支持向量机**

在支持向量机中，ElasticNet 回归可以通过在目标函数中添加正则化项来解决过拟合问题。目标函数如下：

objective = (1/2) * ||w||^2 + C * Σ[max(0, 1 - y * (w^T * x + b))] + α * ||w||_1 + β * ||w||_2^2

其中：

* `w` 是模型权重
* `C` 是正则化参数
* `y` 是目标变量
* `x` 是特征向量
* `b` 是偏置项
* `α` 是 L1 正则化参数
* `β` 是 L2 正则化参数

### 2.2 无监督学习中的 ElasticNet 回归

#### 2.2.1 聚类中的 ElasticNet

在聚类中，ElasticNet 回归可以通过在目标函数中添加正则化项来促进稀疏聚类。目标函数如下：

objective = Σ[||x - c||^2] + α * ||c||_1 + β * ||c||_2^2

其中：

* `x` 是数据点
* `c` 是聚类中心
* `α` 是 L1 正则化参数
* `β` 是 L2 正则化参数

#### 2.2.2 降维中的 ElasticNet

在降维中，ElasticNet 回归可以通过在目标函数中添加正则化项来促进稀疏降维。目标函数如下：

objective = (1/2) * ||X - WZ||^2 + α * ||W||_1 + β * ||W||_2^2

其中：

* `X` 是原始数据矩阵
* `W` 是降维矩阵
* `Z` 是降维后的数据矩阵
* `α` 是 L1 正则化参数
* `β` 是 L2 正则化参数

# 3.1 卷积神经网络中的 ElasticNet 回归

#### 3.1.1 图像分类中的 ElasticNet

在图像分类任务中，卷积神经网络 (CNN) 已成为一种强大的工具。ElasticNet 回归可以增强 CNN 的性能，方法是引入正则化项来惩罚模型的复杂性。

import tensorflow as tf

# 创建 CNN 模型
model = tf.keras.models.Sequential([
    tf.keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
    tf.keras.layers.MaxPo