ElasticNet回归的理论根基：凸优化和正则化理论，深入理解算法原理

# 1. ElasticNet回归概述

ElasticNet回归是一种机器学习算法，用于解决回归问题。它结合了L1正则化和L2正则化，以提高模型的泛化能力和鲁棒性。ElasticNet回归模型的优点包括：

- **稀疏性：**L1正则化可以使模型中的某些特征系数为零，从而产生稀疏模型，有助于特征选择。
- **稳定性：**L2正则化可以防止模型过拟合，提高模型的稳定性。
- **可解释性：**稀疏模型更容易解释，因为只有少数几个特征对模型的预测有显著影响。

# 2. ElasticNet回归的理论基础

### 2.1 凸优化理论

#### 2.1.1 凸函数和凸集

**凸函数：**

* 定义：对于定义域为凸集的函数 f(x)，如果对于任意 x1, x2 ∈ dom(f) 和 0 ≤ λ ≤ 1，有 f(λx1 + (1 - λ)x2) ≤ λf(x1) + (1 - λ)f(x2)，则称 f(x) 为凸函数。
* 几何意义：凸函数的图像是一个凸集，即任意两点连线上的点都位于图像上方。

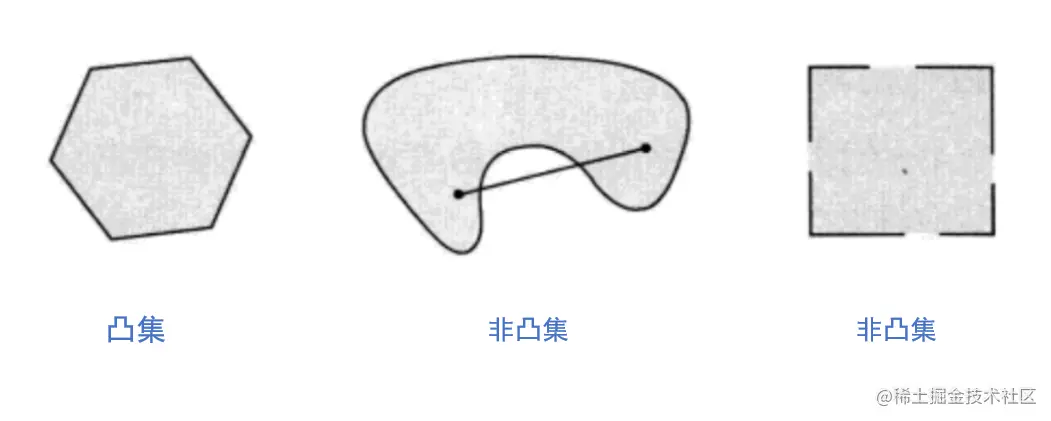
**凸集：**

* 定义：对于集合 S，如果对于任意 x1, x2 ∈ S 和 0 ≤ λ ≤ 1，有 λx1 + (1 - λ)x2 ∈ S，则称 S 为凸集。
* 几何意义：凸集是一个形状规则的集合，任意两点连线上的点都属于该集合。

#### 2.1.2 凸优化问题的求解

凸优化问题是指目标函数和约束条件都是凸函数的优化问题。凸优化问题的求解具有以下特点：

* **局部最优即全局最优：**对于凸优化问题，任何局部最优解都是全局最优解。
* **高效的求解算法：**存在高效的算法（如内点法、次梯度法）可以求解凸优化问题。

### 2.2 正则化理论

#### 2.2.1 正则化方法概述

正则化是一种在机器学习中常用的技术，其目的是通过在目标函数中加入惩罚项来防止过拟合。正则化方法有多种，包括：

* L1正则化（Lasso）
* L2正则化（Ridge）
* ElasticNet正则化（结合L1和L2正则化）

#### 2.2.2 L1正则化和L2正则化

**L1正则化（Lasso）：**

* 目标函数：min(f(x) +