红黑树原理与实现：数据结构高级技巧全解

# 1. 红黑树的基础概念和特性

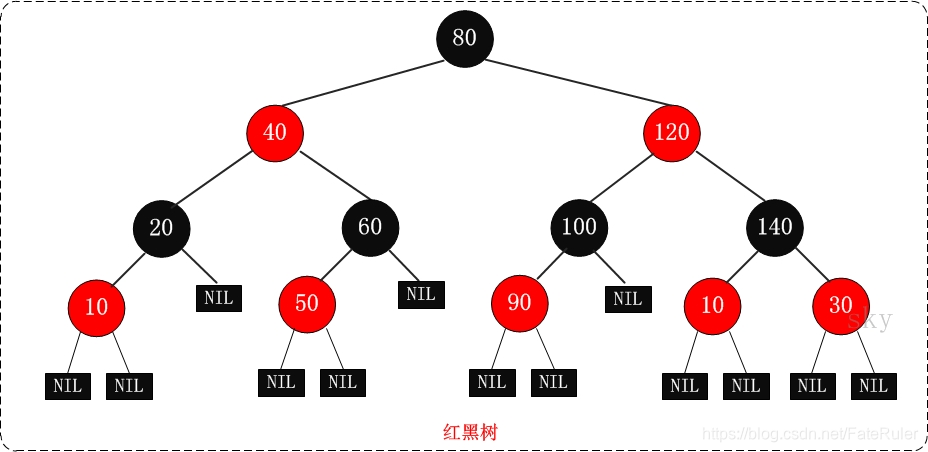
红黑树是一种自平衡的二叉搜索树，在数据库、文件系统等许多领域有着广泛的应用。它的特别之处在于能够在每个节点上增加一个存储位来表示节点的颜色，可以是红色或黑色。通过这种方式，红黑树确保没有任何一条路径会比其他路径长出两倍，因而是近似平衡的。

## 1.1 红黑树的颜色定义

在红黑树中，每个节点都遵循以下的颜色规则：
- 节点要么是红色，要么是黑色。
- 根节点总是黑色的。
- 所有叶子节点（NIL节点，空节点）都是黑色的。
- 如果一个节点是红色的，则它的两个子节点都是黑色的（不能有两个连续的红色节点）。
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些规则共同保障了树的平衡性，从而保证了操作的效率。

## 1.2 红黑树的特性

红黑树的这些特性确保了其操作的高效性，主要体现在以下几个方面：
- **近似平衡**：尽管红黑树不是完全平衡的，但通过维持上述颜色性质，任何一条从根节点到叶子节点的路径不会超过其他路径的两倍长度。
- **高效搜索**：红黑树是二叉搜索树的改进版本，因此它继承了二叉搜索树在搜索方面的优势。
- **插入和删除的性能**：红黑树能够高效地插入和删除节点，并在每次操作后快速地自我平衡，这使得其性能保持在一个较高的水平。

理解了红黑树的基础概念和特性后，我们将在下一章深入探讨其详细的理论基础。

# 2. 红黑树的详细理论基础

## 2.1 红黑树的颜色性质

### 2.1.1 颜色的定义和规则

在红黑树中，每个节点都会被涂成红色或黑色。这是红黑树的核心特性之一，并且红黑树的平衡性是通过节点颜色的严格规则来维护的。具体颜色规则如下：

- 根节点必须是黑色。
- 每个红色节点的两个子节点必须都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）。
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

这些规则保证了树的平衡性，使得红黑树在插入和删除操作中保持了对数级别的高度，从而保证了查找、插入和删除操作的效率。

### 2.1.2 颜色变化的基本逻辑

颜色变化是红黑树中调整树平衡的关键操作。当发生插入或删除操作后，如果破坏了红黑树的基本规则，需要通过一系列的颜色变更和节点旋转来修复。颜色变化通常涉及以下几种情况：

- 当插入一个红色节点时，如果其父节点也是红色，那么需要将祖父节点的一个子节点变红，同时将祖父节点变黑。如果这个操作继续破坏了规则，还需要递归地向上进行调整。
- 在删除操作中，如果删除一个黑色节点导致不满足规则，可能需要通过重新着色、旋转操作或引入一个“额外黑色”来解决问题。

颜色变化通常伴随着节点的旋转，这种复合操作能确保在保证红黑树基本规则的同时，树结构仍然保持平衡。

## 2.2 红黑树的节点操作

### 2.2.1 插入操作的原理

红黑树的插入操作原理首先和二叉搜索树的插入相同，即将新节点作为叶子节点添加到树中，然后通过一系列的颜色变更和旋转操作，恢复树的红黑属性。插入操作可能涉及以下步骤：

1. 将新节点着为红色。
2. 执行正常的二叉搜索树插入。
3. 如果新节点的父节点是黑色，插入完成。
4. 如果父节点是红色，需要进行额外操作来维护红黑树的性质。

### 2.2.2 删除操作的原理

红黑树的删除操作原理同样基于二叉搜索树的删除机制，但在删除后需要执行特殊的调整来保证红黑树的性质不受破坏。删除操作可能涉及以下步骤：

1. 如果要删除的节点有两个子节点，用其后继节点（或前驱节点）替换。
2. 删除节点，如果被删除的是红色节点，不会影响树的性质；如果是黑色节点，可能需要进行调整。
3. 使用旋转和重新着色的方法来维护红黑树的性质。

### 2.2.3 节点旋转的规则和目的

节点旋转是保持红黑树平衡的关键操作，分为左旋和右旋。旋转规则及目的是为了解决颜色违规问题，确保树在插入和删除操作后仍然平衡。

- **左旋**：对节点y进行左旋，假设其右孩子为x。左旋后，x的左孩子成为y的右孩子，y成为x的左孩子。
- **右旋**：对节点x进行右旋，假设其左孩子为y。右旋后，y的右孩子成为x的左孩子，x成为y的右孩子。

旋转操作不仅可以帮助调整节点颜色以保持平衡，还能确保树维持二叉搜索树的特性。这使得红黑树在面对动态数据集时，仍然可以高效地执行查找、插入和删除操作。

在下一章节中，我们将深入探讨红黑树的实践操作技巧，包括如何实现插入和删除功能，以及如何处理各种颜色和结构上的调整。

# 3. 红黑树的实践操作技巧

## 3.1 红黑树的插入实现

### 3.1.1 实现插入功能的步骤

在红黑树中插入一个节点是一个复杂的过程，涉及到多个步骤来确保树的平衡性和红黑性质。以下是实现插入功能的基本步骤：

1. **插入节点**：首先，将新节点以普通二叉搜索树的插入方式插入到树中。新节点的初始颜色设置为红色。

2. **修复红黑性质**：由于插入新节点可能会破坏红黑树的性质，因此需要进行调整。调整通常包括重新着色和进行旋转操作。

3. **保持树的平衡**：通过旋转和重新着色，确保树在插入操作后仍满足红黑性质。

下面是一个示例代码块，展示如何在红黑树中插入一个新节点：

// C语言伪代码示例
struct RBTreeNode {
    int data;
    enum Color color;  // 枚举类型：RED, BLACK
    struct RBTreeNode *left, *right, *parent;
};

// 函数原型声明
void insert(struct RBTreeNode **root, int data);
void fixViolation(struct RBTreeNode **root, struct RBTreeNode *z);

// 插入新节点的函数实现
void insert(struct RBTreeNode **root, int data) {
    // 创建新节点
    struct RBTreeNode *z = (struct RBTreeNode *)malloc(sizeof(struct RBTreeNode));
    z->data = data;
    z->color = RED;
    z->left = z->right = z->parent = NULL;

    // 插入节点，类似于二叉搜索树的插入
    struct RBTreeNode *y = NULL;
    struct RBTreeNode *x = *root;
    while (x != NULL) {
        y = x;
        if (z->data < x->data)
            x = x->left;
        else
            x = x->right;
    }
    z->parent = y;

    if (y == NULL)
        *root = z;
    else if (z->data < y->data)
        y->left = z;
    else
        y->right = z;

    // 插入修复红黑性质
    fixViolation(root, z);
}

### 3.1.2 插入过程中的颜色调整

在红黑树的插入操作中，当新节点的父节点是红色时，会破坏红黑树的性质，特别是性质4（从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点）。这时就需要进行颜色调整，以修复红黑性质。颜色调整主要包括两种情况：LL（左左）、LR（左右）、RR（右右）、RL（右左）旋转。

**LL旋转：** 当插入节点和其