数据结构进阶攻略：平衡二叉树与B树对决，深度剖析

# 1. 数据结构概述与二叉树基础

## 1.1 数据结构简介

在计算机科学中，数据结构是一门研究组织数据的方式，它包括了数据的逻辑结构、物理存储结构以及数据的操作与处理方法。一个良好的数据结构能够使数据更加容易存储、管理和检索，它直接关系到程序的效率和可扩展性。数据结构的类型包括数组、链表、堆、栈、队列、树和图等。

## 1.2 二叉树定义与特征

二叉树是数据结构中的一种基础类型，尤其在搜索树中扮演重要角色。它是由一组节点组成的层级结构，每个节点最多有两个子节点，分别是左子节点和右子节点。二叉树的特点使得其在查找、插入和删除数据时具有较高的效率。

## 1.3 二叉树的操作

二叉树的操作主要包括遍历、插入、删除和查找节点。遍历分为前序、中序、后序和层次遍历。插入和删除节点时需要注意保持二叉树的有序性，这直接影响到树的平衡性和效率。

// 二叉树节点的简单定义
class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    TreeNode(int value) {
        this.value = value;
        left = null;
        right = null;
    }
}

接下来章节将深入探讨平衡二叉树的原理与实现，为构建高效的搜索树奠定基础。

# 2. 平衡二叉树的原理与实现

在数据结构中，平衡二叉树是一种特殊形式的二叉搜索树，它在树的各个节点的平衡因子上做了限制，确保树保持一定的平衡状态。这样的树可以提供更优的查找性能，避免在最坏情况下退化成链表。本章节将深入解析平衡二叉树的原理，并探讨两种最常见的平衡二叉树——AVL树和红黑树。

## 2.1 平衡二叉树的概念解析

### 2.1.1 平衡二叉树的定义

平衡二叉树（Balanced Binary Tree），特别是指AVL树和红黑树，要求其所有的子树的高度差不超过1，这样可以保证操作的效率。平衡二叉树结构能够保证基本操作，如查找、插入、删除的时间复杂度保持在对数级别O(log n)。在这样的树中，任意节点的左子树与右子树的高度差被限制为不超过1。

### 2.1.2 平衡因子与平衡操作

平衡因子（Balance Factor）定义为该节点的左子树高度减去右子树高度。在平衡二叉树中，任何节点的平衡因子只能是-1、0或1。当平衡因子超过这个范围时，需要进行旋转操作来重新平衡树。

在AVL树和红黑树中，重新平衡树的策略有所不同。AVL树对平衡因子的限制更为严格，任何不平衡都需要通过旋转来修复。而红黑树通过维持其特有的颜色规则来保证树的平衡。

## 2.2 AVL树的原理与特性

### 2.2.1 AVL树的基本结构

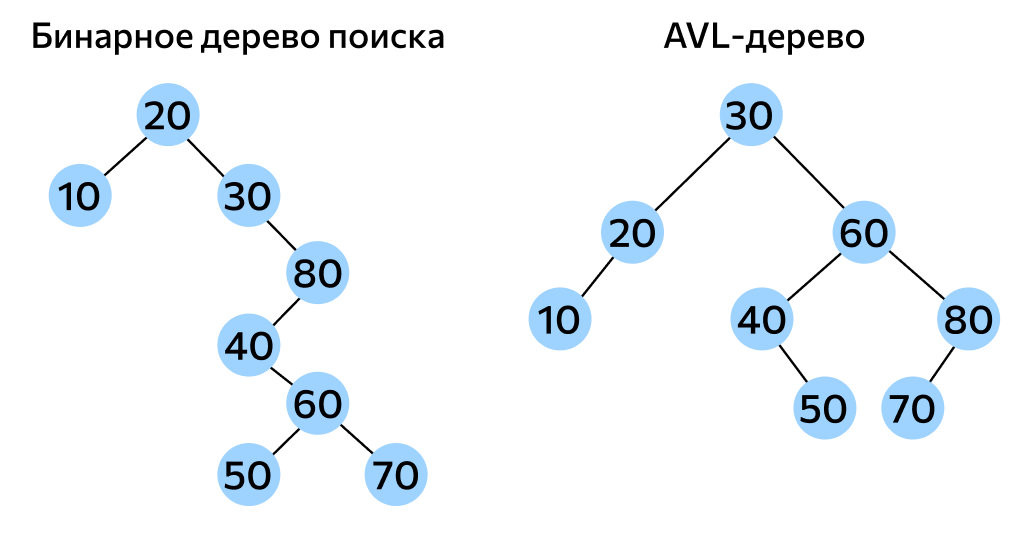
AVL树是一种高度平衡的二叉搜索树，任何节点的两个子树的高度最大差别为1。这种严格的高度平衡使得AVL树在查找操作时具有较高的效率。

AVL树的每个节点都维护了一个平衡因子，该平衡因子是左子树的高度减去右子树的高度。为了维持平衡性，AVL树定义了四种旋转操作：左旋（LL旋转）、右旋（RR旋转）、左右旋（LR旋转）和右左旋（RL旋转）。

### 2.2.2 AVL树的旋转操作

当插入或删除操作导致某个节点的平衡因子超出[-1, 0, 1]范围时，就需要进行相应的旋转操作来维持树的平衡。旋转操作会影响节点的父子关系，但不会破坏二叉搜索树的性质。

- **左旋（LL旋转）**：右子树过高，导致父节点的平衡因子为-2。需要将父节点向右上旋转，同时把右子节点提到父节点的位置。
- **右旋（RR旋转）**：左子树过高，导致父节点的平衡因子为2。需要将父节点向左上旋转，同时把左子节点提到父节点的位置。
- **左右旋（LR旋转）**：左子树的右子树过高，导致父节点的平衡因子为-2。需要先对左子节点做右旋操作，然后将父节点做左旋操作。
- **右左旋（RL旋转）**：右子树的左子树过高，导致父节点的平衡因子为2。需要先对右子节点做左旋操作，然后将父节点做右旋操作。

## 2.3 红黑树的原理与特性

### 2.3.1 红黑树的基本性质

红黑树是一种自平衡的二叉搜索树，它在节点中引入了额外的信息——颜色，且有以下五个性质：

1. 每个节点要么是红色，要么是黑色。
2. 根节点总是黑色。
3. 所有叶子节点（NIL节点，空节点）都是黑色。
4. 如果一个节点是红色，那么它的两个子节点都是黑色（不能有两个连续的红色节点）。
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

这五个性质确保了红黑树的平衡性。虽然它不像AVL树那样严格平衡，但其性质保证了最长路径不会超过最短路径的两倍，因此红黑树在插入和删除操作的性能上能够提供很好的保证。

### 2.3.2 红黑树的调整操作

红黑树的调整操作需要同时维护节点颜色和二叉搜索树的性质。当进行插入或删除操作后，可能需要进行以下几种调整：

- **变色**：在不违反红黑树五个性质的前提下，通过改变节点的颜色来重新平衡树。
- **左旋**：与AVL树中类似的左旋操作，用于调整树的结构。
- **右旋**：与AVL树中类似的右旋操作，用于调整树的结构。
- **重新着色并旋转**：在某些情况下，需要先进行变色，然后进行适当的旋转操作。

这些调整操作允许红黑树在插入和删除节点后，通过局部的重新平衡，迅速恢复到符合红黑树性质的状态。

# 3. B树的原理与应用

## 3.1 B树的定义与结构特点

### 3.1.1 多路平衡查找树的概念

B树是为磁盘或其他直接存取辅助存储设备设计的一种平衡查找树。它的设计思想是将尽可能多的键存放在一个节点中，从而减少树的高度，以便在磁盘上进行高效的查找、插入和删除操作。在B树中，一个节点可以包含更多的子节点，这取决于树的阶数（t），即节点可以包含的最大子节点数。每个节点包含的关键字数也比其子节点多一个，因此B树的节点关键字数范围为 `[t-1, 2t-1]`。

### 3.1.2 B树的节点与度

B树的节点结构是树中数据和树结构管理的关键。节点通常包含多个部分：

- 关键字（Key）：用于搜索和排序，节点中的关键字数目要满足特定的约束。
- 子指针（Children）：指向子节点，节点中的子指针数目比关键字数目多一个。
- 指示器（Indicator）：有时包含以指示子指针指向的子树中的关键码范围。

B树的一个关键特点是节点的最大度数（最大子节点数）和最小度数（最小子节点数）。最小度数 `t` 决定了B树的高度和存储效率。保持最小度数可以确保B树的平衡性，即所有叶子节点都在同一层。

### *.*.*.* 节点结构图示

为了更好地理解B树节点的构成，我们可以用一个简单的示意图来表示：

classDiagram
    class BTreeNode {
        <<interface>>