【希尔排序数学原理】：揭开排序算法背后的数学奥秘

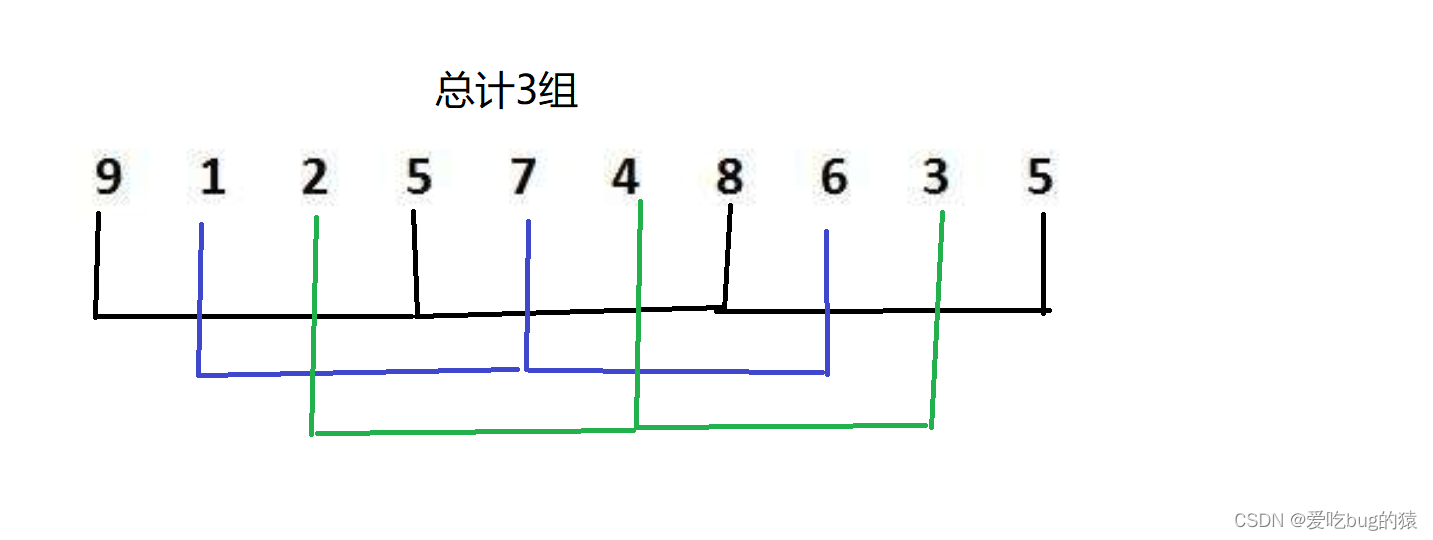
# 1. 希尔排序算法概述

希尔排序（Shell Sort），也称为递减增量排序算法，是插入排序的一种更高效的改进版本。它由Donald Shell于1959年提出，旨在解决直接插入排序在大规模数据集上的效率问题。希尔排序通过将原始数据分为多个子序列，并在这些子序列上分别执行插入排序，逐步减少子序列的间隔来达到整体排序的目的。这种方法极大地减少了大量数据的移动次数，尤其是在数据接近有序时，效率明显提高。

为了深入理解希尔排序的工作原理，我们先从其基本思想入手，再逐步探讨其数学基础、理论分析、优化策略以及与其他排序算法的比较，最后通过实际应用案例和未来发展趋势展望，展现希尔排序算法的强大生命力和广泛的适用场景。

graph LR
A[希尔排序算法概述] --> B[算法基本思想]
B --> C[间隔序列的优化]
C --> D[数学基础与理论分析]
D --> E[优化策略]
E --> F[与其他排序算法的比较]
F --> G[应用实例与展望]

在下一章中，我们将详细探讨希尔排序的数学基础，尤其是分组思想与间隔序列的选择标准，为理解其算法复杂度和效率优化奠定理论基础。

# 2. 希尔排序的数学基础

### 2.1 分组思想与间隔序列

#### 2.1.1 分组思想的提出与原理

在希尔排序的早期版本中，算法引入了一种称为“分组思想”的概念。这种思想基于将数组分为若干个子序列，每个子序列内的元素相互之间保持一定的间隔。初始时，这个间隔较大，随着排序过程的进行，这个间隔逐渐减小。通过这种间隔分组，希尔排序可以快速地将元素分布到大致正确的位置上，而后再通过更细粒度的比较和交换，达到最终的有序状态。

分组思想的原理在于利用插入排序对小数组操作效率高的特点，通过间隔序列逐步缩小分组，从而将插入排序的局部性优势最大化。这种策略在大数据集上比传统插入排序有了显著的性能提升，特别是在元素部分有序或分布有规律时。

#### 2.1.2 间隔序列的选择标准与数学证明

间隔序列的选择对希尔排序的性能至关重要。一个好的间隔序列应当满足以下标准：

- 应该从一个较大的数值开始，使得初步分组时能够将数据分布在一个较宽的范围，这有利于快速地消除较大范围内的不规则性。
- 随着算法的执行，间隔序列应该逐渐逼近1，这样可以保证算法最终达到完全有序状态。
- 数学证明表明，间隔序列需要满足`h_t ≡ 1 (mod 2)`和`h_t > h_{t+1} > 1`这两个条件，以确保间隔序列是递减的，并且间隔序列中的每个元素都能够与1互质。

经典的希尔排序间隔序列如`n/2`, `n/4`, ..., `1`或`3*2^{k-1}+1`等都是满足上述标准的例子。

### 2.2 数论在希尔排序中的应用

#### 2.2.1 素数间隔序列的优化

研究者们发现使用素数作为间隔序列的起始值，能够进一步提升希尔排序的性能。素数间隔序列之所以有效，是因为它们在数值上的随机性较强，这种随机性有助于避免数据分布的特定规律性干扰排序过程。一个著名的素数间隔序列是由Hibbard提出的`2^k - 1`序列，例如`1, 3, 7, 15, ...`。

然而，使用素数间隔序列也存在缺点，当处理特定类型的数据时，可能会导致性能退化。因此，对于间隔序列的选择，仍然存在许多研究空间和优化机会。

#### 2.2.2 数论原理在算法效率中的作用

在希尔排序中，数论的原理不仅可以指导间隔序列的选择，还可以用来分析算法的效率。例如，使用素数间隔序列的希尔排序算法，其时间复杂度的分析可以通过数论中的模运算和素数分布的性质来进行。数学上，这种分析能够帮助我们理解算法在不同情况下的行为，并为改进算法提供理论基础。

数论中的一些定理和结论，如欧拉函数、费马小定理等，在希尔排序的理论分析中也可能会找到应用。通过这些工具，我们可以更深入地理解间隔序列对排序过程的影响，以及如何设计更高效的间隔序列来优化希尔排序的性能。

# 3. 希尔排序的理论分析

希尔排序（Shell Sort）是插入排序的一种更高效的改进版本，由Donald Shell在1959年提出。这种算法通过将原始数据分成若干个子序列，分别进行直接插入排序，从而达到整个序列基本有序的目的。之后，再对全体记录进行一次直接插入排序。

## 3.1 算法时间复杂度分析

### 3.1.1 最坏情况与平均情况分析

希尔排序的时间复杂度在最坏情况下是O(n^2)，这是因为虽然通过分组排序可以减少单次排序的比较次数，但在最坏的情况下，每次分组排序并没有显著地减少整体的比较和移动次数。然而，在数据接近有序时，希尔排序的效率会接近O(nlogn)，这是其相较于基本插入排序的优势所在。

在平均情况下，希尔排序的时间复杂度同样难以精确计算，因为它受到间隔序列选择的影响。研究表明，对于好的间隔序列，平均情况下的时间复杂度接近O(n^(3/2))到O(n^(4/3))。

### 3.1.2 时间复杂度的数学推导

推导希尔排序的时间复杂度需要深入研究其间隔序列的选择方式以及插入排序在不同间隔下的性能。对于间隔序列h_t、h_(t-1)、...、h_1，其中h_t是数组长度n的某个子序列的间隔，对于每个间隔i，算法都要执行一次插入排序。

通过数学分析，我们可以得出对于间隔为i的插入排序，其性能主要受制于数组中逆序对的数量。在希尔排序中，由于数组被分成多个子序列，每个子序列的大小为n/i，因此算法的总比较次数是子序列内比较次数的总和。

当间隔序列选择为1时，希尔排序退化为普通的插入排序，而当间隔序列合理选择时，最终的比较次数会大大减少。数学推导的关键在于理解不同间隔下逆序对数量与比较次数的关系，以及间隔序列对总体性能的影响。

## 3.2 算法稳定性和比较次数

### 3.2.1 稳定性的数学定义及其重要性

稳定性在排序算法中是一个重要属性，它指的是相等的元素在排序后保持原有相对顺序。在希尔排序中，由于使用了插入排序的子过程，这个子过程是稳定的。但是由于数据在不同间隔的多个子序列中进行排序，最终稳定性可能会受到影响。

理论上，如果一个排序算法在所有间隔下的子排序过程中都是稳定的，那么整个希尔排序算法也是稳定的。然而，在实践中，由于多轮排序过程中元素位置的多次变动，很难保证算法的稳定性，特别是在间隔选择不当的情况下。

### 3.2.2 实际比较次数与理论最小值的比较

尽管希尔排序不是稳定的，但它在比较次数上具有优势，尤其是在间隔选择得当时。对于给定的间隔序列，实际比较次数与理论最小值的差异是衡量算法性能的一个重要指标。通过实验和分析，我们可以了解在不同大小的数组中，希尔排序所需的比较次数。

使用间隔序列h_t、h_(t-1)、...、h_1时，每次分组排序的比较次数会随着间隔的减小而增加，因为子序列的元素数量在增加。理论上的最小值是基于数据完全随机分布的假设，但实际应用中数据往往并非完全随机，因此实际比较次数可能会少于理论最小值。

在对希尔排序进行理论分析时，我们还必须考虑最坏情况、平均情况和最好情况（即当输入数组已经基本有序时）下的性能表现。通过分析这些不同情况下的比较次数，我们能够更全面地评估希尔排序的效率和适用场景。

> 注：本章节内容继续展开，会详细探讨希尔排序的稳定性和比较次数的深入分析，包括各种间隔序列选择对性能的影响，以及实际应用中的性能评估。后续内容将逐渐深入，提供对希尔排序更全面的理解。

# 4. 希尔排序的优化策略

## 4.1 动态间隔序列的选择

### 4.1.1 基于数据分布的间隔序列调整

希尔排序算法的一个主要优化点是动态地调整间隔序列，从而适应不同的数据分布，提高排序效率。在传统的希尔排序中，初始间隔序列通常是按照某个固定的比例选取的，但这种方法并不总是最有效的，尤其是当数据具有某种特定模式时。

为了适应数据的分布，我们可以设计一种策略，该策略在排序过程中根据数据的特性动态调整间隔序列。一种常见的方法是根据数据的比较和交换次数来调整间隔序