希尔排序的并行潜力：多核处理器优化的终极指南

# 1. 希尔排序算法概述

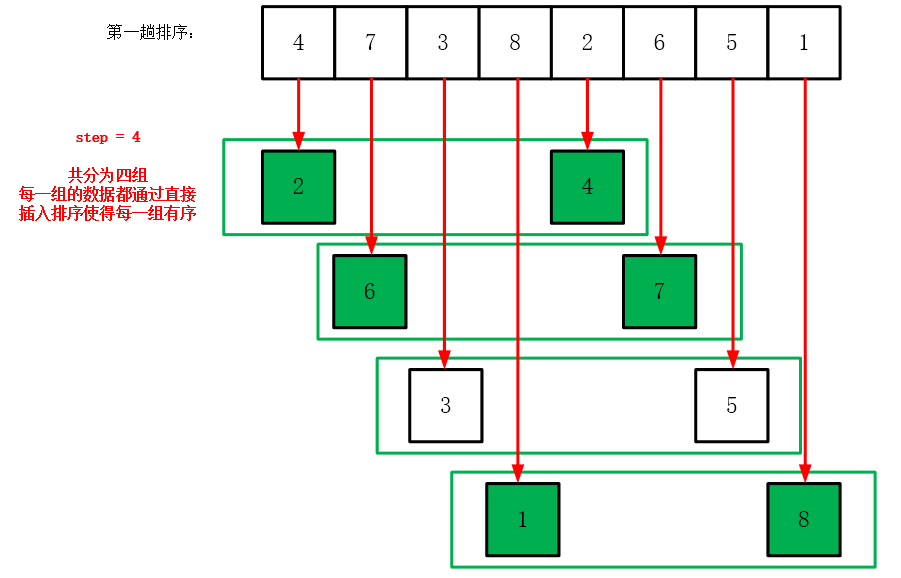
希尔排序算法，作为插入排序的一种更高效的改进版本，它是由数学家Donald Shell在1959年提出的。希尔排序的核心思想在于先将整个待排序的记录序列分割成若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行一次直接插入排序。这样的方式大大减少了记录的移动次数，从而提升了算法的效率。

## 1.1 希尔排序的起源与发展
希尔排序算法的提出，旨在解决当时插入排序在处理大数据量时效率低下的问题。自从提出后，该算法经过了多次改进和发展，其在某些情况下甚至优于快速排序等更复杂的排序算法。

## 1.2 希尔排序的适用场景
希尔排序适合于中等大小的数据集排序，特别是当数据集接近有序时，希尔排序表现得尤为出色。这种排序算法也常用于嵌入式系统和硬件驱动程序中，因为其算法复杂度较低且代码较为简洁。

接下来章节将深入分析希尔排序算法的原理，同时探讨如何将希尔排序并行化，并展示该算法在现代并行计算环境中的应用和优化。

# 2. 并行计算基础与希尔排序的并行化

## 2.1 并行计算理论基础
### 2.1.1 多核处理器架构简介
在本部分，我们将讨论多核处理器架构的基础知识。多核处理器是由两个或更多的独立处理核心组成，每个核心都有自己的算术逻辑单元、寄存器和缓存。这允许同时处理多个计算任务，大幅度提升了计算机处理数据的能力。

核心之间通过共享的总线或者专门的互联网络进行通信，以同步或交换数据。每个核心可以看作是独立的处理器，可以运行独立的线程或进程，也可以并行执行相同的任务以提高性能。

近年来，由于摩尔定律的放缓和功耗限制，主流处理器架构逐渐从提高单核心频率转向增加核心数量，因此多核架构成为了提高处理器性能的主要途径。

### 2.1.2 并行计算的优势与挑战
并行计算利用多核处理器的能力，通过多个处理器同时工作来解决计算问题，其优势显而易见：
- **提高速度**：通过并行处理，可以显著减少计算时间。
- **资源扩展**：并行计算允许使用更多资源来处理更大的数据集。
- **高可用性**：计算任务可以分布到多个处理器，提高了系统处理故障的能力。

然而，并行计算同样面临着挑战：
- **同步问题**：处理核心之间需要同步协调，以避免数据不一致。
- **负载均衡**：合理分配任务到各个处理核心，确保资源不被浪费。
- **内存访问优化**：并行系统中内存访问问题可能导致性能瓶颈。

接下来的章节将探讨如何将希尔排序算法并行化，以应对并行计算带来的挑战，并充分利用其优势。

## 2.2 希尔排序算法原理
### 2.2.1 希尔排序的基本步骤和性能特点
希尔排序是插入排序的一种改进版本，通过引入“间隔”概念来提高排序效率。基本步骤如下：

1. 初始化一个间隔序列，如 `n/2`, `n/4`, ..., `1`，其中 `n` 是待排序数组的长度。
2. 对每个间隔，使用插入排序算法对相应位置的元素进行排序。
3. 随着间隔的减少，逐渐缩小间隔直至为1，此时算法退化成普通的插入排序，数组已排序完成。

希尔排序的性能特点：
- **平均时间复杂度**：介于O(n log n)到O(n^(3/2))之间，这取决于间隔序列的选择。
- **空间复杂度**：O(1)，希尔排序是原地排序算法。
- **稳定性**：不稳定排序，相同值的元素可能会被交换位置。

与其他排序算法相比，希尔排序的优点在于简单且适用于链表排序，缺点是平均性能无法与快速排序或归并排序等高效算法相比。

### 2.2.2 希尔排序与其他排序算法的比较
为了更深入理解希尔排序，我们将与其他排序算法进行比较：

- **快速排序**：平均时间复杂度为O(n log n)，快速排序比希尔排序更快，但需要额外的空间来存储栈，并且稳定性较差。
- **归并排序**：归并排序同样具有O(n log n)的时间复杂度，但也是非原地排序，需要额外的内存空间。
- **堆排序**：具有O(n log n)的时间复杂度，是原地排序，但同样不稳定。
- **冒泡排序**：平均和最坏情况都是O(n^2)，希尔排序优于冒泡排序，尤其是当数组较大时。

通过比较可以发现，希尔排序在小规模数据集或者对于链表排序是一个不错的选择，但在处理大规模数据集时，可能不如快速排序或归并排序高效。

## 2.3 希尔排序的并行化策略
### 2.3.1 数据分割与任务分配方法
为了实现希尔排序的并行化，首先需要解决数据分割和任务分配的问题。数据分割方法通常依赖于数组的大小以及可用的处理核心数量。一个简单的策略是将数组平均分成若干部分，每部分对应一个核心。

一种有效的方法是基于间隔的分割。例如，对于间隔序列 `gap1, gap2, ..., gapk`，每个核心可以负责一个间隔的所有元素排序。核心1负责间隔 `gap1` 的所有元素排序，核心2负责间隔 `gap2` 的，依此类推。

### 2.3.2 并行希尔排序的设计与实现
设计并行希尔排序算法需要注意以下几点：

1. **初始数据分割**：将数组均匀分割到不同的处理核心。
2. **局部排序**：每个核心执行局部希尔排序，利用现有的顺序局部性。
3. **间隙缩减**：当间隙缩小到1时，进行全局排序，此时所有核心协作完成最终排序。

实现并行希尔排序的代码示例如下：

def parallel希尔排序(data, num_cores):
    gaps = compute_gaps(len(data)) # 计算间隔序列
    # 数据分配给不同的线程或处理器核心
    segments = divide_data(data, num_cores)

    # 每个核心并行执行局部希尔排序
    parallel_sort(segments, gaps, num_cores)

    # 合并已排序的数据段并执行全局希尔排序
    sorted_data = merge_segments(segments)
    return sorted_da