希尔排序的适用范围：局限性与场景选择的专家建议

# 1. 希尔排序算法概述

希尔排序算法是一种高效的插入排序改进版本，由计算机科学家Donald Shell在1959年提出。它通过将原始数据集分组，然后对分组内的元素进行插入排序，逐步减小组间距（步长），最终在步长为1时完成整个数据集的排序。希尔排序旨在通过这种分组方式减少数据移动的次数，从而提高排序效率，特别适合中等大小的数据集排序。这种方法既保留了插入排序的优点，又能更好地处理大规模的数据集。尽管希尔排序在最坏情况下的时间复杂度仍然是O(n^2)，但其平均性能表现却能与许多更复杂的算法相媲美。

# 2. 希尔排序的内部工作原理

希尔排序是基于插入排序的一种排序算法，由Donald Shell于1959年提出。不同于传统插入排序的局限性，希尔排序通过将原始数据分为若干子序列进行插入排序，以此减少数据移动次数，提高效率。接下来我们将详细探讨希尔排序的内部工作原理。

## 2.1 希尔排序的步骤解析

### 2.1.1 初始步长的选择

希尔排序的性能在很大程度上取决于步长序列的选择。初始步长是步长序列的第一个元素，它的选取对算法效率有直接影响。一般情况下，初始步长的选择与待排序数组的大小有关，常见方法是将其取为数组长度的一半。

def shell_sort(arr):
    n = len(arr)
    gap = n // 2  # 初始步长设为数组长度的一半
    # 对每个步长进行插入排序
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            # 插入排序，使用当前步长
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap //= 2  # 缩小步长

代码逻辑逐行解读分析：
- 代码首先获取数组的长度，并设定初始步长为数组长度的一半。
- 外层循环控制步长的递减，从初始步长开始逐步减小。
- 内层循环是一个基于当前步长的插入排序，它将数组分为若干子序列。
- 在内层循环中，如果当前元素小于其对应步长位置的元素，则将后者向后移动，直到找到合适的位置插入当前元素。
- 每完成一轮内层循环后，步长减半，进行下一轮插入排序，直至步长为0。

### 2.1.2 插入排序的变种应用

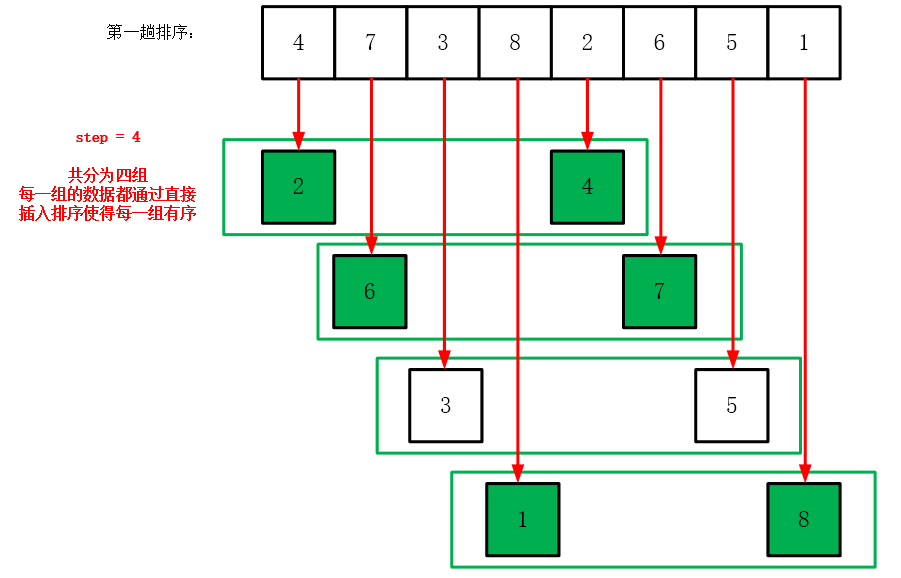
希尔排序实质上是对传统的插入排序进行了优化，它通过分组的方式降低了数据移动的次数。这种方法可以理解为将待排序数组分割成多个子序列，每个子序列分别进行插入排序，子序列的数量由初始步长决定。

表格展示不同步长下的插入排序情况：

| 步长 | 插入排序情况 |
| ---- | ------------ |
| n/2 | 第一次排序后 |
| n/4 | 第二次排序后 |
| ... | ... |
| 1 | 最后一次排序 |

在这个表格中，我们可以看到随着步长的减小，数组被细分成越来越多的组，最终在步长为1时，整个数组作为一组进行最终的插入排序。

## 2.2 希尔排序的数学分析

### 2.2.1 时间复杂度的理论推导

希尔排序的时间复杂度并不像传统排序算法那样容易计算，因为它依赖于步长序列的选择。然而，通过理论推导和实验分析，我们可以得知希尔排序的平均时间复杂度介于O(nlogn)到O(n^2)之间。具体时间复杂度会随着步长序列的不同而有所变化。

### 2.2.2 空间复杂度及稳定性分析

希尔排序是一个原地排序算法，不需要额外的存储空间，其空间复杂度为O(1)。在稳定性方面，希尔排序不是稳定的排序方法，因为在执行插入排序的过程中可能会出现相同的元素之间位置的相对顺序被改变。

mermaid格式流程图描述希尔排序过程：

flowchart TD
    A[开始希尔排序] --> B[选择初始步长]
    B --> C[执行插入排序]
    C --> D[步长除二]
    D -->|步长大于零| C
    D -->|步长为零| E[结束排序]

流程图简单概括了希尔排序的整个过程。从选择初始步长开始，然后进行一轮插入排序，接着将步长除以二，重复插入排序过程直到步长变为零，排序完成。

# 3. 希尔排序的实际应用场景

## 3.1 小规模数据集的排序

### 3.1.1 与传统排序算法的对比

希尔排序之所以在小规模数据集上具有一定的优势，是由于其插入排序的变种特性，在部分有序的序列上表现尤为出色。相比之下，传统的插入排序算法仅当数据已经基本有序时才能展现出较好的性能，而希尔排序通过设置步长序列，使得数据在更粗粒度上进行排序，从而减少了比较和交换的次数。

在对比希尔排序和传统的快速排序（Quick Sort）算法时，我们发现，快速排序在平均情况下的时间复杂度为O(n log n)，但其常数因子较大，并且在最坏情况下的时间复杂度为O(n^2)。而在小规模数据集上，希尔排序虽然平均时间复杂度不如快速排序，但由于其较低的常数因子和较低的交换次数，实际上它能够以更快的速度完成排序。

### 3.1.2 效率提升的实际案例

为了直观展示希尔排序在小规模数据集上的效率提升，我们可以通过一个具体的例子来演示。假设我们有一个包含100个元素的小数组，我们将使用希尔排序和插入排序对它进行排序，并记录两者所用的时间。

以下是使用希尔排序对数组进行排序的Python代码示例：

def shell_sort(arr):
    n = len(arr)
    gap = n // 2
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while j >=