MATLAB曲线平滑与声学：平滑声音数据，提升音质

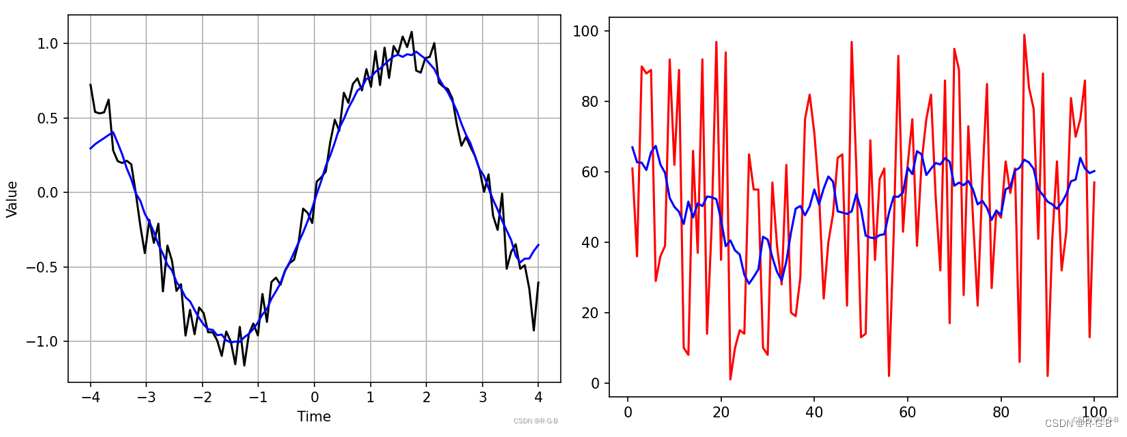
# 1. MATLAB曲线平滑基础**

MATLAB曲线平滑是一种技术，用于减少数据中的噪声和异常值，从而获得更平滑和更具代表性的曲线。它在各种领域都有广泛的应用，包括信号处理、图像处理和数据分析。

曲线平滑的基本原理是使用数学算法来创建平滑曲线，该曲线与原始数据拟合，同时滤除噪声和异常值。MATLAB提供了各种曲线平滑技术，每种技术都有其独特的优点和缺点。

在选择曲线平滑技术时，需要考虑几个因素，包括数据的类型、噪声水平以及所需的平滑程度。在本章中，我们将讨论MATLAB中常用的曲线平滑技术，并探讨其原理、实现和应用。

# 2. MATLAB曲线平滑技术

### 2.1 移动平均法

#### 2.1.1 原理和实现

移动平均法是一种简单的曲线平滑技术，它通过计算数据点在特定窗口内的平均值来平滑数据。窗口的大小由窗口宽度参数 `span` 指定。

% 输入数据
data = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];

% 移动平均平滑，窗口宽度为 3
span = 3;
smoothed_data = movmean(data, span);

% 绘制原始数据和平滑数据
figure;
plot(data, 'b', 'LineWidth', 2);
hold on;
plot(smoothed_data, 'r', 'LineWidth', 2);
legend('原始数据', '平滑数据');
xlabel('样本点');
ylabel('值');
title('移动平均平滑');

#### 2.1.2 参数选择和影响

窗口宽度 `span` 是移动平均法的关键参数。较大的窗口宽度会产生更平滑的曲线，但可能会损失细节。较小的窗口宽度会保留更多细节，但平滑效果可能不够。

### 2.2 Savitzky-Golay滤波

#### 2.2.1 原理和实现

Savitzky-Golay滤波是一种基于最小二乘拟合的多项式平滑技术。它通过将数据点拟合到一个多项式函数来平滑数据，然后使用拟合函数来计算平滑后的值。

% 输入数据
data = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];

% Savitzky-Golay滤波，窗口宽度为 5，多项式阶数为 2
window_size = 5;
polyorder = 2;
smoothed_data = sgolayfilt(data, polyorder, window_size);

% 绘制原始数据和平滑数据
figure;
plot(data, 'b', 'LineWidth', 2);
hold on;
plot(smoothed_data, 'r', 'LineWidth', 2);
legend('原始数据', '平滑数据');
xlabel('样本点');
ylabel('值');
title('Savitzky-Golay滤波');

#### 2.2.2 窗口大小和多项式阶数的选择

窗口大小和多项式阶数是 Savitzky-Golay滤波的关键参数。较大的窗口大小会产生更平滑的曲线，但可能会损失细节。较高的多项式阶数会产生更精确的拟合，但可能会引入振荡。

### 2.3 小波分解与重构

#### 2.3.1 小波分解原理

小波分解是一种将信号分解为一系列小波系数的技术。小波是一种具有局部化时频特性的小型波形。通过使用不同尺度的滤波器组对信号进行分解，可以获得不同频率范围的小波系数。

#### 2.3.2 小波重构与平滑

小波重构是将小波系数重新组合成平滑信号的过程。通过选择保留特定频率范围的小波系数，可以实现对信号的平滑。

% 输入数据
data = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];

% 小波分解，使用 Daubechies 4 小波
wavelet = 'db4';
[cA, cD] = dwt(data, wavelet);

% 小波重构，保留近似系数
reconstructed_data = idwt(cA, [], wavelet);

% 绘制原始数据和平滑数据
figure;
plot(data, 'b', 'LineWidth', 2);
hold on;
plot(reconstructed_data, 'r', 'LineWidth', 2);
legend('原始数据', '平滑数据');
xlabel('样本点');
ylabel('值');
title('小波分解与重构');

# 3.1 声音数据预处理

**3.1.1 去噪**

声音数据中不可避免地存在噪声和干扰，这些噪声会影响后续的平滑和分析。因此，在进行曲线平滑之前，必须对声音数据进行去噪处理。常用的去噪方法包括：

- **中值滤波：**中值滤波是一种非线性滤波器，它通过计算数据窗口内所有样本的中值来替换窗口中心样本。中值