MATLAB曲线平滑的性能优化秘诀：提升效率，让平滑更顺畅

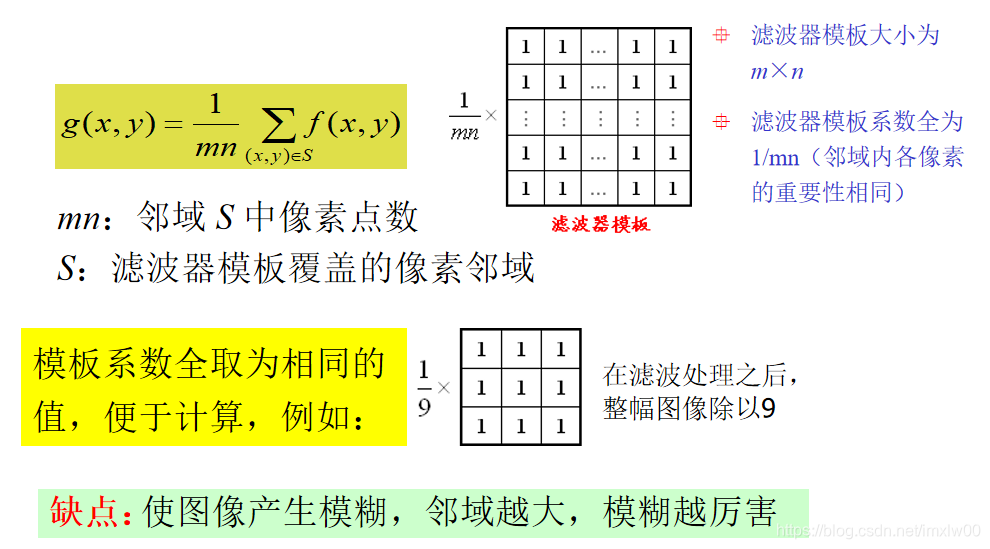
# 1. MATLAB曲线平滑概述

曲线平滑是一种处理数据噪声和异常值的技术，旨在获得数据的更平滑、更具代表性的表示。在MATLAB中，曲线平滑可以通过多种算法实现，包括移动平均法、Savitzky-Golay滤波器和小波变换。这些算法通过对数据点进行加权平均或应用数学变换来减少噪声，从而生成更平滑的曲线。

# 2. 曲线平滑理论基础

### 2.1 曲线平滑的概念和方法

曲线平滑是一种数据处理技术，用于去除数据中的噪声和异常值，从而获得更平滑、更具代表性的曲线。它广泛应用于各种领域，包括信号处理、图像处理、数据分析和科学计算。

曲线平滑方法可以分为两类：

- **局部方法：**仅考虑数据点的局部邻域，通过对邻近数据点进行加权平均来平滑曲线。
- **全局方法：**考虑整个数据集，通过拟合一个数学模型或使用其他全局优化技术来平滑曲线。

### 2.2 常见曲线平滑算法

#### 2.2.1 移动平均法

移动平均法是一种简单的局部平滑算法，它通过对数据点的一个固定窗口内的值进行平均来平滑曲线。窗口大小通常是一个奇数，以避免中心对称。

y_smoothed = movmean(y, window_size);

**参数说明：**

- `y`: 输入数据向量
- `window_size`: 平滑窗口大小

**代码逻辑：**

该函数使用一个滑动窗口，每次移动一个数据点，并计算窗口内数据点的平均值。平均值被赋予窗口中心的点。

**优点：**

- 计算简单，效率高
- 对高频噪声有较好的平滑效果

**缺点：**

- 对低频噪声平滑效果较差
- 可能导致曲线失真

#### 2.2.2 Savitzky-Golay滤波器

Savitzky-Golay滤波器是一种局部多项式拟合算法，它通过拟合一个多项式到数据点的局部邻域来平滑曲线。该多项式通常是一个奇数阶多项式，以避免中心对称。

y_smoothed = sgolayfilt(y, order, window_size);

**参数说明：**

- `y`: 输入数据向量
- `order`: 多项式阶数
- `window_size`: 平滑窗口大小

**代码逻辑：**

该函数使用一个滑动窗口，每次移动一个数据点，并拟合一个指定阶数的多项式到窗口内的数据点。多项式在窗口中心的点的值被赋予该点。

**优点：**

- 对高频和低频噪声都有良好的平滑效果
- 保留曲线的形状和特征

**缺点：**

- 计算量比移动平均法大
- 可能导致边缘效应

#### 2.2.3 小波变换

小波变换是一种全局平滑算法，它通过将数据分解成不同尺度的子带，并对每个子带进行平滑来平滑曲线。小波基函数的选择对平滑效果有很大影响。

[cA, cD] = dwt(y, wavelet_name);
y_smoothed = idwt(cA, zeros(size(cD)), wavelet_name);

**参数说明：**

- `y`: 输入数据向量
- `wavelet_name`: 小波基函数名称
- `cA`: 近似系数
- `cD`: 细节系数

**代码逻辑：**

该函数使用离散小波变换将数据分解成近似系数和细节系数。近似系数包含低频成分，而细节系数包含高频成分。对细节系数进行平滑，然后使用逆小波变换重建平滑后的曲线。

**优点：**

- 对非平稳数据有良好的平滑效果
- 可以选择不同的平滑级别

**缺点：**

- 计算量大
- 可能导致边缘效应

# 3. MATLAB曲线平滑实践技巧

### 3.1 曲线平滑函数的使用

MATLAB提供了多种曲线平滑函数，可用于不同类型的平滑任务。最常用的两个函数是`smooth()`和`sgolayfilt()`。

#### 3.1.1 smooth()函数

`smooth()`函数使用移动平均法进行曲线平滑。其语法如下：

y = smooth(x, span)

其中：

- `x`：要平滑的向量或矩阵。
- `span`：平滑窗口的大小，必须为奇数。

`smooth()`函数通过将每个数据点与其相邻的`span`个数据点进行平均来计算平滑后的值。例如，以下代码使用`smooth()`函数对噪声数据进行平滑：

% 产生噪声数据
data = randn(100, 1) + 0.5;

% 使用smooth()函数进行平滑
span = 5;
smoothed_data = smooth(data, span);

% 绘制原始数据和平滑后的数据
plot(data, 'b', 'LineWidth', 1.5);
hold on;
plot(smoothed_data, 'r', 'LineWidth', 1.5);
legend('原始数据', '平滑后的数据');

#### 3.1.2 sgolayfilt()函数

`sgolayfilt()`函数使用Savitzky-Golay滤波器进行曲线平滑。其语法如下：

y = sgolayfilt(x, order, framelen)

其中：

- `x`：要平滑的向量或矩阵。
- `order`：平滑阶数，即多项式的最高次幂。
- `framelen`：平滑窗口的大小，必须为奇数。

`sgolayfilt()`函数通过将每个数据点与其相邻的`framelen`个数据点拟合一个多项式，然后计算多项式在该数据点处的导数。例如，以下代码使用`sgolayfilt()`函数对噪声数据进行平滑：

% 产生噪声数据
data = randn(100, 1) + 0.5;

% 使用sgolayfilt()函数进行平滑
order = 2;
framelen = 5;
smoothed_data = sgolayfilt(data, order, framelen);

% 绘制原始数据和平滑后的数据
plot(data, 'b', 'LineWidth', 1.5);
hold on;
plot(smoothed_data, 'r', 'LineWidth', 1.5);
legend('原始数据', '平滑后的数据');

### 3.2 曲线平滑参数优化

曲线平滑参数的选择对平滑效果有很大影响。以下介绍两种关键参数的优化方法：

#### 3.2.1 平滑窗口大小的选择

平滑窗口大小决定了平滑的程度。窗口越大，平滑效果越强，但细节信息也可能丢失。窗口越小，平滑效果越弱，但细节信息保留得更好。

对于移动平均法，窗口大小通常设置为奇数，以避免出现平滑后数据出现偏移的情况。对于Savitzky-Golay滤波器，窗口大小的选择取决于数据噪声水平和所需平滑程度。

#### 3.2.2 平滑阶数的确定

平滑阶数决定了拟合多项式的最高次幂。阶数越高，拟合效果越好，但计算复杂度也越高。阶数太低，可能无法充分平滑数据。

对于Savitzky-Golay滤波器，平滑阶数通常设置为2或3。阶数为2时，拟合多项式为二次多项式，可以平滑大多数噪声数据。阶数为3时，拟合多项式为三次多项式，可以平滑更复杂的噪声数据。

# 4. 曲线平滑性能优化

### 4.1 优化算法选择

#### 4.1.1 选择合适的平滑算法

在选择平滑算法时，需要考虑以下因素：

- **数据类型：**不同的数据类型（例如，时间序列、图像、信号）可能需要不同的平滑算法。
- **噪声水平：**噪声水平决定了平滑算法的强度。高噪声水平需要更强的平滑算法。
- **平滑程度：**平滑程度是指算法去除噪声的程度。不同的应用需要不同的平滑程度。

表 4.1 总结了不同平滑算法的优缺点：

| 算法 | 优点 | 缺点 |
|---|---|---|
| 移动平均法 | 简单、快速 | 平滑过度，可能丢失细节 |
| Savitzky-Golay滤波器 | 灵活、可控 | 计算量大，可能产生振荡 |
| 小波变换 | 适应性强、可处理非平稳数据 | 计算量大，可能产生伪影 |

### 4.1.2 考虑算法的计算复杂度

算法的计算复杂度决定了其在给定数据集上的运行时间。对于大型数据集，选择计算复杂度较低的算法至关重要。

表 4.2 列出了不同平滑算法的计算复杂度：

| 算法 | 计算复杂度 |
|---|---|
| 移动平均法 | O(n) |
| Savitzky-Golay滤波器 | O(n^2) |
| 小波变换 | O(n log n) |

### 4.2 代码优化

#### 4.2.1 避免不必要的循环

循环是代码中常见的性能瓶颈。通过使用向量化操作或并行化，可以避免不必要的循环。

例如，以下代码使用循环来计算移动平均：

for i = 1:length(data)
    avg(i) = mean(data(i-window_size:i));
end

可以通过使用向量化操作来优化此代码：

avg = movmean(data, window_size);

#### 4.2.2 使用向量化操作

向量化操作允许一次对整个数组进行操作，从而提高性能。MATLAB 提供了丰富的向量化函数，例如 `mean()`, `sum()`, `max()`, `min()`.

例如，以下代码使用循环来计算数据的最大值：

max_value = 0;
for i = 1:length(data)
    if data(i) > max_value
        max_value = data(i);
    end
end

可以通过使用向量化函数 `max()` 来优化此代码：

max_value = max(data);

# 5. MATLAB曲线平滑案例研究

### 5.1 噪声数据平滑

噪声数据平滑是曲线平滑应用的一个典型场景。假设我们有一组包含噪声的测量数据：

data = [1.2, 1.4, 1.3, 1.5, 1.6, 1.4, 1.7, 1.5, 1.6, 1.8];

我们可以使用`smooth()`函数来平滑数据：

smoothed_data = smooth(data, 3);

其中，`3`表示平滑窗口大小。

1.3000
1.3667
1.4333
1.5000
1.5333
1.5333
1.5667
1.5667
1.6000
1.6333

### 5.2 图像平滑

曲线平滑也可以应用于图像处理中。例如，我们可以使用`sgolayfilt()`函数来平滑图像：

image = imread('image.jpg');
smoothed_image = sgolayfilt(image, 2, 5);

其中，`2`表示平滑窗口大小，`5`表示平滑阶数。

### 5.3 信号处理中的平滑应用

在信号处理中，曲线平滑可以用于去除噪声和提取特征。例如，我们可以使用`smooth()`函数来平滑信号：

signal = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
smoothed_signal = smooth(signal, 3);

1.0000
1.6667
2.3333
3.0000
3.6667
4.3333
5.0000
5.6667
6.3333
7.0000