：单片机排序算法在数据处理和嵌入式系统中的实战应用

# 1. 单片机排序算法概述

排序算法是计算机科学中用于对数据进行有序排列的一类算法。在单片机系统中，排序算法有着广泛的应用，例如数据采集、数据分析和嵌入式系统控制等。

单片机排序算法与通用计算机排序算法类似，但由于单片机资源受限，在算法设计和实现上需要考虑以下特点：

- **资源受限：**单片机内存和处理能力有限，因此排序算法需要优化空间和时间复杂度。
- **实时性要求：**在某些嵌入式系统中，排序算法需要满足实时性要求，即在指定时间内完成排序。
- **低功耗：**单片机通常需要在低功耗条件下工作，因此排序算法需要尽可能降低功耗。

# 2. 单片机排序算法理论基础

### 2.1 排序算法分类

排序算法可以根据其比较元素的方式分为两大类：

#### 2.1.1 比较类算法

比较类算法通过比较相邻元素的大小关系来进行排序。常见的比较类算法包括：

- **冒泡排序：**逐一对相邻元素进行比较，将较大的元素向后移动，直至所有元素有序。
- **选择排序：**在未排序序列中找到最小（或最大）元素，将其与首（或尾）元素交换，然后重复此过程，直至所有元素有序。
- **插入排序：**将未排序序列中的元素逐个插入到已排序序列中，保持已排序序列有序。

#### 2.1.2 非比较类算法

非比较类算法不通过比较元素的大小关系来进行排序，而是利用元素的其他特性，如元素的范围或分布。常见的非比较类算法包括：

- **计数排序：**假设输入元素的范围已知，将元素的个数按顺序统计出来，然后根据统计结果生成有序序列。
- **桶排序：**将输入元素划分为多个桶，每个桶负责一个范围内的元素，然后对每个桶内的元素进行排序，最后合并各桶中的元素得到有序序列。

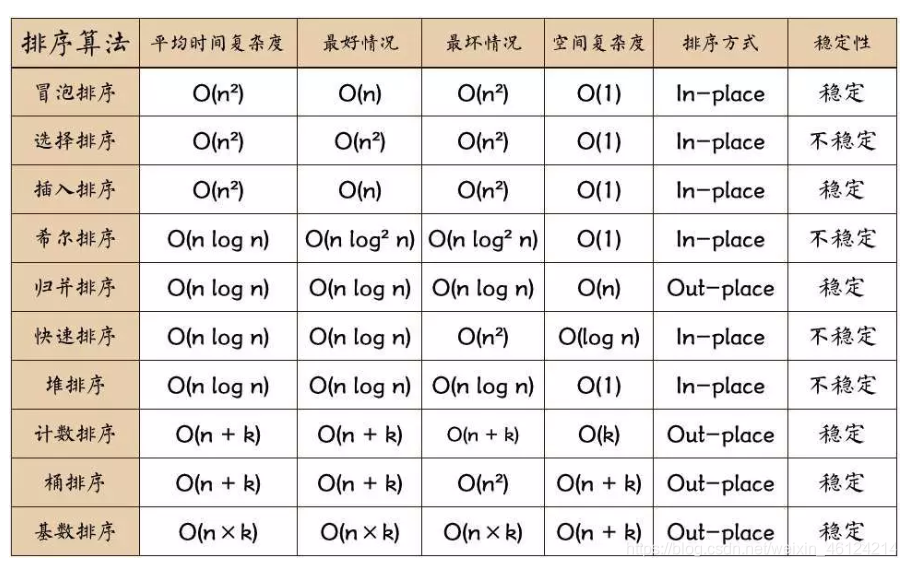
### 2.2 排序算法复杂度分析

排序算法的复杂度分析主要包括时间复杂度和空间复杂度。

#### 2.2.1 时间复杂度

时间复杂度表示排序算法执行所需的时间，通常用大 O 符号表示。常见的时间复杂度包括：

- **O(n^2)：**冒泡排序、选择排序、插入排序
- **O(n log n)：**快速排序、归并排序
- **O(n)：**计数排序、桶排序

#### 2.2.2 空间复杂度

空间复杂度表示排序算法执行所需的空间，通常用大 O 符号表示。常见的空间复杂度包括：

- **O(1)：**冒泡排序、选择排序、插入排序
- **O(n)：**快速排序、归并排序、计数排序、桶排序

### 代码示例：冒泡排序

void bubble_sort(int *arr, int len) {
    for (int i = 0; i < len - 1; i++) {
        for (int j = 0; j < len - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

**逻辑分析：**

外层循环控制比较的次数，内层循环控制每次比较的元素。若相邻元素逆序，则交换两元素。

**参数说明：**

- `arr`：待排序数组
- `len`：数组长度

### 代码示例：计数排序

void counting_sort(int *arr, int len, int max_value) {
    int count[max_value + 1];
    for (int i = 0; i <= max_value; i++) {
        count[i] = 0;
    }
    for (int i = 0; i < len; i++) {
        count[arr[i]]++;
    }
    int index = 0;
    for (int i = 0; i <= max_value; i++) {
        while (count[i] > 0)